Unit - 4
Turing machines
Q. 1) Write the variants of the Turing machine ?
Ans : Variants of turing machine
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, a method infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
Q. 2) Write short notes on turing machine ?
Ans : Turing machine
A information processing system (TM) may be a mathematical model that consists of
Associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Q. 3) What is the basic model of turing machine ?
Ans : Basic model of turing machine
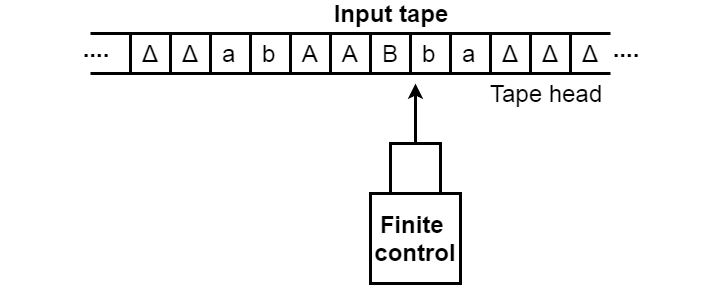
With the help of the following representation, the turning machine can be modelled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
Q. 4) write the closure property ?
Ans : closure property
❖ Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
❖ Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
❖ Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Q. 5) Define nondeterministic TMs ?
Ans : Non- deterministics TM
In a Non-Deterministic computing device, for each state and image, there area unit a
Bunch of actions the thulium will have. So, here the transitions don’t seem to be
Settled. The computation of a non-deterministic computing device could be a tree of
Configurations which will be reached from the beginning configuration.
An input is settle fored if there’s a minimum of one node of the tree that is associate degree accept configuration, otherwise it’s not accepted. If all branches of the machine tree halt on all inputs, the non-deterministic computing device is named a Decider and if for a few inputs, all branches area unit rejected, the input is additionally rejected.
A non-deterministic computing device are often formally outlined as a 6-tuple
(Q, X,∑, δ, q0, B, F) where −
● Q could be a finite set of states
● X is that the tape alphabet
● ∑ is that the input alphabet
● δ could be a transition function;
δ : letter × X → P(Q × X × ).
● q0 is that the initial state
● B is that the blank image
● F is that the set of ultimate states
Q. 6) A turing machine is a
a) real machine
b) abstract machine
c) hypothetical machine
d) more than one option is correct
Ans : correct answer is “ d“
Explanation :
A turing machine is abstract or hypothetical machine thought by mathematician Alan Turing in 1936 capable of simulating any algorithm, however complicated it is.
Q. 7) Write features of turing machine ?
Ans : Various features of turing machine
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Q. 8) Write short notes on Recursively enumerable language ?
Ans : Recursively enumerable
Type-0 grammar produces RE languages or type-0 languages. The Turing machine may accept or recognize a RE language, which means that it will enter the final state for the language strings and may or may not enter the rejecting state for strings that are not part of the language.
It means that for strings that are not a part of the language, TM will loop indefinitely. The languages of RE are often referred to as identifiable Turing languages.
Q. 9) What do you mean by unrestricted grammars ?
Ans : Unrestricted grammars
Recall, a descriptive linguistics is Associate in Nursing abstract entity that makes an
Attempt to explain the “strings” [aka sentences] of a language. As a proper extension
Of a context-free grammar:
Definition: Associate in Nursing unrestricted descriptive linguistics could be a 4-tuple (T,N,P,S), consisting of :
1. T = set of terminals (the legal “tokens” of the language)
2. N = set of nonterminals (aka variables)
3. P = as set of productions, every of the form:
v -> w (what will this mean?)
Where v and w area unit strings consisting of nonterminals and terminals.
4. S = a special nonterminal referred to as the beginning image
This type of descriptive linguistics is additionally referred to as a sort zero descriptive linguistics. It’s such a computing device.
Q. 10) Write short notes on Recursive Language ?
Ans : Recursive Language
Turing machine will determine a recursive language (subset of RE) which means that it will enter the final state for language strings and reject state for strings that are not part of the language.
E.g.; L= {anbncn|n>=1} is recursive since we can create a turing machine that moves to the final state if the string moves to the non-final state of the form anbncn else. So, in this situation, the TM will always halt. The REC languages are often referred to as determinable Turing languages.