Unit - 5

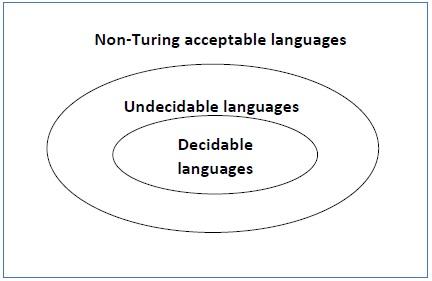
Undecidability

Q. 1) What are the undecidability problems ?

Ans : Undecidability  problems

For an undecidable language, there is no Turing Machine which accepts the

Language and makes a decision for every input string w (TM can make decision for

Some input string though).

A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example

●      The halting problem of Turing machine

●      The mortality problem

●      The mortal matrix problem

●      The Post correspondence problem, etc.

Q. 2) What is the church - turing thesis ?

Ans : church - turing thesis

In 1936, a technique named as lambda-calculus was created by Alonzo Church

Within which the Church numerals area unit well outlined, i.e. the encryption of

Natural numbers. Additionally in 1936, mathematician machines (earlier known as

Theoretical model for machines) was created by mathematician, that’s used for

Manipulating the symbols of string with the assistance of tape.

Church - Turing Thesis :

Turing machine is outlined as associate degree abstract illustration of a computer

Like hardware in computers. Mathematician planned Logical Computing Machines

(LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to

Outline algorithms properly. So, Church created a mechanical methodology named

As ‘M’ for manipulation of strings by mistreatment logic and arithmetic.

This methodology M should pass the subsequent statements:

• Number of directions in M should be finite.

• Output ought to be made when playing a finite variety of steps.

• It mustn’t be imagined, i.e. is created in the world.

• It mustn’t need any complicated understanding.

Using these statements Church planned a hypothesis known as Church’s

Mathematician thesis that may be expressed as: “The assumption that the intuitive

Notion of estimable functions is known with partial algorithmic functions.”

In 1930, this statement was initial developed by Alonzo Church and is typically

Brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis

Can not be proved .

The algorithmic functions is estimable when taking following assumptions:

1. Every and each operate should be estimable.

2. Let ‘F’ be the estimable operation and when playing some elementary operations to ‘F’, it’ll rework a replacement operation ‘G’ then this operate ‘G’ mechanically becomes the estimable operation.

3. If any operates that follow on top of 2 assumptions should be states as

Estimable function.

Q. 3) What do you mean by halting problem of turing machine ?

Ans : Halting problem

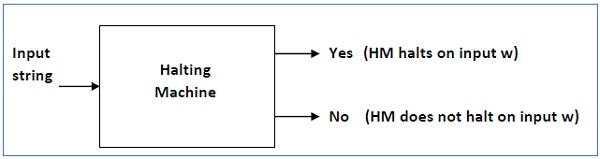
Input : A machine with Turing and an input string w.

Problem : Does the Turing machine complete the w-string computation in a finite number of steps? Either yes or no must be the answer.

Proof : We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or 'no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as 'no'.

The Halting Computer block diagram is as follows.

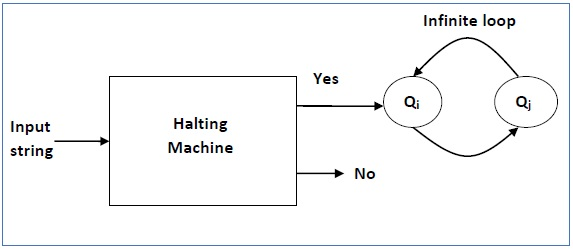
We're now going to build an inverted stopping machine (HM)' as -

●      If H returns YES, then loop forever.

●      If H returns NO, then halt.

The following is a 'Inverted Stopping Unit' block diagram -

In addition, as follows, a machine (HM)2 whose input itself is constructed

●      If (HM)2 halts on input, loop forever.

●      Else, halt.

We have a contradiction here. The stopping question is therefore undecidable.

Q. 4) Explain Rice’s theorem ?

Ans : Rice’s theorem

Rice theorem states that any non-trivial linguistics property of a language that is

Recognized by a information processing system is undecidable. A property, P, is that

The language of all Alan Mathison Turing machines that satisfy that property.

Formal Definition

If P may be a non-trivial property, and therefore the language holding the property,

Lp , is recognized by information processing system M, then record = L(M) ∈ P is

Undecidable.

Description and Properties

• Property of languages, P, is solely a collection of languages. If any language

Belongs to P (L ∈ P), it's aforesaid that L satisfies the property P.

• A property is named to be trivial if either it's not happy by any recursively

Numerable languages, or if it’s happy by all recursively numerable languages.

• A non-trivial property is happy by some recursively numerable languages and

Aren’t happy by others. Formally speaking, in an exceedingly non-trivial property,

Wherever L ∈ P, each the subsequent properties hold:

o Property one one There exists Alan Mathison Turing Machines, M1 and M2

That acknowledge constant language, i.e. either ( , ∈ L ) or ( , ∉ L )

o Property two two There exists Alan Mathison Turing Machines M1 and M2,

Wherever M1 acknowledges the language whereas M2 doesn’t, i.e. ∈ L and ∉ L

Proof

Suppose, a property P is non-trivial and φ ∈ P.

Since, P is non-trivial, a minimum of one language satisfies P, i.e., L(M0) ∈ P , ∋

Information processing system M0.

Let, w be associate degree input in an exceedingly specific instant and N may be a

Information processing system that follows −

On input x

●      Run M on w

●      If M doesn’t settle for (or does not halt), then don't settle for x (or don’t halt)

●      If M accepts w then run M0 on x. If M0 accepts x, then settle for x.

A perform that maps associate degree instance ATM = M accepts input w to a N such

●      If M accepts w and N accepts constant language as M0, Then L(M) = L(M0) ∈ p

●      If M doesn’t settle for w and N accepts φ, Then L(N) = φ ∉ p

Since ATM is undecidable and it is reduced to record, record is additionally undecidable.

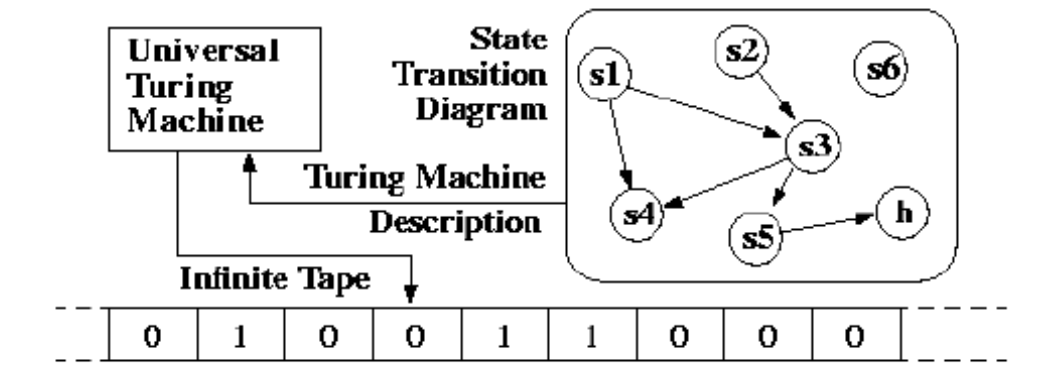
Q. 5) Describe a universal turing machine ?

Ans : universal turing machine

A Turing Machine is the mathematical tool equivalent to a digital computer. It was

Suggested by the mathematician Turing in the 30s, and has been since then the

Most widely used model of computation in computability and complexity theory.

The model consists of an input output relation that the machine computes. The input

Is given in binary form on the machine’s tape, and the output consists of the contents

Of the tape when the machine halts.

What determines how the contents of the tape change is a finite state machine (or

FSM, also called a finite automaton) inside the Turing Machine. The FSM is

Determined by the number of states it has, and the transitions between them.

At every step, the current state and the character read on the tape determine the

Next state the FSM will be in, the character that the machine will output on the tape

(possibly the one read, leaving the contents unchanged), and which direction the

Head moves in, left or right.

The problem with Turing Machines is that a different one must be constructed for

Every new computation to be performed, for every input output relation.

This is why we introduce the notion of a universal turing machine (UTM), which

Along with the input on the tape, takes in the description of a machine M. The UTM

Can go on then to simulate M on the rest of the contents of the input tape. A universal turing machine can thus simulate any other machine.

Q. 6) Which of the following is/are undecidable?

A. 3 only

B. 3 and 4 only

C. 1, 2 and 3 only

D. 2 and 3 only

Ans :  correct answer is “D” .

Explanation : 

1. Option 1 is whether or not a CFG is null, and that question can be determined.

2.     Option 2 is whether all possible strings (everything or completeness of CFG) are generated by a CFG; this problem is undecidable.

3.     Option 3 is whether it is undecidable if the language generated by TM is regular.

4.     Option 4 is to decide if the language produced by the DFA and the NFA is the same. So choice D is correct.

Q. 7) Take three decision problems into account: P1, P2 and P3. P1 is considered to be decidable and P2 to be undecidable. That is Valid for one of the following?

A. P3 is undecidable if P2 is reducible to P3

B. P3 is decidable if P3 is reducible to P2’s complement

C. P3 is undecidable if P3 is reducible to P2

D. P3 is decidable if P1 is reducible to P3

Ans : correct answer is “ A” .

Explanation :

1. Option A suggests P2-P3. If P2 is undecidable, then P3 is undecidable, according to theorem 2 discussed. It is considered that P2 is undecidable, so P3 would be undecidable as well. So choice (A) is true.

2.     Choice (B) indicates P3-P2 '. If P3 is undecidable, then P2 is undecidable, according to theorem 2 discussed. The undecidability of P3 is not, however, in doubt. So choice (B) is incorrect.

3.     Option C says P3-P2.  If P3 is undecidable, then P2 is undecidable, according to theorem 2 discussed. The undecidability of P3 is not, however, in question.

4.     P1-P3 says Option D. If P3 is decidable, then P1 is also decidable, according to the theorem 1 discussed. But the determinability of P3 is not in doubt. So choice (D) is inaccurate.

Q. 8) According to the rice’s theorem, If P is a non trivial property, Lp is :

a) infinite

b) decidable

c) undecidable

d) none of the mentioned

Ans : correct answer is “C” .

Explanation :

Rice’s theorem states that ‘Any non trivial property about the language recognized by a turing machine is undecidable’.

Q. 9) Diagonalization can be useful in:

a) To find a non recursively enumerable language

b) To prove undecidability of halting problem

c) Both (a) and (b)

d) None of the mentioned

Ans : correct answer is “ C “.

Explanation :

Diagonalization is a technique we use for the following operations:

a) To find a non recursively enumerable language.

b) To prove undecidability of halting problem.

Q. 10) What do you mean by decidable issue and undecidable issue , explain with example ?

Ans : Decidable issue

A problem is decidable if we will construct a information processing system which

Can halt in finite quantity of your time for each input and provides answer as ‘yes’ or

‘no’. A decidable downside has associate degree formula to work out the solution for

a given input.

Examples

• Equivalence of 2 regular languages: Given 2 regular languages, there’s

Associate degree formula and information processing system to make a decision

Whether or not 2 regular languages ar equal or not.

• Finiteness of normal language: Given an everyday language, there’s

Associate degree formula and information processing system to make a decision

Whether or not regular language is finite or not.

• Emptiness of context free language: Given a context free language, there’s

Associate degree formula whether or not CFL is empty or not.

Undecidable issues

A problem is undecidable if there’s no information processing system which can

Continuously halt in finite quantity of your time to provide answer as ‘yes’ or ‘no’.

Associate degree undecidable downside has no formula to work out the solution for a

Given input.

Examples

• Ambiguity of context-free languages: Given a context-free language, there’s

No information processing system which can continuously halt in finite quantity of

Your time and provides answer whether or not language is ambiguous or not.

• Equivalence of 2 context-free languages: Given 2 context-free languages,

There’s no information processing system which can continuously halt in finite

Quantity of your time and provides answer whether or not 2 context free languages ar

Equal or not.

• Everything or completeness of CFG: Given a CFG and input alphabet,

Whether or not CFG can generate all doable strings of input alphabet (∑*)is

Undecidable.

• Regularity of CFL, CSL, REC and REC: Given a CFL, CSL, REC or REC,

Determinative whether or not this language is regular is undecidable.