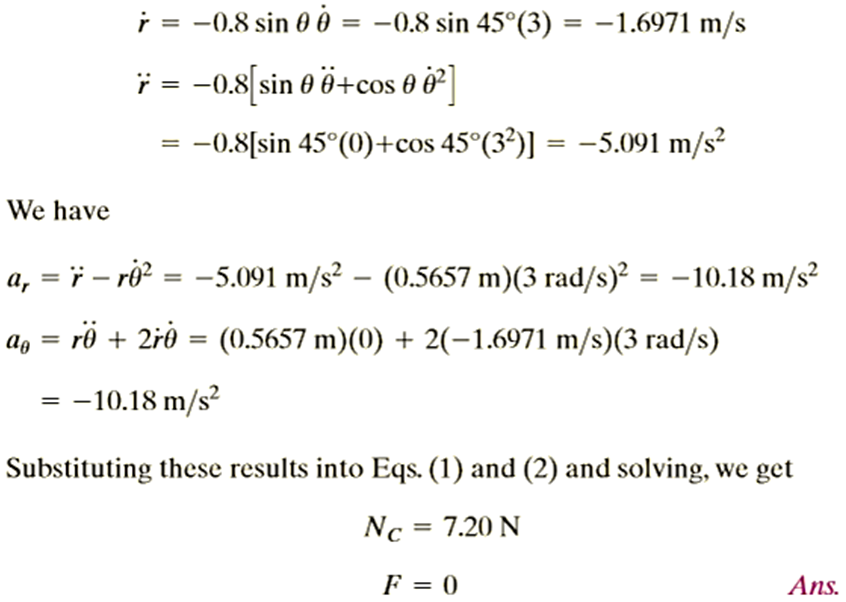Unit 4

Dynamics

Q1. Define and classify dynamics

Solution: Dynamics is the branch of mechanics that deals with the motion of the particle or a rigid body. In other words, dynamics deals with the accelerated motion of a body. Analysis in dynamics involves motion. Dynamics can be sub-divided into two parts:

Kinematics is the branch of mechanics or simply a part of dynamic analysis which deals with the study or analysis of the motion of the body without considering the forces that causes this motion.

Hence Kinematics only analyses the geometry of the particle or rigid body.

2.     Kinetics

Kinetics is the branch of mechanics or simply a part of dynamic analysis which deals with the study of motion of the body by considering the forces that causes this motion.

In other words, kinematics relates with the forces acting on the moving body.

Dynamics can be also classified on the basis of the body under study.

Particle is nothing but a point body or a body who does not have any size and shape. Analysis of a particle in motion is referred to as particle dynamics

2.     Rigid body dynamics

Rigid body is a body who does not change its shape and size when subjected to various forces and couples. Analysis of rigid body is referred to as rigid body dynamics

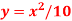Q2. At any instant the horizontal position of the weather balloon is defined by where t is in seconds and x is in meters. If the equation of the path of the balloon is . Determine the magnitude and direction of the velocity and the acceleration when t = 2 s.

Solution:

Velocity:

The velocity component in the x direction is

At t = 2 s

The velocity component in the y direction is

At t = 2 s

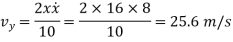
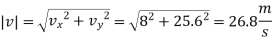
The direction is tangent to the path

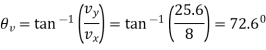
Acceleration:

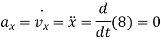
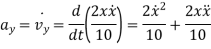
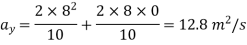
Magnitude of acceleration is

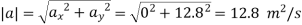
Direction of acceleration is

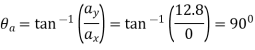
Q3. For a short time, the path of the plane is described by If the plane is rising with a constant velocity of 10 m/s, determine the magnitudes of the velocity and acceleration of the plane when it is at y = 100 m

Solution:

Q4. A race car C travels around the horizontal circular track that has a radius of 300 ft. If the car increases its speed at a constant rate of 7 ft/s2 starting from rest, determine the time needed for it to reach an acceleration of 8 ft/s2. What is its speed at this instant?

Solution:

Q5. The amusement park ride shown in Fig below consists of a chair that is rotating in a horizontal circular path of radius r such that the arm OB has an angular velocity and angular acceleration . Determine the radial and transverse components of velocity and acceleration of the passenger. Neglect his size in the calculation.

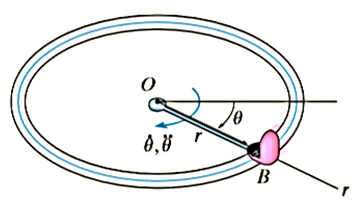
Solution:

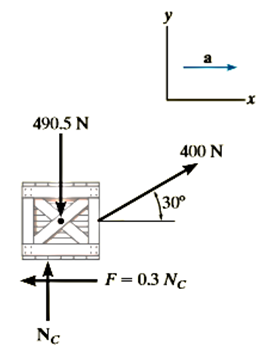
Q6. The 50-kg crate shown in Fig below rests on a horizontal surface for which the coefficient of kinetic friction 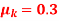is If the crate is subjected to a 400-N towing force as shown, determine the velocity of the crate in 3 s starting from rest.

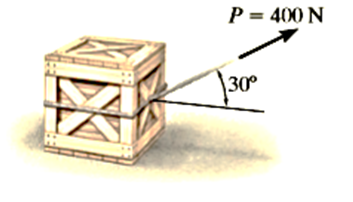
Solution

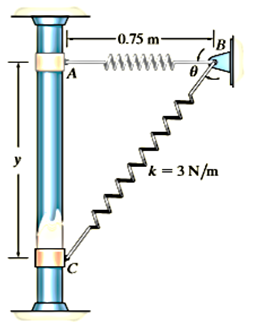
Q7. A smooth 2-kg collar C, shown in Fig, is attached to a spring having a stiffness k = 3 N/m and an unstretched length of 0.75 m. If the collar is released from rest at A, determine its acceleration and the normal force of the rod on the collar at the instant y = 1 m

Solution:

Q8. Determine the banking angle for the race track so that the wheels of the racing cars will not have to depend upon friction to prevent any car from sliding up or down the track. Assume the cars have negligible size, a mass m, and travel around the curve of radius with a constant speed v.

Solution:

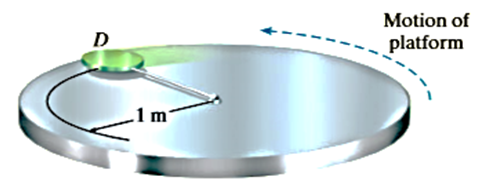
Q9. The 3-kg disk D is attached to the end of a cord as shown in Fig. The other end of the cord is attached to a ball-and-socket joint located at the center of a platform. If the platform rotates rapidly, and the disk is placed on it and released from rest as shown, determine the time it takes for the disk to reach a speed great enough to break the cord. The maximum tension the cord can sustain is 100 N, and the coefficient of kinetic friction between the disk and the platform is

Solution:

Q10. The smooth 0.5-kg double-collar can freely slide on arm AB and the circular guide rod. If the arm rotates with a constant angular velocity of , determine the force the arm exerts on the collar at the instant 450. Motion is in the horizontal plane.

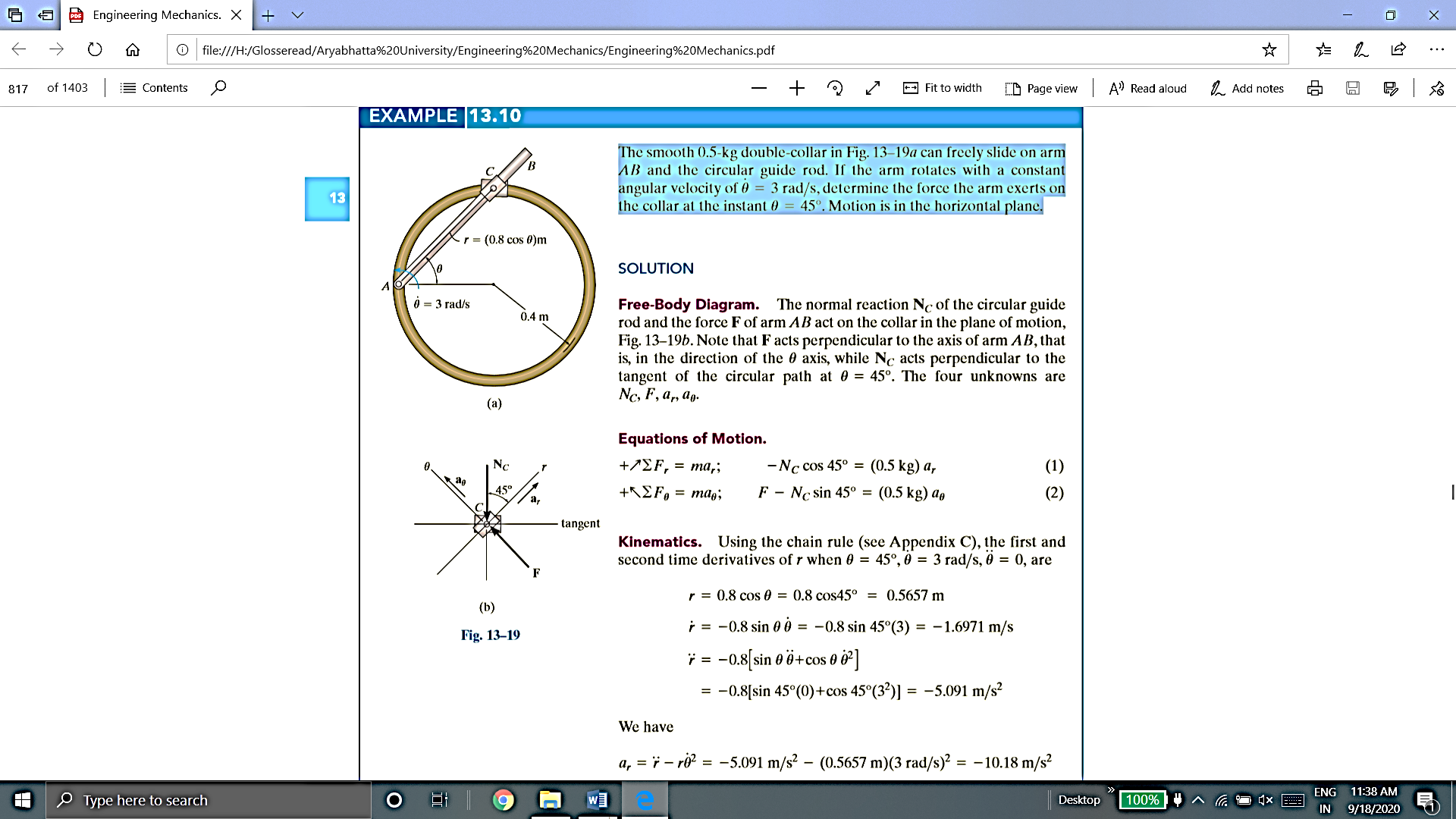
Solution: