Unit-1

Fluids

Q1) Define fluid and its type.

A1: A fluid is a substance which is capable of flowing under the action of shear force (however small force may be).

Example- Liquid, gases, vapour.

For a static fluid, shear force is zero.

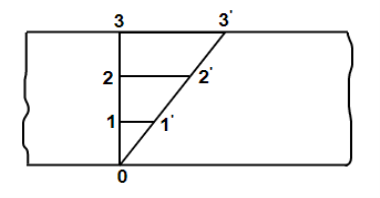
Figure 1: Force at static fluid

Solid regains their original shape if the shear force within elastic limit when the force is removed. But fluid never regains original shape after the removal of force.

There are two types of fluid:

Q2) Explain Newton’s law of viscosity.

A2: According to Newton’s law of viscosity the shear stress is directly proportional to rate of shear strain or rate of angular deformation or velocity gradient. The fluid which follows this is law is called newtonion fluid.

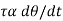
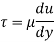
Newton’s law of viscosity is similar to hooke’s law for solid.

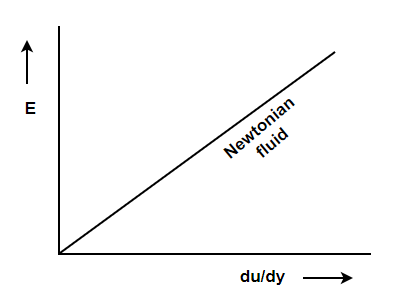
Figure 2: Diagram for Newton’s law of viscosity

Q3) Define the following terms:

A3:

It is defined as the ratio of mass of the fluid to its volume. Its unit is     kg/m3 and its dimensional formula is ML-3.

Density depends on temperature and pressure.

2.     Specific Volume:

Specific volume is defined as the ratio of volume of fluid to the mass of fluid.

It is denoted by Vs.

Mathematically it is denoted as

Vs=V/m=1/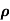

3.     Specific Gravity:

It is defined as the ratio of density of fluid to the density of standard fluid.

Or

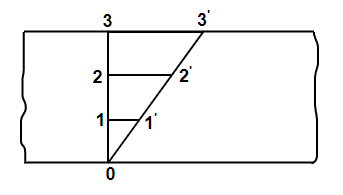
Q4)  Explain Viscosity and derive its formula.

A4: Viscosity is a measure of a fluid's resistance to flow. It describes the internal friction of a moving fluid. A fluid with large viscosity resists motion because its molecular makeup gives it a lot of internal friction. It is the internal resistance offered by one layer fluid to the other layer.

Figure 3: Viscosity diagram

V=d/t

D=v.t

d =du.dt

tandθ=(du.dt)/dy

As the tandθ is very less, then

                                                                   tandθ=dθ

then,                                                             dθ=(du.dt)/dy

dθ/dt=du/dy

we know that,    shear stress= shear force/shear area

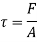
As the molecules are taken into same area:

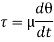
Q5)

A flat plate of area is pulled with a speed of 0.4m/s relative to another plate located at a distance of 0.15mm from it. Find the force and power required to maintain this speed. If the fluid separating them is having viscosity as 1 poise.

A5)

Area of plate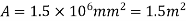

Speed of plate relative to another plate,

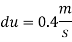
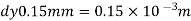
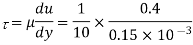
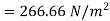
(i) Shear force

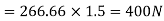
(ii)

Power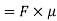

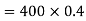
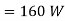
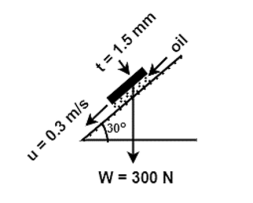
Q6) Calculate the dynamic viscosity of an oil, which is used for lubrication between a square plate of size 0.8m×0.8m and an inclined plane with angle of inclination 30o as shown in figure. The weight of square plate is 200N and it slides down the inclined plane with a uniform velocity of 0.3 m/s. The thickness of oil film is 1.5mm.

A6)

A=0.8m×0.8m

𝛉 =30o

W=300N

U=0.3 m/s

Component of weight W, along the plane

=W cos 60o

=300 cos 60o

F=150 N

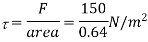
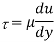
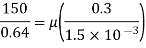
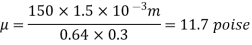
Q7)

Find the kinematic viscosity of an oil having density 981kg/m3. The shear stress at a point in oil is 0.2452 N/m2 and velocity gradient at that point is 0.2 per second.

A7)

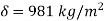
=0.2452 N/m2

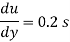
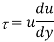
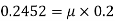
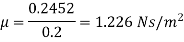
kinematic viscosity

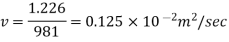
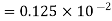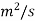
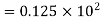×c

c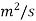

Q8) Define Surface tension.

A8:

“Surface tension is the tension of the surface film of a liquid caused by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimise surface area”.

Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible. Surface tension allows insects (e.g. water striders), to float and slide on a water surface without becoming even partly submerged.

At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).

There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane.

Because of the relatively high attraction of water molecules to each other through a web of hydrogen bonds, water has a higher surface tension (72.8 milli newtons (mN) per meter at 20 °C) than most other liquids. Surface tension is an important factor in the phenomenon of capillarity.

Surface tension has the dimension of force per unit length, or of energy per unit area. The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.

In materials science, surface tension is used for either surface stress or surface energy.

Formula for surface tension

Where,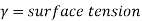

L=Length

F= force

S.I. Unit of Surface tension is N/m

The dimensional formula of surface tension is MT-2.

Q9)  Explain capillarity.

A9) Capillarity:

It is the rise or depression of a liquid in a small passage such as a tube of small cross-sectional area, like the spaces between the fibres of a towel or the openings in a porous material.

Capillary action occurs when the adhesion to the walls is stronger than the cohesive forces between the liquid molecules. The height to which capillary action will take water in a uniform circular tube (picture to right) is limited by surface tension and, of course, gravity.

A tube of very fine bore is called capillary. The phenomenon of rise or fall of a liquid in a capillary tube is called capillarity.

If we consider meniscus to be hemispherical in shape, the weight of the liquid rise (the total upward force) = (Volume of liquid in cylinder upto h + volume of liquid in cylinder of radius r and height r – volume of hemisphere of radius r) ρg.

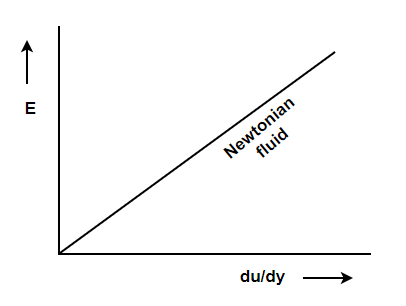
Figure 4: Capillarity phenomenon

2πr×Tcosθ=[πr2×h+πr2×r−23πr3]ρg2πr×Tcosθ=[πr2×h+πr2×r-23πr3]ρg 

T=r(h+r3)ρg2cosθT=r(h+r3)ρg2cosθ.

For capillary r3r3 can be neglected h=2Tcosθrρgh= 2Tcosθrρg.

This is called Ascent formula.

Q10) Explain Compressibility and Bulk Modulus.

A10: It is reciprocal of Bulk modulus (K)

ß=1/K

Bulk Modulus is defined as the ratio of compressive stress to volumetric strain.

K=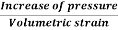

K=(dp)/(-dv/V)

-ve sign means the volume decrease with increase in pressure.

We know that,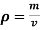                                   

Since, R= Characteristics gas constant and T is constant (isothermal process).

Differentiating the above equation      (dp/d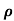)= RT

Now the isothermal bulk modulus

KT=.(dp/d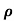)= 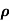. RT=P

KT=P