Unit 1
Heat Conduction
Q1. Given: A jet aircraft compartment is assumed to be a cylindrical tube of 3-m diameter and 20-m length. It is lined inside with 3 cm of insulating material of k = 0.042 W/mK. It is flying at a height where the average outside temperature is – 30°C. To find: The rate of heating required to maintain the compartment at 20°C for passenger comfort.
Ans:

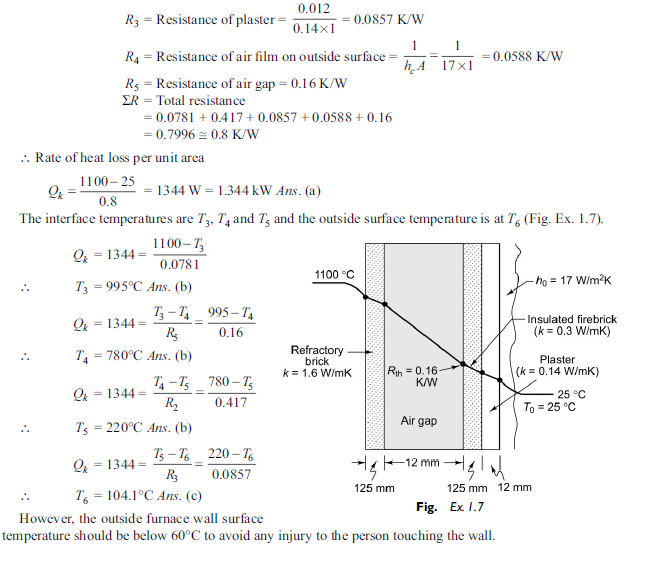
Q2. Given: A furnace wall has the inside surface temperature of 1100°C, while the ambient air temperature is 25°C. The wall consists of 125 mm thick refractory bricks (k = 1.6 W/mK), 125 mm thick firebricks (k = 0.3 W/mK) and 12 mm thick plaster (k = 0.14 W/mK). There is an air gap which offers a thermal resistance of 0.16 K/W. The heat transfer coefficient on the outside wall to the air is 17 W/m2K. To find: (a) The rate of heat loss per unit area of wall surface, (b) the interface temperatures throughout the wall, and (c) the temperature of the outside surface of the wall.

Q3. Given: A plastic pipe (k = 0.5 W/mK) of inner diameter 3 cm and outer diameter 4 cm carries a fluid of average temperature 100°C and h = 300 W/m2K. The rate of heat transfer per unit length is 500 W/m.
To find: (i) The outside surface temperature of pipe, (ii) the overall heat transfer coefficient based on outside area.

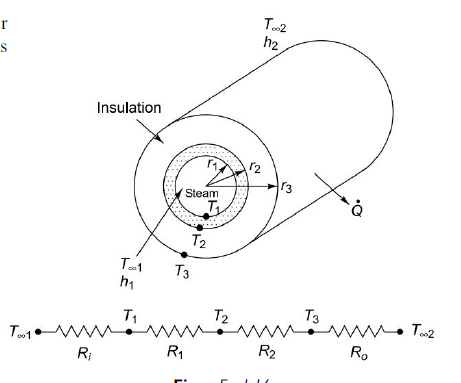
Q4. Given: Steam at 350°C flowing in a pipe (k = 80 W/mK) 5 cm inner diameter 5.6 cm outer diameter is covered with 3 cm thick insulation (k = 0.05 W/mK). Heat is lost to the surroundings at 5°C by natural convection and radiation with combined h = 20 W/m2K and hi = 60 W/m2K.
To find: (i) The rate of heat loss from the pipe per unit length, (ii) the temperature drops across the pipe and the insulation.

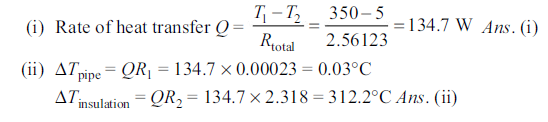
Q5. Given: A pipe 2 cm in dia. at 40°C is placed in (i) an air flow at 50°C, with h = 20 W/m2K and in (ii) water at 30°C with h = 70 W/m2K.
To find: The heat transfer rate per unit length of the pipe.

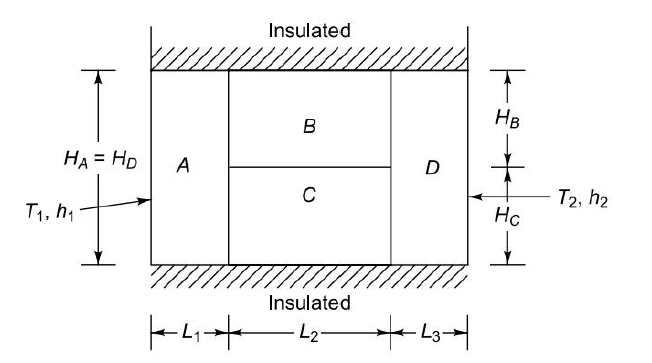
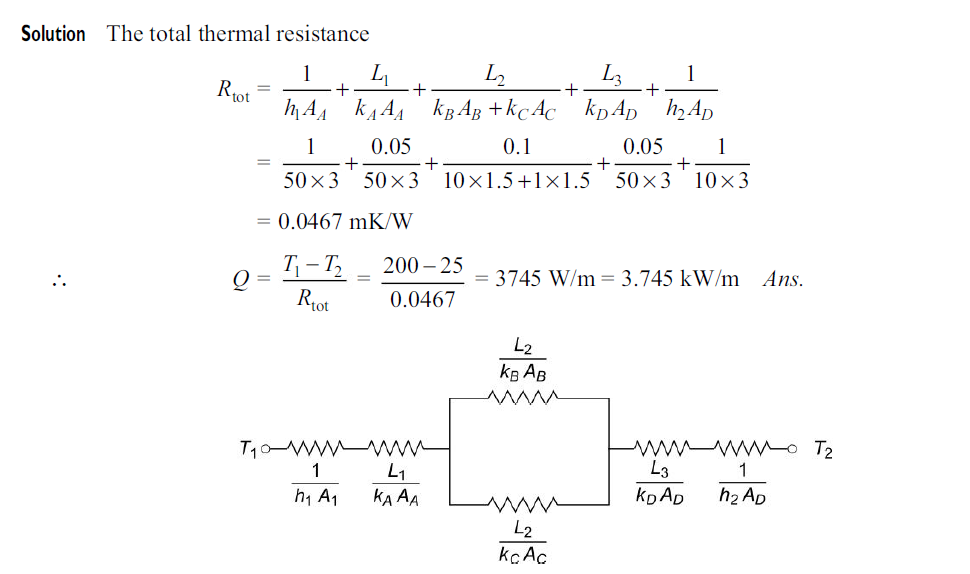
Q6. Given: The composite wall having unit length normal to the plane of paper and the equivalent thermal circuit are shown in Figure
HA = HD = 3 m, HB = HC = 1.5 m
L1 = L3 = 0.05 m, L2 = 0.1 m
KA = kD = 50 W/mK, kB = 10 W/mK, kC = 1 W/mK
T1 = 200ºC, h1= 50 W/m2 K, T2 = 25ºC, h2 = 10 W/m2K.
To find: The rate of heat transfer through the wall.
Q7. A stainless steel fin (k = 20 W/m K) having a diameter of 20 mm and a length of 0.1 m is attached to a wall at 300°C. The ambient temperature is 50°C and the heat transfer coefficient is 10 W/m2 K. The fin tip is insulated.
Determine (a) the rate of heat dissipation from the fi n, (b) the temperature at the fi n tip, (c) the rate of heat transfer from the wall area covered by the fi n if the fi n was not used and (d) the heat transfer rate from the same fin geometry if the stainless steel fin is replaced by a fictitious fin with infinite thermal conductivity.
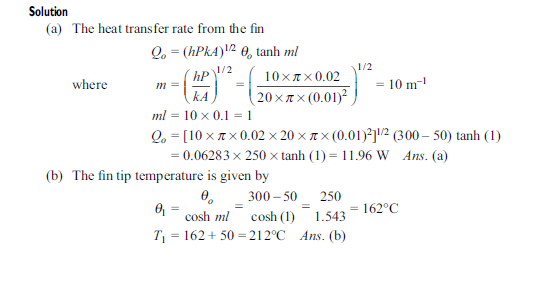

Q8. A copper fin (k = 396 W/mK) 0.25 cm in diameter protrudes from a wall at 95°C into ambient air at 25°C. The heat transfer coefficient by free convection is equal to 10 W/m2K. Calculate the heat loss if (a) the fin is infinitely long, (b) the fin is 2.5 cm long and the coefficient at the end is the same as around the circumference.
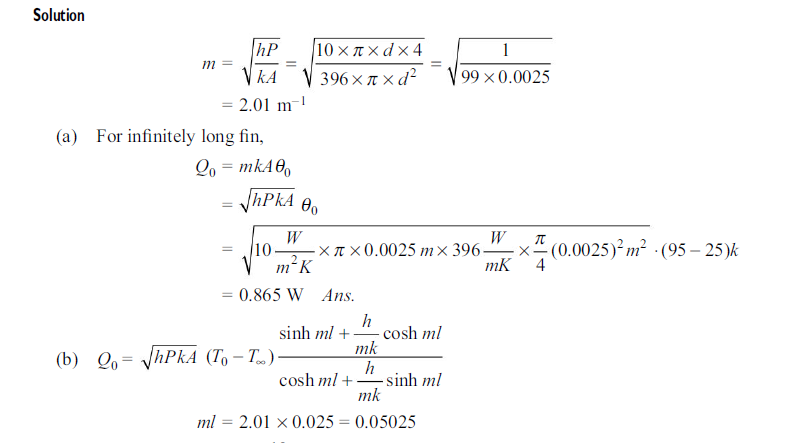
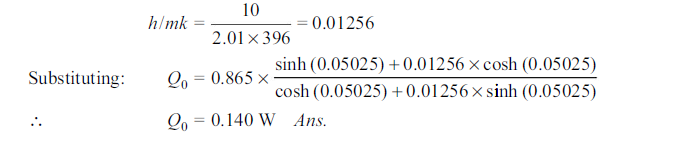
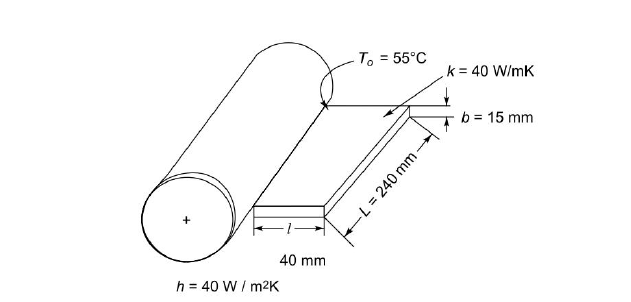
Q9. The body of an electric motor is 360 mm in diameter and 240 mm long. It dissipates 360 W of heat and its surface temperature should not exceed 55°C. Longitudinal fi ns of 15 mm thickness and 40 mm height are proposed. The heat transfer coefficient is 40 W/m2 K when the ambient air is 30°C. Determine the number of fins required, if k of the fin material is 40 W/mK.
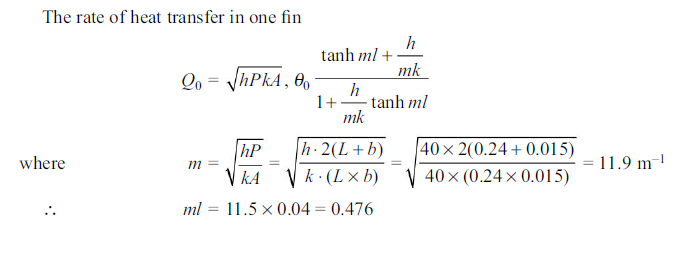

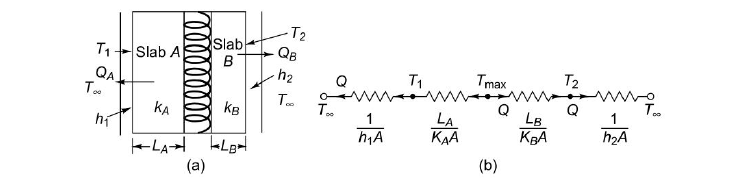
Q10. A square plate 1 kW electric heater (150 mm x 150 mm) is inserted between two slabs. Slab A is 20 mm thick (k = 50 W/mK) and slab B is 10 mm thick (k = 0.2 W/mK). The outside heat transfer coefficients on side A and side B are 200 W/m2 K and 50 W/m2 K respectively. The temperature of surrounding air is 25°C.
Estimate (a) the maximum temperature in the system and (b) the outside surface temperatures of the two slabs. Draw the equivalent electrical circuit.
LA = 0.02 m, LB = 0.01 m,
KA= 50 W/mK, kB = 0.2 W/mK, h1 = 200 W/m2K,
H1 = 50 W/m2 K,  = 25°C
= 25°C