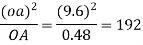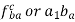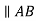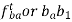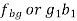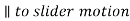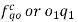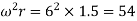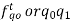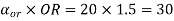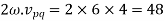Unit 2
Kinematic analysis of plane mechanism
Q1. Define relative velocity and describe the relative velocity method to determine the velocity of four bar mechanism.
A1:
Relative velocity: Relative velocity can be defined as the comparative velocity of two moving bodies with different or same velocity. Let us assume the va and vb be the velocity of body A and B respectively. Relative velocity of body A with respect to the body B is given by:
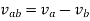
Similarly, relative velocity of body b with respect to body a is given by:
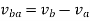
Relative velocity method
Let us consider a four-link mechanism shown in figure , in which link AB is be the driver which is rotating with an angular velocity , link AD is fixed, link BC be the coupler and the link CD be the driven or output link, whose velocity can be obtained as follows:
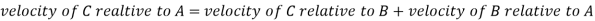
As the link AD is fixed so in order to obtain the absolute velocity of any point on the mechanism can be obtained relative to any point on the link AD. That’s why the velocity of C relative to A is equal to velocity of C relative to D
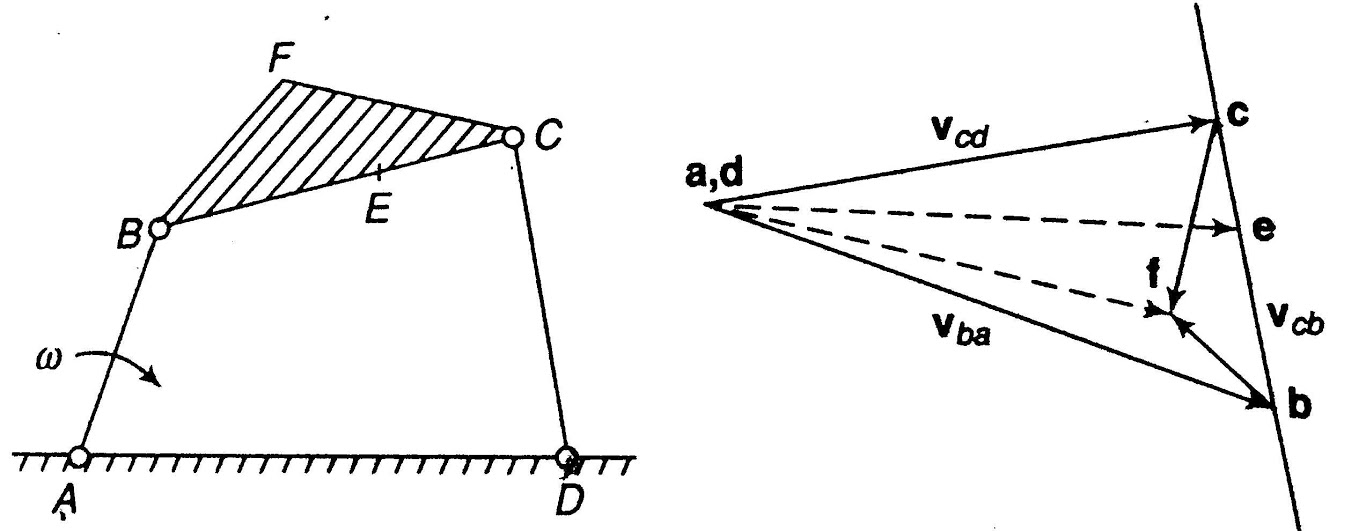
Figure. Four bar mechanism and its velocity diagram
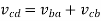
From the velocity diagram
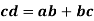
Where 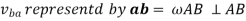
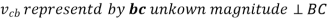
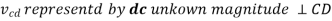
In order to obtain the unknown velocities velocity diagram with a given scale is to be made. Steps to draw the velocity diagram are as follows:
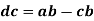

Velocity of intermediate points
The velocity of any intermediate point can be obtained by dividing the velocity vector in the ratio same as the point divides the link. velocity of point E relative to B on the link BC is represented by be and can be obtained as follows:
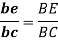
Velocity of offset points
In figure 2, point F be the offset point on the link BCF. In order to obtain the velocity of point F, construct a line perpendicular to link BC through point b in velocity diagram and another line perpendicular to BC through point c. the intersection point of these two perpendicular lines will provide the point f, as shown in figure. By joining the point f and a/d we can obtain the absolute velocity of the offset point f, which is represented by the vector af or df.
Vector equation for the point F is given as follows:
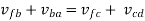

Q2. Discuss about the velocity of rubbing.
A2: Figure given below shows the ends of two links of a turning pair, which consists of two parts one is pin and other is hole. During operation hole of one link will rub on the surface of pin of the other link. Such relative motion between the pin surface and the hole is known as rubbing velocity, it can be calculated by the obtaining the algebraic some of angular velocities of the connecting links multiplied by the radius of pin.
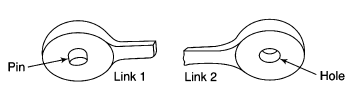
Ends of two links of a turning pair
Consider a turning pair shown in figure of turning pair connected by pin joint, in which link OA and OB are connected by a pin joint having angular velocity 1 and 2 respectively and r be the radius of pin. The rubbing velocity of the pin joint is given by
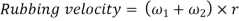
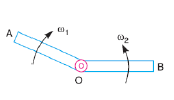
Turning pair connected by pin joint
If the links are rotating in same direction, rubbing velocity is given by:
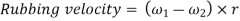
In case when the pin joint connects a sliding member to a turning member, angular velocity of sliding link is taken as 0. Let us assume in such pair be the angular velocity of the turning link and r be the radius of pin, then
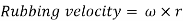
Q3. Discuss the relative velocity approach to find the velocity of a slider crank mechanism at different locations.
A3.
Consider figure given below in which the link OA is the crank which is rotating with an angular velocity of rad/sec, link B is sliding on the fixed guide G and Ab be the coupler link. if we have to find the velocity of the slider, we can follow the given steps

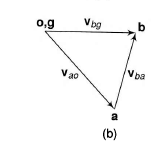
(a) Slider crank mechanism (b) velocity diagram of slider crank mechanism
Step 1: Draw the velocity diagram see figure (b).
To draw the vector diagram first of all, draw a vector oa (denoted by vao) perpendicular to the link OA with a suitable scale.
Link OG is fixed hence the vector og is a point vector without any length.
Now draw a line perpendicular to link AB and another line representing the motion of slider in horizontal direction from point og.
Intersection of the line perpendicular to the link AB and horizontal line representing the motion of slider gives the point b.
Now we get the vectors bg (denoted by vbg) and ab (denoted by vba) the length of these vectors represents the velocities of link AB and the slider at B.
Step 2: Write the vector equation for the velocity
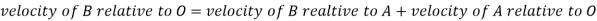
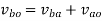
From figure (b)
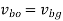

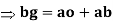
Step 3: Now convert the obtained vectors using the scale selected for drawing velocity diagram.
bg represents the velocity of B relative to O.
ao represents the velocity of A relative to O.
ab represents the velocity of A relative to B.
Angular velocity of coupler link can be obtained by:
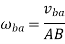
Q4. In the mechanism shown in Figure the piston D moves in the vertical direction upwards with a velocity of 5 m/s. O1A = 7.5 cm, O1O2 = 30 cm, AB=25 cm, O2C = O2B = 10 cm, CD = 25 cm, and BC =12.5 cm. Find the speed in rpm and direction of rotation of crank O1A.
A4.
Draw the configuration diagram with a given suitable scale e.g. in this case scale is taken as 1cm = 5cm shown in figure a.
Now let us assume that link O1A is rotating in clockwise direction and the velocity of point a i.e. va is plotted as 5cm on a scale.
Now draw the velocity diagram Shown in figure b as follows:
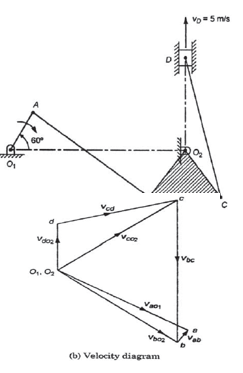
1. Draw va= o a ⊥ O1A, o1a = 5cm.
2. Draw ab ⊥ AB and o2b ⊥O2B meeting at point b.
3. Draw bc ⊥ BC and o2c ⊥ O2C meeting at point c.
4. Draw o2d ⊥ O2D and cd ∥ CD meeting at point d.
Now by measurement
o2d = 2 cm represents the vd which is equal to 5m/s.
for our scale 1 cm = 2.5 m/s.
And va =2.5×5= 12.5 m/s.
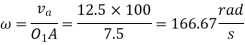

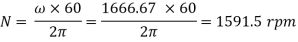
Q5. Define instantaneous center and discuss its properties.
A5. Instantaneous center can be defined as a point about which link can be considered to be rotating at a given instant. Such a center has zero velocity, i.e. the link is at rest at this point. This center varies from instant to instant for different positions of the link. The locus of these centers is termed the centrode. Number of instantaneous centers for a mechanism can be calculated as follows:

Where N is the number of instantaneous centers and n be the number of links in the mechanism.
Properties of Instantaneous Center
Q6. What are the different types of instantaneous centers? Discuss about each of them in brief.
A6. There are three types of instantaneous centers for any mechanism. Figure given below illustrates all the types of instantaneous centers, in which the instantaneous centers 12 and 14 does not move from its position because one link among the two links for the given instantaneous center is fixed, hence these instantaneous centers are termed as the fixed instantaneous centers.
Instantaneous centers 23 and 34 always remains at the at the intersection of the given links hence they may change their position as the links moves but their position on the links is permanent hence, these instantaneous centers are known as permanent instantaneous centers.
Instantaneous centers 13 and 24 changes their position in space with the configuration of mechanism and they also does not lie on any permanent position on the links, hence they are neither permanent nor fixed.
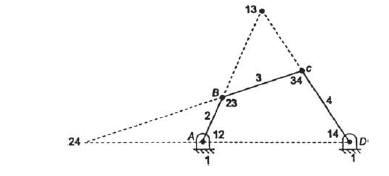
Instanteneous centers of four bar mechanism
Q6. Define the Arnold Kennedy’s theorem to locate instantaneous centers.
A6. According this theorem instantaneous centers of three -plane bodies in relative motion to each other must be co-linear.
Let us consider three links 1,2 and 3 as shown in figure given below. In the given diagram link 1 is fixed while links 2 and 3 are movable. Instantaneous center of link 1,2 and 1,3 lies on the pin joint at 12 and 13 as shown in figure 8. Now let us consider the instantaneous center for the link 2 and 3 in not co-linear to 12 and 13. In this case point 23 have two different direction of motion which is not possible. The one direction of motion for the point 23 is possible only if it is colinear to 12 and 13. That is what Kennedy’s theorem says.
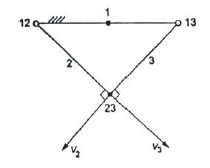
Proving Kennedy theorem
Method to Locate Instantaneous Centers
To locate instantaneous center for a mechanism we have to follow following steps:
Step 1: Determination of number of instantaneous centers N by using relation discussed above. Let us consider the number of links for the given mechanism is 4 shown in figure given below.
Therefore,
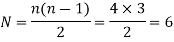
Step 2: Make a list of all the instantaneous centers as follows:
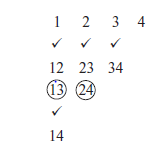
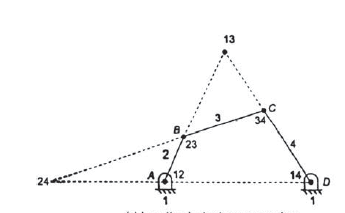
Instantaneous centers for a four-bar mechanism
Step 3: Locate the fixed and permanent instantaneous centers using tick mark by inspection.
Step 4: Now to locate neither fixed nor permanent instantaneous centers use Kennedy’s theorem.
Now apply Kennedy’s theorem here links 1,2 and 3 are in relative motion hence the instantaneous center 13 can be obtained by joining the lines extending the obtained by joining instantaneous centers 12, 23 and 14, 34. Similarly links 1,2 and 4 are in relative motion and the instantaneous center 24 can be obtained at the intersection of the lines joining the instantaneous centers 23,34 and 12,14.
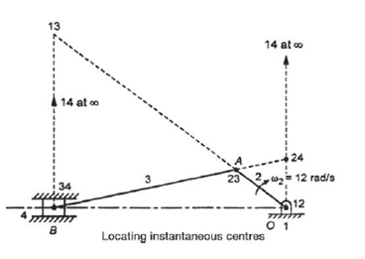
Q7. Locate the instantaneous centers of the slider crank mechanism shown in figure. Find the velocity of the slider.
OA = 160 mm, AB = 470 mm, and OB = 600 mm, 2 = 12 rad/s cw.
A7.
Given n=4, 2 = 12 rad/s cw.
Number of instantaneous centers,
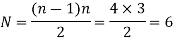
Make a list of all the instantaneous centers as follows:
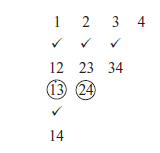
we have
Center 13: at the intersection of line joining 12, 23 and 14, 34.
Center 24: at the intersection of line joining 12, 14 and 23, 34.
5. By measurements, we have
13-23 = 550 cm
13-34 = 390 cm
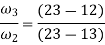
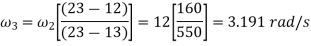
Now velocity of slider
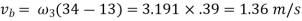
Q8. Define acceleration and its types. Illustrate the method of determining the acceleration of a link.
A8. Acceleration of a body can be defined as the rate of change of velocity with respect to time. Similar to velocity it can be of two types:
Acceleration of a link
let us assume a link OA of length r rotating in clockwise direction having angular velocity at the given instant and the angular acceleration in the direction of the angular velocity shown in figure (a).
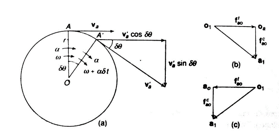
Components of angular acceleration of a rotating link.
In the figure (b) shows the acceleration diagram of the link OA when the acceleration supports the velocity while figure (c) shows the acceleration diagram when acceleration opposes the velocity.
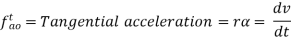

Total acceleration of the link OA is given by the vector sum of tangential and centripetal acceleration i.e.
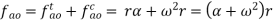
And the direction is given by
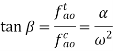
Q9. For the configuration of slider-crank mechanism shown in figure (a) with velocity diagram in figure (b). Calculate the:
(i) acceleration of the slider B.
(ii) acceleration of the point E
(iii) angular acceleration of link AB.
When OA rotates at 20 rad/s counter-clockwise.
Solution.
Given: a = 20 rad/s in ccw, OA= 480 mm, AB = 1600 mm, AE= 450mm
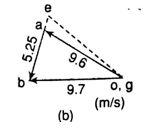
A9.
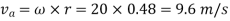
Note: Generally, in order to calculate the acceleration first we have to draw the velocity diagram. Here it is given in question itself in figure (b).
Now write the governing vector equation for acceleration.
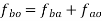
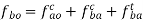
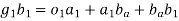
Now set the vector table for acceleration
S.No. | Vector | Magnitude (m/s2) | Direction | Sense |
1. |
|
|
| O |
2. |
|
|
| A |
3. |
| - |
| - |
4. |
| - |
| - |
The acceleration diagram is to be drawn as follows:
a) Select the pole point o1 and g1.
b) Draw vector  .
.
c) Add the vector 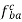 to vector
to vector 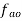 .
.
d) For the vector 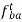 , draw a line perpendicular to AB through the head ba of the vector
, draw a line perpendicular to AB through the head ba of the vector  .
.
e) For the vector 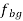 draw a line through g1 parallel to the line of motion of the slider.
draw a line through g1 parallel to the line of motion of the slider.
(i) Acceleration of slider at B, by measurement.
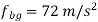
Direction of fb is same as of vb, hence slider is accelerating.
(ii) Now we can locate the point e1 on b1a1 by producing such that
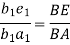
Hence,
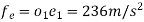
(iii) 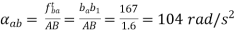
Q10. The given figure shows a slider moving outwards on a rod with a velocity of 4 m/s2. The rod has an angular velocity of 6 rad/s counter clockwise about O and an angular acceleration of 20 rad/s2 clockwise. Determine the absolute acceleration of slider.
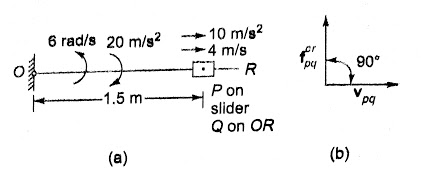

A10.
Writing acceleration equation

Now set the vector table
S.No. | Vector | Magnitude (m/s2) | Direction | Sense |
1. |
|
|
| ← |
2. |
|
|
| ↓ |
3. |
| 10 |
| - |
4. |
|
|
| - |
Figure (b) represents the method to obtain the Coriolis component. The velocity vector of the slider is rotated by 90° in the angular direction of the rod.
Draw the acceleration diagram shown in figure (c) as described below:
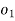
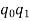
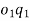
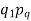
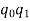
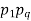
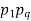
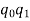
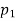
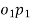
By measurement, we get 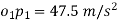 .
.