Unit 3
Metal Cutting
Q1. In a machining operation that approximates orthogonal cutting, the cutting tool has a rake angle = 100. The chip thickness before the cut to = 0.50 mm and the chip thickness after the cut tc = 1.125 in. Calculate the shear plane angle and the shear strain in the operation.
ANS: The chip thickness ratio can be determined as

The shear plane angle is given by
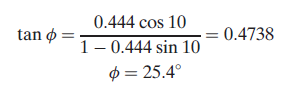
Finally, the shear strain is calculated as
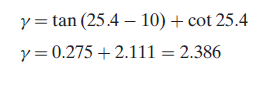
Q2. Suppose in above example cutting force and thrust force are measured during an orthogonal cutting operation: Fc = 1559 N and Ft = 1271 N. The width of the orthogonal cutting operation w = 3.0 mm. Based on these data, determine the shear strength of the work material.
ANS: From Example 1, rake angle a = 100, and shear plane angle f = 25.40. Shear force can be computed as
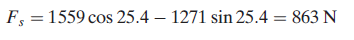
The shear plane area is given by

Thus the shear stress, which equals the shear strength of the work material, is
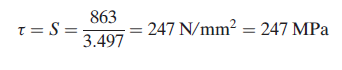
Q3. Using the data and results from our previous examples, determine (a) the friction angle and (b) the coefficient of friction.
ANS: (a) From Example 1, 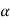 = 100, and
= 100, and 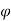 = 25.40. The friction angle can be estimated:
= 25.40. The friction angle can be estimated:

(b) The coefficient of friction is given by
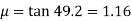
Q4. The cutting force and thrust force in an orthogonal cutting operation are 1470 N and 1589 N, respectively. The rake angle = 5°, the width of the cut = 5.0 mm, the chip thickness before the cut = 0.6, and the chip thickness ratio = 0.38. Determine (a) the shear strength of the work material and (b) the coefficient of friction in the operation.
ANS: (a) φ = tan-1(0.38 cos 5/(1 - 0.38 sin 5)) = tan-1(0.3916) = 21.38°
Fs = 1470 cos 21.38 – 1589 sin 21.38 = 789.3 N
As = (0.6)(5.0)/sin 21.38 = 3.0/.3646 = 8.23 mm2
S = 789.3/8.23 = 95.9 N/mm2 = 95.9 MPa
(b) φ = 45 + α/2 - β/2; rearranging,
β = 2(45) + α - 2φ β = 2(45) + α - 2(φ) = 90 + 5 – 2(21.38) = 52.24°
μ = tan 52.24 = 1.291
Q5. In an orthogonal cutting operation, the rake angle = -5°, chip thickness before the cut = 0.2 mm and width of cut = 4.0 mm. The chip ratio = 0.4. Determine (a) the chip thickness after the cut, (b) shear angle, (c) friction angle, (d) coefficient of friction, and (e) shear strain.
ANS:
(a) r = to/tc, tc = to/r = 0.2/.4 = 0.5 mm
(b) φ = tan-1(0.4 cos(–5)/(1 - 0.4 sin(–5))) = tan-1(0.3851) = 21.1°
(c) β = 2(45) + α - 2(φ) = 90 + (-5) - 2(21.8) = 42.9°
(d) μ = tan 42.9 = 0.93
(e) γ = cot 31.8 + tan(31.8 - 15) = 2.597 + 0.489 = 3.09
Q6. A carbon steel bar 7.64 inch in diameter has a tensile strength of 65,000 lb/in2 and a shear strength of 45,000 lb/in2. The diameter is reduced using a turning operation at a cutting speed of 400 ft/min. The feed is 0.011 in/rev and the depth of cut is 0.120 in. The rake angle on the tool in the direction of chip flow is 13°. The cutting conditions result in a chip ratio of 0.52. Using the orthogonal model as an approximation of turning, determine: (a) the shear plane angle, (b) shear force, (c) cutting force and feed force, and (d) coefficient of friction between the tool and chip.
ANS:
(a) φ = tan-1(0.52 cos 13/(1 - 0.52 sin 13)) = tan-1(0.5738) = 29.8°
(b) As = tow/sin φ = (0.011)(0.12)/sin 29.8 = 0.00265 in2.
Fs = AsS = 0.00587(40,000) = 119.4 lb
(c) β = 2(45) + α - 2(φ) = 90 + 10 - 2(29.8) = 43.3°
Fc = Fscos (β – α)/cos (φ + β – α)
Fc = 264.1 cos (43.3 - 13)/cos (29.8 + 43.3 - 13) = 207 lb
Ft = Fssin (β – α)/cos (φ + β – α)
Ft = 264.1 sin (43.3 - 13)/cos (29.8 + 43.3 - 13) = 121 lb
(d) μ = tan β = tan 43.3 = 0.942
Q7. Determine the values of C and n in the plot of graph, using two of the three points on the curve and solving simultaneous equations of the form of equation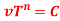 .
.

ANS:
Choosing the two extreme points: v =160m/min, T = 5min; and v = 100m/min,
T = 41 min; we have
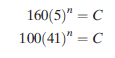
Setting the left-hand sides of each equation equal,
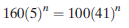
Taking the natural logarithms of each term,
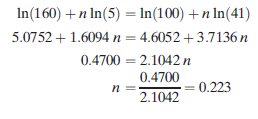
Substituting this value of n into either starting equation, we obtain the value of C:
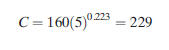
or
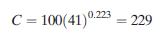
The Taylor tool life equation for the data of graph is therefore

Q8. A series of tool life tests are conducted on two work materials under identical cutting conditions, varying only speed in the test procedure. The first material, defined as the base material, yields a Taylor tool life equation vT0.28 = 350, and the other material (test material) yields a Taylor equation vT0.27 = 440, where speed is in m/min and tool life is in min. Determine the machinability rating of the test material using the cutting speed that provides a 60-min tool life as the basis of comparison. This speed is denoted by v60.
ANS: The base material has a machinability rating = 1.0. Its v60 value can be determined from the Taylor tool life equation as follows:
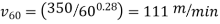
The cutting speed at a 60-min tool life for the test material is determined similarly:
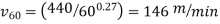
Accordingly, the machinability rating can be calculated as

Q9. Machinability ratings are to be determined for a new work material using the cutting speed for a specified tool life as the basis of comparison. For the base material (B1112 steel), test data resulted in Taylor equation parameter values of n = 0.24 and C = 450, where speed is m/min and tool life is min. For the new material, the parameter values were n = 0.28 and C = 490. Cemented carbide tools were used. Compute machinability ratings for the new material using as the tool life criterion (a) 60 min, (b) 10-min, and (c) 1.0 min. (d) What do the results show about the difficulties in machinability measurement?
ANS:
(a) Base material: v60 = 450/600.24 = 168.4 m/min
New material: v60 = 490/600.28 = 155.7 m/min
MR = 155.7/168.4 = 0.925 = 92.5%
(b) Base material: v10 = 450/100.24 = 259.0 m/min
New material: v10 = 490/100.28 = 257.2 m/min
MR = 257.2/259.0 = 0.993 = 93.3%
(c) Base material: v1 = 450/10.24 = 450 m/min
New material: v1 = 490/10.28 = 490 m/min
MR = 490/450 = 1.089 = 108.9%
(d) Different test conditions often result in different machinability results.
Q10. Machinability ratings are to be determined for a new steel. For the base material (B1112), test data resulted in Taylor equation parameters n = 0.28 and C = 500. For the new material, the Taylor parameters were n = 0.25 and C = 430. Cutting speed units are m/min, and tool life units are min. The tooling was cemented carbide. (a) Compute machinability ratings for the new material using the following criteria: (a) cutting speed for a 30-min tool life and (b) tool life for a cutting speed of 150 m/min.
ANS:
(a) Base material: v30 = 500/30.28 = 192.9 m/min
New material: v30 = 430/30.25 = 183.7 m/min
MR = 183.7/182.8 = 0.95 = 95%
(b) Base material: T150 = (500/150)1/.28 = (3.33)3.571= 73.7 min
New material: v10 = (430/150)1/.25 = (2.87)4.0 = 67.8 min
MR = 67.8/73.7 = 0.92 = 92%