undefined | unit 2 design of shaft

DME

Unit-2

Design of Shaft

Q1) What is shaft? Explain its category.

A1) Shaft is a rotating machine element which is used to transmit power from one place to another. In order to transfer the power from one shaft to another, the various member such as pulleys, gears etc.

It is the machine members, mostly cylindrical in cross-section, which support the revolving parts of a machine, such as pulleys, gear, flywheels etc.

Shafts are given different name on the basis of their application. Some of the specific categories of transmission shafts are as follows:

Axle: It is similar in shape to the shaft, which is a stationary machine element and is used for the transmission of bending moment only. It simply acts as a support from rotating body such as hoisting drum etc.

Spindle: It is a short shaft that imparts motion either to a cutting tool like drill machine etc.

Counter shaft: It is a secondary shaft, which is driven by the main shaft and from which the power is supplied to a machine component. It rotates counter to the direction of main shaft and used in multi stage gear box.

Q2) What are different stresses evolved in shaft?

A2) The following stresses are induced in the shafts:

Shear stresses due to the transmission of torque (due to torsional load).

Bending stresses (tensile or compressive) due to the forces acting upon the machine elements like gears and pulleys as well as the self weight of the shaft.

Stress due to combined torsional and bending loads.

Q3) Explain the design of the shaft for static load.

A3) The static load safety factor is calculated by dividing the basic static load rating (C0) by the static equivalent load of the most heavily loaded bearing.

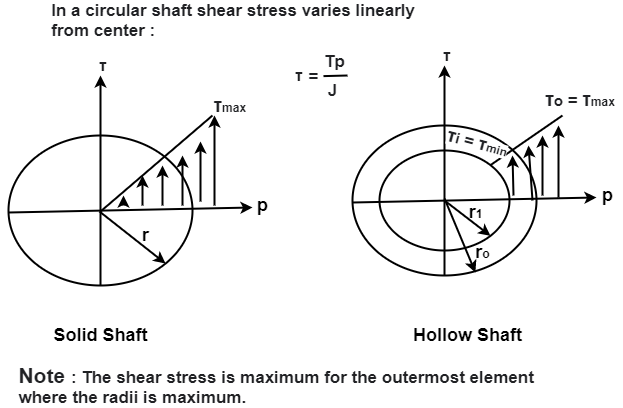
When the shaft is subjected to a twisting moment (or torque) only, then the diameter of the shaft only may be obtained by using the torsion equation. We know that T/J=Ϡ/r……………………………..(i)

Where, T= twisting moment acting on the shaft

J=Polar moment of inertia of the shaft

Ϡ= Torsional shear stress

r= distance from neutral axis to the outermost fibre

=d/2, where d is the diameter of shaft

Q4) Discuss the considered combined stress exerted on shaft while design.

A4) When the shaft is subjected to combination of torque and bending moment, principal stresses are calculated and then different theories of failure are used. Bending stress and torsional shear stress can be calculated using the above relations.

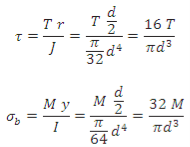
Maximum Shear Stress Theory

Maximum shear stress is given by,

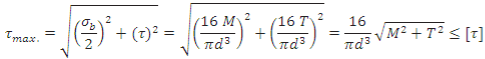
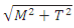is called equivalent torque, Te, such that

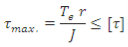
Maximum Principal Stress Theory

Maximum principal stress is given by,

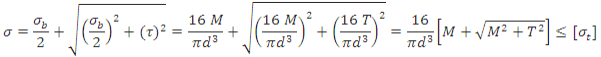
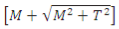is called equivalent bending moment, Me, such that

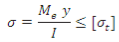
Question 5: Explain the design of the shaft based on deflection method.

Answer: A shaft is a part of a machine or system of machines, and is used to transmit power by virtue of its torsional strength, or resistance to twisting. Shafts are almost always made of metal and are usually circular in cross-section, being sometimes made hollow.

Shaft design based on the deflection:

Maximum bending stress developed in a shaft is given by,

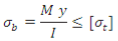
where M = Bending Moment acting upon the shaft,

I = Moment of inertia of cross-sectional area of the shaft about the axis of rotation

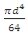= for solid shafts with diameter d

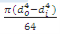= for hollow shafts with do and di as outer and inner diameter.

y = Distance from neutral axis to the outer most fibre = d / 2 (or do/2)

So dimensions of the shaft subjected to bending moment can be determined from above relation for a known value of allowable tensile stress.

Q6) Explain the design of shaft based on the strength.

A6) Transmission shafts are subjected to axial tensile force, bending moment or torsional moment or their combination.

Most of the transmission shafts are combined bending and torsional moment. The design of transmission shafts means finding diameter or inner or outer diameter in case of hollow shaft from the strength and rigidity consideration. Design of shaft subjected to pure axial load.

Let P be the axial load

d = required diameter of the shaft

σt=permissible tensile load

σt= P/A=(P)/(πd2/4)

or, σt=(4P)/(πd2)

or, d=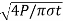

for hollow shaft

σt=(P)/(π(do2- di2/4)

Shaft subjected to pure bending moment

σb=Mby/I

σb=32Mb/πd3

For hollow shaft

I=(π(do4- di4)/64

Shaft subjected to pure torsional moment, the torsional shear stress is given by

Ϡ=Tr/J

For solid shaft

It is, 16T/πd3

In case of hollow shaft

J=(π(do4- di4)/32

Q7) A line shaft rotating at 300rpm is to transmit 20 kW. The shaft is having an allowable stress of 50 MPa. Determine the diameter of the shaft (neglecting the bending moment on the shaft)

A7) N=300 rpm, P=20 kW, Ϡ=50 MPa, d= diameter of shaft

We know that, P=2πNT/60

T=P×60/2πN

T= 636.61 N-m=636.61×10 N-mm

We know that, T=π/16×Ϡ×d3

d =40mm

Q8) What is critical speed of shaft?

A8) The critical speed is the theoretical angular velocity which excites the natural frequency of a rotating object, such as a shaft. As the speed of rotation approaches the objects natural frequency, the object begins to resonate which dramatically increases systemic vibration.

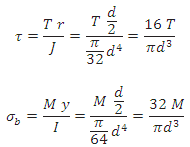
For a rotating shaft if the centripetal force is equal to the elastic restoring force, the deflection increases greatly and the shaft is said to "whirl”.

Q9) What are the factors affecting the critical speed of the shaft and also mention the factors affecting the critical speed?

A9) For a rotating shaft if the centripetal force is equal to the elastic restoring force, the deflection increases greatly and the shaft is said to "whirl”

Below and above this speed this effect is not pronounced

This critical (whirling speed) is dependent on: –

The shaft dimensions –

The shaft material and –

The shaft loads

The factor which affects the critical speed of a shaft is

Diameter of the disc,

Span of the shaft, and

Eccentricity.

For linear motion:

Power = F.v (force x velocity)

For rotational motion

Power P = Torque x angular velocity

= T (in-lb).w (rad/sec) in-lb/sec

= T.(2 p n/60) in-lb/sec [n=rpm]

= T.(2 p n/(60*12*550)) HP [HP=550 ft-lb/sec]

= T.n/63,025 HP

Or, T= 63,025HP/n (in-lb), where n = rpm

Similarly, T= 9,550,000kW/n (N-mm), where n = rpm

Q10) What is sliding contact and roller bearing?Explain the analysis of sliding contact bearing.

A10) Sliding contact bearing: In this bearing, the sliding action takes place along the surface of contact between the moving element and fixed element. The sliding contact bearing is known as plain bearing.

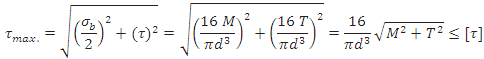
Rolling contact bearing: In this type of bearing, steel balls or rollers are interposed between the working surfaces. These bearings are also known as anti-friction bearings due to less friction imposed on moving element.

Length to diameter ratio:

Length to diameter ratio affects the performance of the bearing

A long bearing has more load carrying capacity but are more susceptible to metal to metal contact

A short bearing has greater side flow

L/D > 1 (long bearing)

L/D < 1 (short bearing)

L/D = 1 (square bearing)

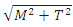
b. Unit bearing pressure:

It is load per unit of projected area of the bearing in running condition •

It depends on bearing materials, operating temperature, nature and frequency of load and service conditions.

The values of unit bearing pressure based on past experience are provided in the design data book.

c. Start up load:

It is static load when the shaft is stationary

Mainly consist of dead weight of shaft and its accessories

The unit bearing pressure for the starting conditions should not exceed 2 MPa

d. Radial clearance (c):

Should be small to provide the necessary velocity gradient

This requires:

Costly finishing operations

Rigid mounting of the bearing assembly

Clean lubricating oil without any foreign particle

Practical value of c is 0.001 r Material Radial clearance Babbits 0.001 r to 0.00167 r Copper lead 0.001 r to 0.01 r Aluminium alloys 0.002 r to 0.0025 r

e. Minimum oil film thickness (h0 ) :

The surface finish of the journal and the bearing is governed by the value of minimum oil film thickness selected by the designer and vice versa.

There is a lower limit for the minimum oil film thickness below which metal to metal contact occurs and hydrodynamic film breaks

The lower limit is given by h0 = 0.0002 r

f. Maximum oil film temperature:

The lubricating oil tends to oxidize when operating temperature exceeds 120°C

Also the surface of the bearing material tends to soften at 125°C

Therefore, operating temperature should be kept within limits

The limiting temperature is 90°C for bearings made of Babbit material

Sign Up