Unit - 1
Lateral Earth Pressure and Retaining Structure
Q1) What are the assumptions made by Rankine for Earth pressure?
A1)
Assumptions of the Rankine theory for active earth pressure are as follows:
- The soil mass is semi-infinite, homogeneous dry and cohesionless.
- The ground surface is plane which may be horizontal or inclined.
- The back of wall is vertical a smooth.
- The wall yields about the base thus satisfies deformation condition for plastic equilibrium.
- The soil element is in state of plastic equilibrium i.e., on verge of failure.
Q2) Explain Earth pressure at rest?
A2)
- It has been shown that active pressure exerted on the ranting wall resulting from slight movement of the wall away from the backfill is associated with the expansion of the soil and passive pressure exists when the movement of the retaining towards the backfill which tends to compress the soil horizontally. In short, passive pressure is associated with compression.
- When a soil element at a depth 'z' below the ground surface not subjected to any strain in the natural state, then the soil element in this condition is called as soil at rest condition. Earth pressure at rest exerted on the back of a rigid retaining wall can be determined by using the theory of elasticity in which soil is assumed to be elastic, homogeneous, isotropic and semi-infinite.
- At rest condition, the earth pressure is expressed as follows,
P0=K0 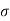 z
z
Where K0=Coefficient of earth pressure
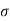 z=Effective vertical stress at depth a
z=Effective vertical stress at depth a
- Fig. Shows a retaining wall of height H at rest. It is possible to determine the lateral pressure by using theory of elasticity considering the soil mass to be homogenous, elastic isotropic and a semi-infinite material provided there is no displacements at all.

Fig.: earth pressure at rest
Q3) Explain Rankine’s Theory?
A3)
Rankine’s State of Plastic Equilibrium in soils:
- Plastic equilibrium of soil: When every point of the soil body is on the verge of failure, then a body of soil is said to be in plastic equilibrium. In another word; every point of soil mass at rest condition is brought on the verge of failure by applying tension or compression, then the state so occurred is termed as a general state of plastic equilibrium.
- Rankine's was the only engineer who developed the concepts of plastic equilibrium to solve the stability problems.
- When plastic equilibrium conditions are realized in limited zones of soil, then it is termed as the local state of plastic equilibrium. The development of earth pressure on the retaining wall is part of backfill comes under the plastic equilibrium condition.
- Rankine considered a semi-infinite mass of soil comes under a horizontal surface and a vertical boundary as shown in Fig.
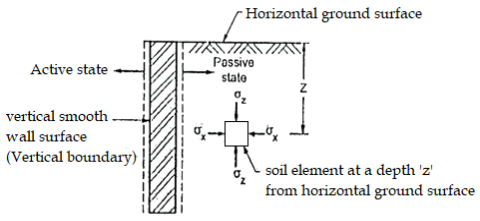
Fig.: A semi-infinite mass of soil bound by a horizontal surface and a vertical boundary
- Rankine assumed the soil mass to be homogenous, cohesionless and dry
- Consider a soil element at a depth 'e' subjected to horizontal stress and vertical stress. There are no shear stresses acting on the horizontal and vertical planes, hence
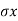 and
and 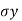 are the principal stresses.
are the principal stresses. - When the soil mass as a whole is stressed in such way that the principal stresses of every point are in the same direction then it set up the network of failure plane. This network of failure plane is called as slip line field as shown in fig. Slip line field is equally inclined to the principal planes. When sufficient deformation of mass take place, only then plastic equilibrium is set up.
Q4) Explain Active and Passive states due to wall movement?
A4)
When Wall Moves Away from Backfill:
- The value of horizontal stress decreases when away from backfill. If the expansion of soil element is more enough, then the value of horizontal stress (
 decreases to a minimum value and state of plastic equilibrium is set up called as active Rankine state as shown in Fig.
decreases to a minimum value and state of plastic equilibrium is set up called as active Rankine state as shown in Fig. - The Mohr's stress circle shows the state of elastic equilibrium as shown in Fig.
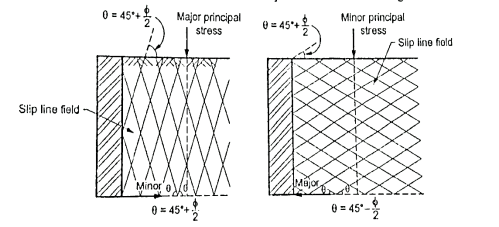
Fig.: Active and passive Rankine state due to wall movement
Active Rankine state
- When the Mohr's stress circle touches the strength line drawn for the soil, then soil mass is active Rankine state.
- Note that plastic equilibrium state is developed due to decrease in the value of horizontal stress (
 ) it means it should be minor principal stress (
) it means it should be minor principal stress (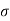 ); vertical stress (
); vertical stress (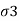 ) and major principal stress (
) and major principal stress (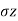 ), Minor principal stress due to decrease in the value of a, (horizontal stress) and Major principal stress.
), Minor principal stress due to decrease in the value of a, (horizontal stress) and Major principal stress.
When Wall Move towards the Backfill
- In such case, uniform compression is hold in the horizontal direction. There is an increase of horizontal stress (
 ) from its original value, but vertical stress (
) from its original value, but vertical stress (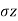 ) remains constant.
) remains constant. - The diameter of stress circle becomes smaller due to increase of deformation and then reduces to zero. When the horizontal stress becomes more than vertical stress i.e.,
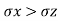 ,then diameter of stress circle increases until a state of plastic equilibrium is reached. At this state, horizontal stress (
,then diameter of stress circle increases until a state of plastic equilibrium is reached. At this state, horizontal stress (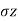 ) is maximum and hence it is a major principal stress (
) is maximum and hence it is a major principal stress ( ) but
) but 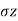 , (vertical stress) becomes minor principal stress
, (vertical stress) becomes minor principal stress 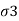 .
.
Passive Rankine state
- When Mohr's stress circle drawn with
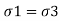 , an
, an d touches the strength envelope, then it will be reached with the maximum value of
d touches the strength envelope, then it will be reached with the maximum value of  This state of soil of reaching the maximum value of o, is called as passive Rankine state and pressure so developed is called as passive earth pressure (pp).
This state of soil of reaching the maximum value of o, is called as passive Rankine state and pressure so developed is called as passive earth pressure (pp).
Q5) Explain Earth pressure on retaining wall due to submerged backfill?
A5)
- Fig. Shows the retaining wall with backfill submerged by the natural water table saturated water. In such case, the lateral pressure is the sum of the two components.
These two components are as follows,
- Lateral pressure caused by submerged weight (
 ) of the soil, k, y, z and
) of the soil, k, y, z and - Lateral pressure caused by water (
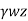 )
)

Fig: Submerged backfill
Here at any depth 2 below the horizontal surface-active pressure is given by the following expression,
Pa=Ka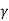 sz+
sz+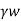 z
z
Where, Pa=active pressure
 s= submerged weight of soil (y)
s= submerged weight of soil (y)
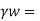 unit weight of water
unit weight of water
Fig. Shows the active earth pressure distribution diagram at any depth 'z' and at the depth H.
The active pressure at the base of wall, where z H is given by the following expression,
Pa=Ka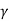 sH+
sH+ H
H
Q6) Explain backfill with uniform surcharge?
A6)
- Fig. Shows the retaining wall with horizontal backfill which is loaded by a uniformly distributed surcharge of intensity "q" by assuming the vertical pressure at any, depth is increased by "q".
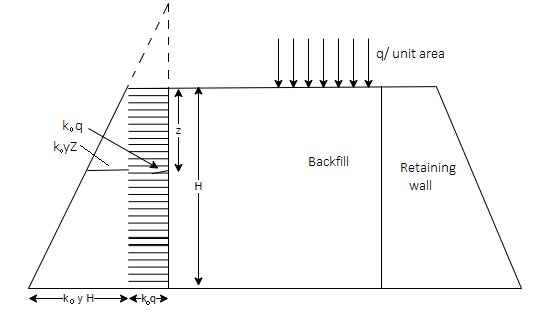
Fig.: Retaining wall with backfill carrying uniform surcharge
∴Lateral active pressure at any depth 'z' is given by the following expression
Pa=Ka z+Kaq ….(at any depth z)
z+Kaq ….(at any depth z)
Where z =H, then, active pressure at the base is given
Pa=Ka H+Kaq .....(at height H from base of wall)
H+Kaq .....(at height H from base of wall)
Q7) Explain Backfill with sloping surcharge?
A7)
- Rankine's theory can also be applied for backfill with sloping surface at the constant angle
 to the horizontal.
to the horizontal. - To determine the active earth pressure in such case by Rankine's theory, an additional assumption is considered that the vertical stress and lateral pressure are conjugate stresses.
- The active earth pressure at a depth 'z' acting parallel to the slope is given by the following expression:
Pa= Ka γz , ...For sloping surface
, ...For sloping surface
Where, Ka=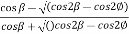
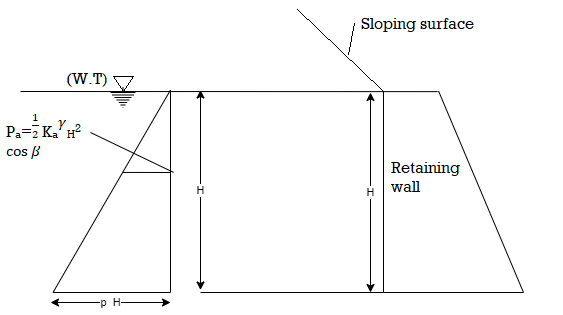
Fig.: backfill with sloping surface
For horizontal ground surface; 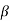 =0
=0
Ka=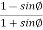
The total active pressure P, for a retaining wall having height 'II' is given by the following expression:
Pa= Ka
Ka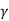 H2
H2 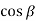
Q8) Explain Layered backfill?
A8)
There are two cases for lateral pressure in layered soils which are as follows
- Same angle of shearing resistance
- Different angle of shearing resistance i.e.,
(a) Lateral pressure for layered cohesionless soil
1. Same angle of shearing resistance with cohesionless soil layers
- In this case, if
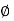 values for retained materials are considered to be same, then the pressure distribution diagram shows the same values of lateral pressure at same depth for same value of vertical stress (
values for retained materials are considered to be same, then the pressure distribution diagram shows the same values of lateral pressure at same depth for same value of vertical stress ( ) as shown in Fig.
) as shown in Fig.
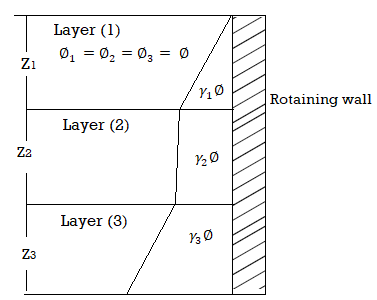
Fig: Layered soil with same angle of shearing resistance
(2) Different angle of sheering resistance with cohesionless soil layer
- When the upper and lower layers with different values of
 are considered, then the lateral pressure have a lower value for higher angle of friction and higher value of lateral pressure for a smaller angle of friction.
are considered, then the lateral pressure have a lower value for higher angle of friction and higher value of lateral pressure for a smaller angle of friction.
Fig. Shows layered soil with different angle of shearing resistance.
Let consider for the two layers as shown in Fig.
for the two layers as shown in Fig.
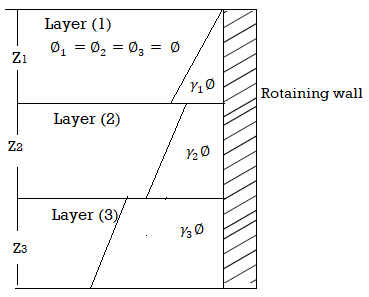
Fig.: Layered soil with different angle of shearing resistance
For these two layers, ka1 > ka2, the active pressure are as follows:

Q9) Explain Coulomb’s Wedge theory?
A9)
- Rankine's theory of earth pressure considers the theory of plasticity approach to find the stresses in the soil mass. The Rankine's theory is only applicable to smooth vertical wall. There are various ideal conditions used in practice of retaining wall problems.
- Coulomb's wedge theory can be applied to determine the active earth pressure for a backfill possessing both cohesion and effect of friction between the backfill and wall.
- Coulomb's theory considers a dry non-cohesive or dry cohesionless inclined backfill in which the lateral earth pressure required to balance the equilibrium of a sliding wedge with a slip surface can be determined.
Basic Assumptions of Coulomb's Wedge Theory:
Following are the various basic assumptions of coulomb's wedge theory
- The backfill is dry, non-cohesive (i.e., cohesionless), homogeneous, isotropic, soil (i.e., equal elastic properties in all direction). The backfill is elastically undeformable but breakable
- Backfill possessing both cohesion and internal friction or slip surface
- The failure surface or slip surface is a plane surface which passes through the heel of wall
- Failure is two dimensional. The backfill surface is plane and can be inclined.
- The position and the line of action of the earth pressure or direction of resultant earth pressure are known. The back of the wall can be inclined to the vertical
- The sliding wedge is itself considered as rigid body and the earth pressure is obtained by considering the limiting equilibrium of the sliding wedge as a whole.
Shape of the failure surface:
- The shape of the failure surface which makes one of the boundaries of the sliding wedge is actually curved near the bottom of the wall in both active and passive cases due to wall friction. Hence there is curvature in slip surface due to friction itself.
Active earth pressure (Pa) for C= 0 backfill:
- In case of cohesionless backfill (i.e., non-cohesive backfill, C= 0), there are three forces kept the wedge under equilibrium. These three forces are:
- Weight of wedge (W)
- Soil reaction force (R) on the failure plane and
- Earth pressure reaction (P)

Fig.: Wedge under the action of three forces, W, R and P
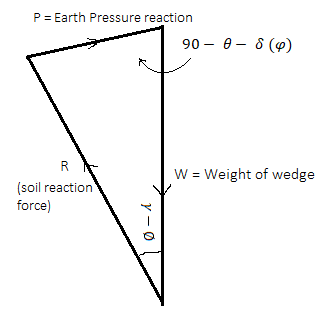
Fig.: Force triangle W, R and P
- Fig. Shows the force triangle drawn from the known value of W and direction of all the three forces and magnitude of P is determined for the assumed trial wedge.
- There is maximum wall reaction for critical step, plane and the wall should resist the maximum lateral pressure before it moves outward. Hence the maximum value of P is the active earth pressure.
- Note that in case of passive earth pressure, the wall should exert the smallest force so as to move the wedge for critical slip surface.
- In general; one of the drawbacks in coulomb's theory that it does not satisfy the static equilibrium condition. When the sliding surface is assumed to be plane, then three forces i.e., weight of wedge (W), soil reaction (R) and the earth pressure (P) acting on the sliding wedge do not meet at a common point. However, based on the other assumption, the coulomb’s theory is most effective in practice.
Active earth pressure for C-  backfill:
backfill:
- Coulomb's theory can be used to find out the active earth pressure (P) for a backfill possessing both cohesion and friction.
- Following are the various forces acting on the wedge of soil at failure for C- backfill
- Weight of soil wedge (W)
- Earth pressure reaction (P) acting at an angle below the normal
- Soil reaction (R) on the failure plane acting an angle below the normal
- Force of adhesion (C2) between soil and wall
- Cohesive force (C) on the failure plane
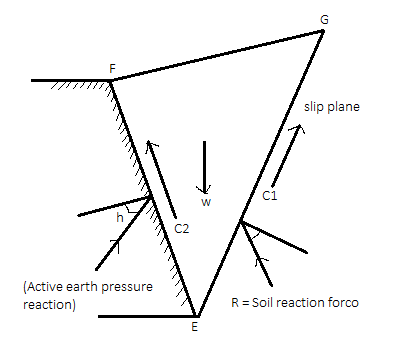
Fig.: Forces acting on soil wedges at failure
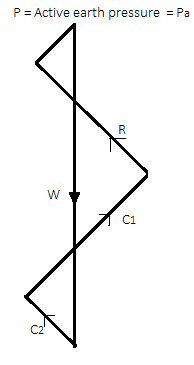
Fig.: Polygon of forces
The force polygon as shown in Fig. Is drawn from the known values of W. C, C, and direction of all five forces and the value of p i.e., active earth pressure can be determined by closing side of a polygon.
Here C1=Cu x length of the slip plane EG
C2= unit adhesion (Cw) x length of wall in contact with the soil EF
Q10) Explain Rebhan’s graphical solution?
A10)
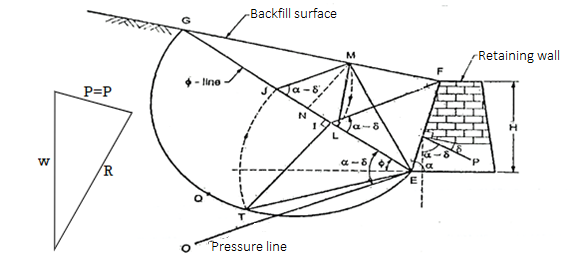
Fig.
Graphical method by poncelet construction based on Rebhan’s principles
- In 1871, Rebhan's represented a graphical method to determine the total active pressure (Pa) based on Coulomb's theory on a rough wall with a cohesionless, homogenous and inclined backfill as shown in Fig.
- Fig. Shows poncelet construction for non-cohesive soils or cohesionless soils (C = 0) based on the principles made by Rebhan.
Procedure of graphical method:
Following is the procedure of construction to find out the active earth pressure by graphical method refer Fig.
- Draw a retaining wall to a suitable scale and measure the backfill surface angle for required position as shown in Fig.
- Draw a -line EG such that it intersects the backfill surface at G.
- Draw a semi-circle BQG by taking diameter as EG.
- Draw the pressure line 'EO' at an angle of (a-5) with respect to o-line.
- Draw FI parallel to pressure line 'EO'.
- Draw a perpendicular to EG at I such that it cut the semi-circle at T.
- With centre E and radius ET, draw an are such that it cut EG at J.
- Draw JM parallel to FI
- Now EM is a rupture line
- Taking as a centre and IM as the radius draw at a such thar EG at L
After this construction from step 1 to 10, it shows the 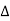 LIM. Area of
LIM. Area of 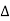 LIM in its natural unirs multiplied by the unit weight of the soil (
LIM in its natural unirs multiplied by the unit weight of the soil (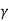 ) gives the active earth pressure (Pa) as follows:
) gives the active earth pressure (Pa) as follows:
Pa=Area of triangle LJM=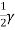 *JM*MN
*JM*MN
Where, 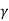 =unit wt of the soil
=unit wt of the soil
JM length of a triangle LJM
MN=height of 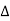 LJM
LJM
Pa=Active earth pressure
Q11) Explain Culmann’s graphical solution?
A11)
- Culmann's graphical method is rather general method than Rebhan's method. This method is same as the trial wedge method. The force triangle or force polygon can directly be constructed on o-line EG considering EG as a load line.
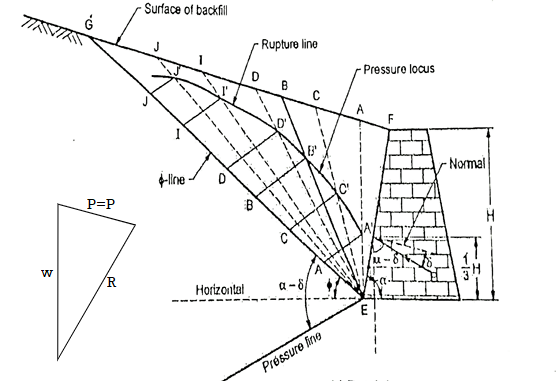
Fig.: Culmann’s graphical method for determining active earth pressure
- This method can be used to evaluate the coulomb's earth pressure fr ground sa face of any configuration, different types of surcharges and layered backfills.
- Fig. Shows the Culmann's graphical method of determine active earth pressure (P) for non-cohesive soils or cohesionless soils (i.e., C= 0)
Graphical construction procedure;
- Various steps involved in the procedure are as follows:
- EF it a retaining wall as shown in Fig. 5 in 1(a) drawn to a suitable scale.
- Draw -line EG at an angle with respect to horizontal.
- Mark on EG, the distances EA, EC, ED, EL, EJ etc. to a suitable scale representing the weight of wedges EFA, EFC, EFD, EFI, EFI etc. respectively.
- Draw lines parallel to pressure line ET from the points A, C, D, I J such that it intersects assumed rupture line EA, EC, ED, EI, EJ at points A, C, D,1, J respectively.
- Then point A', C, D, I', J' are joined by a smooth curve representing the pressure locus.
- Select point B' on the pressure locus in such way that the tangent to the curve at this point parallel to line EG
- Draw B'B parallel to the pressure line ET. The magnitude of B'B" itself in its natural units gives the active earth pressure (Pa)
- Points E and B' are joined and extended further so as to meet the surface of backfill at B Then EB is the rupture line.
- Note that, for the plane backfill surface, the point of application of active earth pressure (Pa) is at a height 1/3 of from the base of retaining wall.
Q12) Compute the active earth pressure at a depth of 4.5m in a sand whose angle of friction is 37 degree and density of 15.60KN/m3 in dry state.
A12)
Given: H = 4.5m,  = 37%,
= 37%,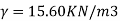
To compute the active earth pressure at a depth H in dry state
We know,
From Rankine's theory, active earth pressure (p) at a depth His given by:
Pa=Ka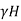 …. (1)
…. (1)
Where Ka=coefficient of active earth pressure=
∴Ka=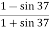 =0.248
=0.248
Substituting Ka=0.248 in equation 1 we get,
Pa=0.248×15.60×4.5
∴Pa=17.4kN/m3
Q13) A smooth vertical wall retains a level surface with  to a depth of 8m. Compute the total active pressure in dry condition and when water table rises to the GL Assume
to a depth of 8m. Compute the total active pressure in dry condition and when water table rises to the GL Assume
A13)
Given: H=depth=8m

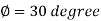

To compute the total active pressure Pa in dry condition:
Ka=Coefficient of active earth pressure=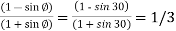
∴Total active earth pressure in dry condition (Pa)
=Ka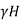 =1/3×18×8
=1/3×18×8
Pa=48KN/m3
To compute the total active earth pressure when water table rises to the GL (i.e., submerged soil)
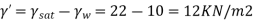
∴Total active earth pressure (Pa)
=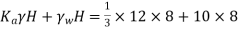
∴Pa=112KN/m2