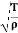Unit 1

OSCILLATION & WAVES

Q1) Derive differential equation for mechanical simple harmonic oscillators?

A10) The figure-1 depicts simple mechanical oscillator having mass attached to the spring. This structure is similar to Pendulum. It is also known as harmonic oscillator.

Figure: 1

If a body attached to a spring is displaced from its equilibrium position, the spring exerts a restoring force on it, which tends to restore the object to the equilibrium position. This force causes oscillation of the system, or periodic motion.
When the restoring force is directly proportional to the displacement from equilibrium, the resulting motion is known as simple harmonic motion and the oscillator is known as Harmonic Oscillator.

In this type of system body itself changes its position.

For mechanical oscillation two things are especially responsible i.e. Inertia & Restoring force.

Differential Equation

A particle is said to be execute simple harmonic oscillation is the restoring force is directed towards the equilibrium position and its magnitude is directly proportional to the magnitude and displacement from the equilibrium position.If F is the restoring force on the oscillator when its displacement from theequilibrium position is x, then

 F–x

Here, the negative sign implies that the direction of restoring force is opposite to that of displacement of body i.e. towards equilibrium position.

F= -kx          ............. (1)

Where, k= proportionality constant called force constant.

An example of such a simple system is the mass m, attached to a spring of stiffness k.

Figure: 2
 

In the case of a mass on a spring, the restoring force for small oscillations obeys Hooke’s law:

F=−kx,

where k is the stiffness of the spring. Here the coordinate x=0 corresponds to the point of equilibrium, in which the force of gravity is balanced by the initial tension of the spring.

Then, according to Newton’s second law, the movement of the mass will be described by the differential equation

mx′′=−kx,

⇒x′′+x=0.

Solution of differential equation is

x= Acosωt        

or

x = Acos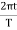

Thus, the mass on the spring will perform undamped harmonic oscillations with the circular frequency

ω=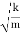

The time period of oscillation, respectively, will be equal to

T= =2π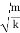

Phase

The form of Equations (4) implies that over each period of oscillation, as the time t increases its value bythe fixed amount T,the oscillator passes through a complete cycle of x values. Now, during such a cycle, thequantity 2πt/T (i.e. the argument of the sine and cosine functions) increases by 2π, and each additional incrementof 2π corresponds to another complete oscillation.

In this way the argument of the sine or cosine functionbehaves rather like an angle measured in radians, since that too would complete an additional cycle for eachincrease of 2π radians (or 360°). Of course, there’s not really any angle involved here since the motion is linearand the quantity 2πt/T has no units; what the argument of the periodic sine or cosine function tells us is the stagethat the moving particle has reached within its own cycle of oscillation. Nonetheless, the argument of theperiodic function is often referred to as the phase angle or simply the phase of the motion and is as likely to beexpressed in radians (or the corresponding number of degrees) as it is to be given as a unit less number.

A phase of 0 corresponds to the start of a cycle, a phase of 2π to the start of the next cycle, 4π the next, and soon. If the motion is halfway through the first cycle the phase is π.

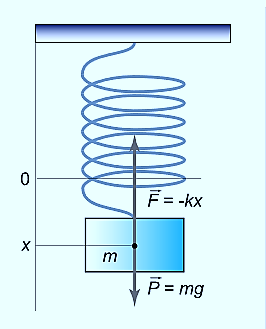
Figure: 3

Displacement as a function of time in SHM is given by

x(t)=Acos(2πt/T+φ)=Acos(ωt+φ)

whereφ is the phase or phase angle.

The Velocity is given by

v(t)=−Aωsin(ωt+φ)=−vmaxsin(ωt+φ),wherevmax=Aω=A

The Acceleration is a(t)=−Aω2cos(ωt+φ)=−amaxcos(ωt+φ), where amax=Aω2=A

A similar analysis of other oscillatory system which execute Simple harmonic motion.a simple pendulum – leads to the following formula for the oscillation period:

T=2π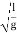

where L is the length of the pendulum, g is the acceleration of gravity.

In the case of a compound or physical pendulum, the period of oscillation is given by

T=2π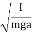

where I is the moment of inertia of the pendulum about the pivot point, m is the mass of the pendulum, a is the distance between the pivot point and the center of mass of the pendulum.

Example: oscillation of mass spring system, oscillation of fluid-column in a U-tube, oscillation of simple pendulum, rotation of eartharound the sun, oscillation of body dropped in a tunnel along earth diameter, oscillation of floating cylinder, oscillation of a circular ring suspended on a nail, oscillation of atoms and ions of solids, vibration of swings etc.

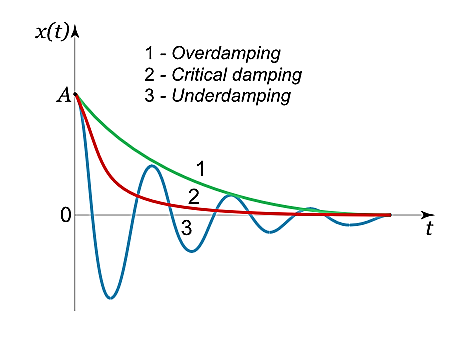
Q2) Discuss heavy, critical and light damping?

A2) In real systems, there is always a resistance or friction, which leads to a gradual damping of the oscillations. In many cases, the resistance force (denoted by FC) is proportional to the velocity of the body, that is

FC=−cx′.

Then, taking into account the force of resistance, the differential equation for the “mass-spring” system is written as

mx′′+cx′+kx=0,⇒x′′+ x′+x=0

We introduce the following notations: =2β, =. Here ω0 is the natural frequency of the undamped oscillator (previously, we denoted it as ω), β is the damping coefficient. In the new notations, the differential equation looks like

x′′+2βx′+x=0.

We will seek the solution of this equation as a function

x(t)=Aeλt.

The derivatives are given by

x′(t)=Aλeλt, x′′(t)=Aλ2eλt.

Substituting this into the differential equation, we obtain the algebraic characteristic equation:

Aλ2eλt+2βAλeλt+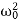Aeλt=0,

⇒λ2+2βλ+=0.

The roots of this equation are

D=4β2−4,

It can be seen that depending on the sign of the radicand β2−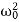, there may be three different types of solutions.

Case 1.Overdamping or Heavy Damping: β>ω0

When resistance to motion is. very strong, the system is said to be heavily damped. Can you name a heavily damped system of practical interest? Springs joining wagons of a train constitute the most important heavily damped system. In your physics laboratory, vibrations of a pendulum in a viscous medium such as thick oil and motion of the coil of a dead beat galvanometer are heavily damped systems.

In this case (the case of strong damping), the radicand is positive: β2>. The roots of the characteristic equation are real and negative. The general solution of the differential equation has the form

x(t)=C1eλ1t+C2eλ2t,

where the coefficients C1,C2, as usual, depend on the initial conditions.

It follows from this expression that there are no oscillations and the system returns to equilibrium exponentially, i.e. periodically(Figure 9).

Figure 9

Case 2. Critical Damping: β=ω0

You may have observed that on hitting an isolated road bump, a car bounces up and down and the occupants feel uncomfortable. To minimise this discomfort, the bouncing caused by the road bumps must be damped very rapidly and the automobile is restored to equilibrium quickly. For this we use critically damped shock absorbers. Critical damping is also useful in recording instruments such as a galvanometer (pointer type as well as suspended coil type) which experience sudden impulses. We require the pointer to move to the correct position in minimum time and stay there without executing oscillations. Similarly, a ballistic galvanometer coil is required to return to zero displacement immediately.

In the limiting case when β=ω0, the roots of the characteristic equation are real and coincide:

λ1=λ2=−β=−ω0.

Here the solution is given by the formula

x(t)=(C1t+C2)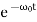

In this mode, the value of x(t) may even increase at the beginning of the process because of the linear factor C1t+C2. But in the end the deflection x(t) decreases rapidly due to the exponential decay with a characteristic time τ=2π/ω0.

Note that in this critical mode the relaxation occurs faster than in the case of the aperiodic damping (Case 1). Indeed, in this mode the relaxation time will be determined by the smaller (in absolute value) root λ1, and will be given by the formula

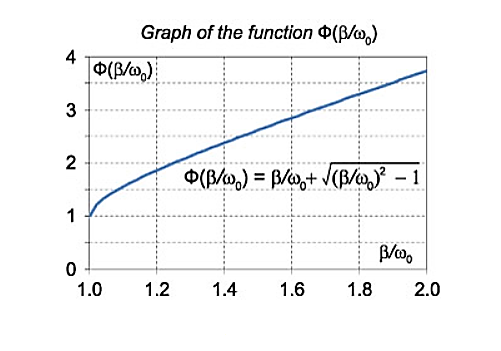
The function Φ(β/ω0) included in this expression is monotonically increasing. It is always greater than or equal to 1, as shown in Figure 10

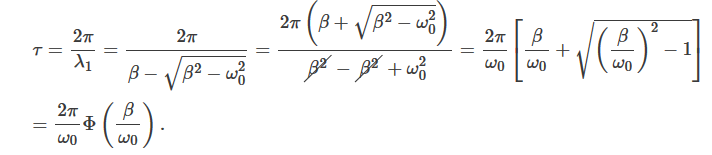
Figure 10

In the critical case (Case 2) the ratio βω0 is 1, and βω0>1 in the case of the aperiodic damping (Case 1). Therefore for the aperiodic damping mode, we can write

τ=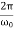Φ()>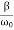

Thus, the critical damping mode provides the fastest possible return of the system to equilibrium. This is often used, for example, in door closing mechanisms.

Case 3. Under damping B  or Light Dampingβ<ω0

Here the roots of the characteristic equation are complex conjugate:

λ1,2=−β±i√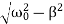

The general solution of the differential equation is oscillatory in nature and can be written as

x(t)=e−βt[C1cos(ω1t)+C2sin(ω1t)]

where the oscillation frequency ω1 is equal to

ω1=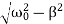

The resulting formula can be written in a somewhat different form:

x(t)=Ae−βtcos(ω1t+φ0),

whereφ0 is the initial phase of the oscillations and Acosφ0 is the initial amplitude of the oscillations. We see that classical damped oscillations occur in this mode. Here the oscillation frequency ω1 is less than the harmonic frequency ω0, and the oscillation amplitude decreases exponentially with e−βt.

Q3) What do you meant by Resonance?

A3) Resonance occurs when:-

Frequency of the external periodic force = Natural frequency of the system.

Definition:-The phenomena of producing oscillatory motion in a system by the influence of an external periodic force having the same frequency as that of natural frequency of the system is called Resonance.

Example:- Resonance causes disaster during earthquake. When the natural frequency of the building becomes equal to the frequency of the periodic vibration present in the earth during earthquake, then the building starts vibrating with large amplitude and hence it collapses.

Sit in front of a piano sometime and sing a loud brief note at it with the dampers off its strings. It will sing the same note back at you—the strings, having the same frequencies as your voice, are resonating in response to the forces from the sound waves that you sent to them. Your voice and a piano’s strings is a good example of the fact that objects—in this case, piano strings—can be forced to oscillate but oscillate best at their natural frequency. In this section, we shall briefly explore applying a periodic driving force acting on a simple harmonic oscillator. The driving force puts energy into the system at a certain frequency, not necessarily the same as the natural frequency of the system. The natural frequency is the frequency at which a system would oscillate if there were no driving and no damping force.

Most of us have played with toys involving an object supported on an elastic band, something like the paddle ball suspended from a finger in Figure 8. Imagine the finger in the figure is your finger. At first you hold your finger steady, and the ball bounces up and down with a small amount of damping. If you move your finger up and down slowly, the ball will follow along without bouncing much on its own. As you increase the frequency at which you move your finger up and down, the ball will respond by oscillating with increasing amplitude. When you drive the ball at its natural frequency, the ball’s oscillations increase in amplitude with each oscillation for as long as you drive it.

The phenomenon of driving a system with a frequency equal to its natural frequency is called resonance. A system being driven at its natural frequency is said to resonate. As the driving frequency gets progressively higher than the resonant or natural frequency, the amplitude of the oscillations becomes smaller, until the oscillations nearly disappear and your finger simply moves up and down with little effect on the ball.

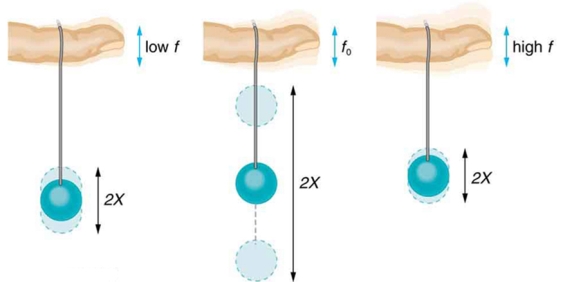
Figure  8:  The paddle ball on its rubber band moves in response to the finger supporting it. If the finger moves with the natural frequency f0 of the ball on the rubber band, then a resonance is achieved, and the amplitude of the ball’s oscillations increases dramatically. At higher and lower driving frequencies, energy is transferred to the ball less efficiently, and it responds with lower-amplitude oscillations.

Figure 9 shows a graph of the amplitude of a damped harmonic oscillator as a function of the frequency of the periodic force driving it. There are three curves on the graph, each representing a different amount of damping. All three curves peak at the point where the frequency of the driving force equals the natural frequency of the harmonic oscillator. The highest peak, or greatest response, is for the least amount of damping, because less energy is removed by the damping force.

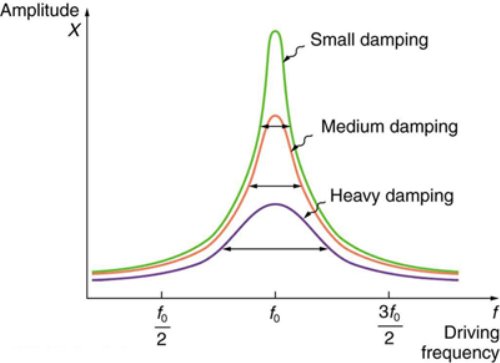
Figure 9:  Amplitude of a harmonic oscillator as a function of the frequency of the driving force. The curves represent the same oscillator with the same natural frequency but with different amounts of damping. Resonance occurs when the driving frequency equals the natural frequency, and the greatest response is for the least amount of damping. The narrowest response is also for the least damping.

It is interesting that the widths of the resonance curves shown in Figure 9 depend on damping: the less the damping, the narrower the resonance. The message is that if you want a driven oscillator to resonate at a very specific frequency, you need as little damping as possible. Little damping is the case for piano strings and many other musical instruments. Conversely, if you want small-amplitude oscillations, such as in a car’s suspension system, then you want heavy damping. Heavy damping reduces the amplitude, but the tradeoff is that the system responds at more frequencies.

Q4) Discuss in detail steady state motion of forced damped harmonic oscillator?

A4) Forced Oscillation

The oscillation of a oscillator is said to be forced oscillator or driven oscillation if the oscillator is subjected to external periodic force.

If an external periodic sinusoidal force Fcosωt  acts on a damped oscillator, its equation of motion is written as,

…………(1)

Where β= b/2m, 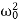= k/m and f0 = F/m , and β and 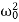respectively called as damping coefficient, natural frequency.

Equation (1) is also represented as

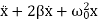= f0cosωt

Equation (1) represents the general equation of forced oscillation.

Equation (1) is a non-homogenous differential equation with constant co-efficient. For weak damping (>β 2) , the general equation contains,

x(t) = xc(t) + xp(t)

Where xc(t) is called complementary solution and its value is

  …………(2)

Now xp(t) is called the particular integral part.

Let us choose

xp(t) = P cos (ωt-δ)

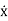(t)= -Pωsin(ωt-δ)

(t)=-Pω2cos(ωt-δ)        ……………(3)

Putting xp(t) , (t),(t)in equation (1) we get

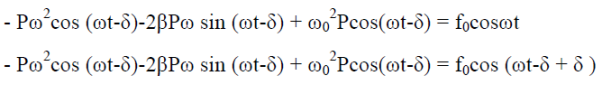
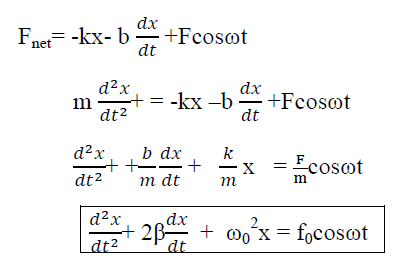
Now, comparing the coefficient of cos(ωt-δ) and sin (ωt-δ) on both sides,

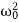(-ω2)P = f0cosδ        ……………(4)

2βPω = f0sinδ        ……………(5)

Squaring and adding eqn (4) & (5)

     ……….(6)

Now dividing equation (5) by (6)

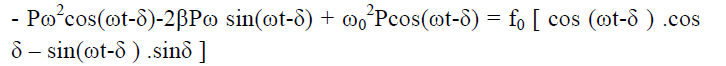
This is steady state solution. Now

x(t) = xc(t) + xp(t)

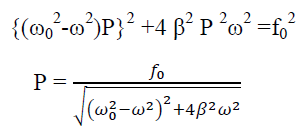
Steady state behaviour:

Frequency:-The Oscillator oscillates with the same frequency as that of the periodic force.

ω0and ω are very close to each other then beats will be produced and these beats are transient as it lasts as long as the steady state lasts. The duration between transient beats is determined by the damping coefficient β.

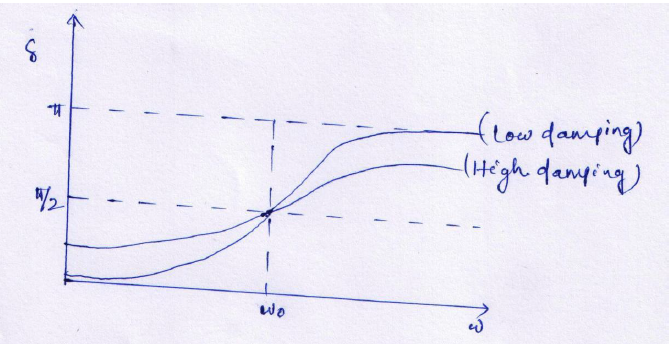
Phase: The phase difference δ between the oscillator and the driving force or between the displacement and driving is

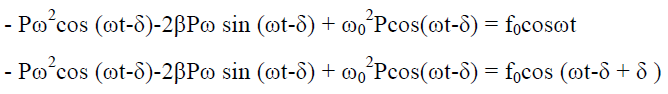
This shows that there is a delay between the action of the driving force and response of the oscillator.

Figure: 16

(In the above figure fQ= ω0 and fp= ω)

At ω=ω0, φ =π/2, the displacement of the oscillator lags behind the driving force byπ/2.

At ω<<ω0 then δ=0→δ=0

For ω>>ω0 then δ =-2p/ω→ -0=π

Amplitude: The amplitude of driven oscillator, in the steady state , is given by

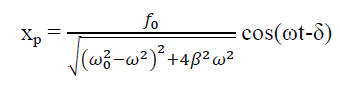
It depends upon (-ω2). If it is very small, then the amplitude of forced oscillation increases.

Case-1:At very high driving force i.eω>>ω0 and damping is small (β is small) or (β→0)

A =

A = =

Amplitude is inversely proportional to the mass of the oscillator & hence the motion is mass controlled motion.

Case-2:At very low driving force (ω<<ω0) and damping is small (β→0),

i.e. -ω2 =

A =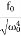

A = =

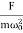
So, when the low driving force is applied to oscillator, the amplitude remains almost constant for low damping. The amplitude of the forced oscillator in the region ω<<ω0and β<ω0 is inversely proportional to the stiffness constant (k) and hence motion is called the stiffness controlled motion.

Case:-3 (Resistance controlled motion)

When angular frequency of driving force=natural frequency of oscillator i.e.(ω=ω0)

A = =

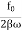
A=f/bω=f/bω0

Q5) Which of the following represent simple harmonic motion?

(i) x = A sin ωt + B cos ωt

(ii) x = A sin ωt+ B cos 2ωt

(iii) x = A eiωt

(iv) x = A ln ωt

A5)

(i) x = A sin ωt + B cos ωt

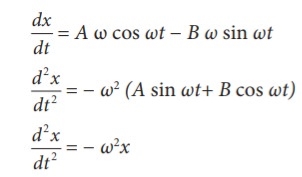
This differential equation is similar to the differential equation of SHM Therefore, x = A sin ωt + B cos ωt represents SHM.

(ii) x =A sin ωt + B cos2ωt

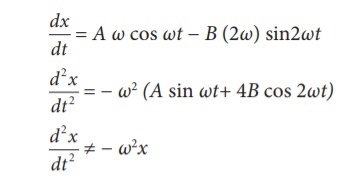
This differential equation is not like the differential equation of a SHM Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.

 (iii) x=Aeiωt

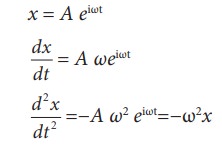
This differential equation is like the differential equation of SHM. Therefore, x = Aeiωt represents SHM.

(iv) x = A ln ωt

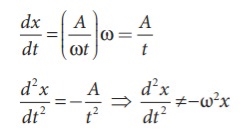
This differential equation is not like the differential equation of a SHM Therefore, x = A lnωt does not represent SHM.

Q6) Calculate the amplitude, angular frequency, frequency, time period and initial phase for the simple harmonic oscillation given below

a. y = 0.3 sin (40πt + 1.1)

b. y = 2 cos (πt)

c. y = 3 sin (2πt − 1.5)

A6) Simple harmonic oscillation equation is y = A sin(ωt + φ0) or y =A cos(ωt + φ0)

Q7) Show that for a simple harmonic motion, the phase difference between

a. displacement and velocity is π/2 radian or 90°.

b. velocity and acceleration is π/2 radian or 90°.

c. displacement and acceleration is π radian or 180°.

A7)

a.   The displacement of the particle executing simple harmonic motion

y = A sinωt

Velocity of the particle is

v = Aωcosωt = Aωsin(ωt+ π /2)

The phase difference between displacement and velocity is π/2.

b. The velocity of the particle is

v = A ωcosωt

Acceleration of the particle is

a = Aω2sinωt = Aω2cos(ωt+ π /2)

The phase difference between velocity and acceleration is π/2.

c. The displacement of the particle is y = A sinωt

Acceleration of the particle is

a = − A ω2 sin ωt = A ω2 sin(ωt + π)

The phase difference between displacement and acceleration is π.

Q8) A 500 μH inductor, 80/π2 pF capacitor and a 628 Ω resistor are connected to form a series RLC circuit. Calculate the resonant frequency and Q-factor of this circuit at resonance.

A8) L=500×10-6H; C = 80/π2 ×10−12 F; R = 628Ω

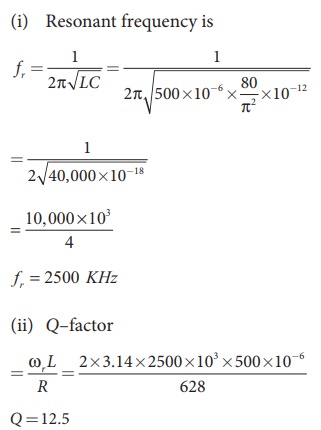
Q9) What do you meant by damped oscillations ?

A9) We have seen that the total energy of a harmonic oscillator remains constant. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). Simple harmonic motions which persist indefinitely without loss of amplitude are called free or undamped.

However, observation of the free oscillations of a real physical system reveals that the energy of the oscillator gradually decreases with time and the oscillator eventually comes to rest. For example, the amplitude of a pendulum oscillating in the air decreases with time and it ultimately stops. The vibrations of a tuning fork die away with the passage of time. This happens because, in actual physical systems, friction (or damping) is always present. Friction resists motion.

The presence of resistance to motion implies that frictional or damping force acts on the system. The damping force acts in opposition to the motion, doing negative work on the system, leading to a dissipation of energy. When a body moves through a medium such as air, water, etc. its energy is dissipated due to friction and appears as heat either in the body itself or in the surrounding medium or both.

There is another mechanism by which an oscillator loses energy. The energy of an oscillator may decrease not only due to friction in the system but also due to radiation. The oscillating body imparts periodic motion to the particles of the medium in which it oscillates, thus producing waves. For example, a tuning fork produces sound waves in the medium which results in a decrease in its energy.

All sounding bodies are subject to dissipative forces, or otherwise, there would be no loss of energy by the body and consequently, no emission of sound energy could occur. Thus, sound waves are produced by radiation from mechanical oscillatory systems. The electromagnetic waves are produced by radiations from oscillating electric and magnetic fields.

The effect of radiation by an oscillating system and of the friction present in the system is that the amplitude of oscillations gradually diminishes with time. The reduction in amplitude (or energy) of an oscillator is called damping and the oscillation are said to be damped.

When the energy of a oscillating system is gradually dissipated by friction and other resistances, the oscillations are said to be damped. Theoscillations gradually reduce or change in frequency or intensity or cease and the system rests in its equilibrium position.

Damped oscillations refer to oscillations where the oscillating object loses its energy to the surroundings.

Damping, in physics, restraining of vibratory motion, such as mechanical oscillations, noise, and alternating electric currents, by dissipation of energy. Unless a child keeps pumping a swing, its motion dies down because of damping. Shock absorbers in automobiles and carpet pads are examples of damping devices.

A system may be so damped that it cannot oscillate. Critical damping just prevents oscillation or is just sufficient to allow the object to return to its rest position in the shortest period of time.

Figure: 3

There are many types of mechanical damping. Friction, also called in this context dry, or Coulomb, damping, arises chiefly from the electrostatic forces of attraction between the sliding surfaces and converts mechanical energy of motion, or kinetic energy, into heat.The motion of aoscillating body is also checked by its friction with the gas or liquid through which it moves.

Q10) Define wave distinguish longitudinal and transverse wave?

A10) In physics a wave can be thought of as a disturbance or oscillation that travels through space-time accompanied by a transfer of energy. Wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium —that is with little or no associated mass transport.

The emphasis of the last point highlights an important misconception of waves. Waves transfer energy not mass.

A wave is a vibratory disturbance in a medium which carries energy from one point to another point without any actual movement of the medium.

There are two types of waves:

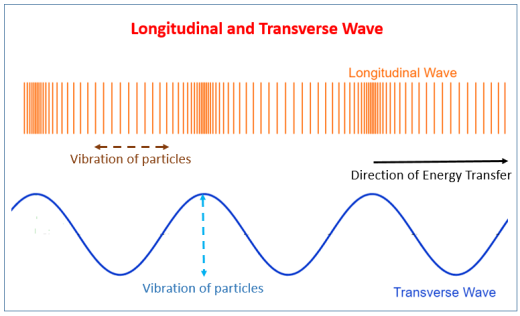
Longitudinal Waves: A wave in which the particles of the medium vibrate back and forth in the ‘same direction’ in which the wave is moving.  Medium can be solid, liquid or gases. Therefore, sound waves are longitudinal waves.These waves travel in the form of compressions and rarefactions.

Longitudinal waves have the same direction of vibration as their direction of travel. This means that the movement of the medium is in the same direction as the motion of the wave. Some longitudinal waves are also called compressional waves or compression waves. An easy experiment for observing longitudinal waves involves taking a Slinky and holding both ends. After compressing and releasing one end of the Slinky (while still holding onto the end), a pulse of more concentrated coils will travel to the end of the Slinky.In the example of the Slinky, each coil will oscillate at a point but will not travel the length of the Slinky. It is important to remember that energy, in this case in the form of a pulse, is being transmitted and not the displaced mass.

Longitudinal waves can sometimes also be conceptualized as pressure waves. The most common pressure wave is the sound wave. Sound waves are created by the compression of a medium usually air. Longitudinal sound waves are waves of alternating pressure deviations from the equilibrium pressure, causing local regions of compression and rarefaction. Matter in the medium is periodically displaced by a sound wave, and thus oscillates. When people make a sound, whether it is through speaking or hitting something, they are compressing the air particles to some significant amount. By doing so, they create transverse waves. When people hear sounds, their ears are sensitive to the pressure differences and interpret the waves as different tones.

Transverse Waves: A wave in which the particles of the medium vibrate up and down ‘at right angles’ to the direction in which the wave is moving. These waves are produced only in a solids and liquids but not in gases.These waves travel in the form of crests and troughs.If a transverse wave is moving in the positive x-direction, its oscillations are in up and down directions that lie in the y–z plane. Light is an example of a transverse wave. For transverse waves in matter, the displacement of the medium is perpendicular to the direction of propagation of the wave. A ripple on a pond and a wave on a string are easily visualized transverse waves.

Transverse waves are waves that are oscillating perpendicularly to the direction of propagation

Q11) What do you meant by logarithmic decrement?

A11) The most convenient way to determine the amount of damping present in a system.is to measure the rate at which amplitude of oscillation dies away. Let us consider the damped vibration shown graphically in Figure 7. Let a0 and al be the first two successive amplitudes of oscillation separated by one period.

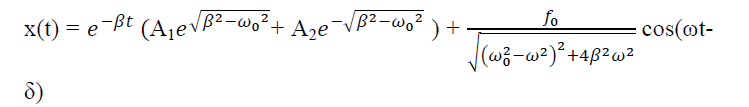
Figure 7: A damped oscillation. The first two amplitudes arc ao and at

You, will note that these amplitudes lie in the same direction /quadrant. If Tis the period of oscillation, then for a weakly damped oscillator, we can write

   ………(1)

You will note that in the ratio a0/ a1, the larger amplitude is in the numerator. That is why this ratio is called the decrement. It is denoted by the symbol d.

You may now ask: Is the decrement same for any two consecutive amplitudes? The answer is: yes, it is.

To show this Ict us consider the ratio of the second and the third ampIitudes. These are observed for t = Tand t = 2T. Then, we can write

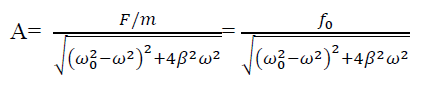   ………(2)

So, we may conclude that for any two consecutive amplitudes seprated. by one period, we have

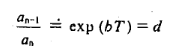      ………(3)

That is, decrement is the same for two successive amplitudes and we can write

   ………(4)

The logarithm of the ratio of successive amplitudes of oscillation separated by one period is called the logarithmic decrement. It is usually denoted by the symbol λ:

     ………(5)

This equation shows that we can measure λ by knowing two successive amplitudes. But from an experimental point of view it is more convenient and accurate to compare amplitudes of oscillations separated by n periods. That is, we measure ao/an. To compute this ratio, we first invert Eq. (5) to write

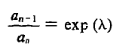
The ratio ao/ancan now be written as

Since the ratio of any two consecutive amplitudes is the same. Taking log of both sides, we get the required result:

This shows that if we plot In(ao/an) versus n for different values of n, we will obtain a straight line. The slope of the line gives us λ.

Q12) What do you meant by relaxation time?

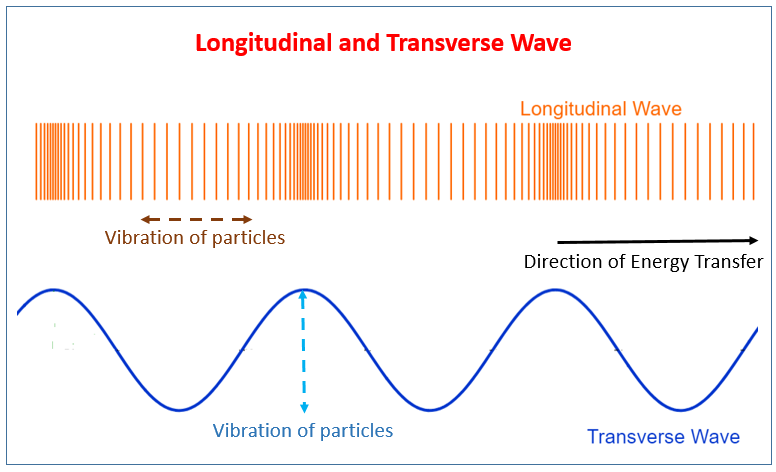
A12) In physics we often measure decay of a quantity in terms of the fraction e-1 of the initial value. This give us another way of expressing the damping effect by means of the time taken by the amplitude to decay to e-1 = 0.368 of its original value. This time is called the relaxation rime. To understand this, we recall that the amplitude of a damped oscillation is given by

If we denote the amplitude of oscillation after an interval of time by a (t+), we can write

By taking the ratio a (t + 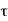)/ a (t), we obtain

This shows that for b =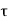-1the amplitude drops to l/e = 0.368 of its initial value. The relaxation time, T, is therefore a measure of the rapidity with which motion is damped.

Q13) Discuss coupled oscillation, normal coordinates and normal frequencies, in- phase and out-of-phase oscillation?

A13) Many important physics systems involved coupled oscillators. Coupled oscillators are oscillators connected in such a way that energy can be transferred between them. The motion of coupled oscillators can be complex, and does not have to be periodic.

However, when the oscillators carry out complex motion, we can find a coordinate frame in which each oscillator oscillates with a very well defined frequency.

A solid is a good example of a system that can be described in terms of coupled oscillations. The atoms oscillate around their equilibrium positions, and the interaction between the atoms is responsible for the coupling.

Many physical systems require more than one variable to quantify their configuration; for example a circuit may have two connected current loops, so one needs to know what current is flowing in each loop at each moment.

Another example is a set of N coupled pendula each of which is a one-dimensional oscillator. A set of differential equations one for each variable will determine the dynamics of such a system.

For a system of N coupled 1-D oscillators there exist N normal modes in which all oscillators move with the same frequency and thus have fixed amplitude ratios (if each oscillator is allowed to move inx dimensions, then  xN normal modes exist). The normal mode is for whole system.

Even though uncoupledangular frequencies of the oscillators are not the same, the effect of coupling is that allbodies can move with the same frequency. If the initial state of the system corresponds tomotion in a normal mode then the oscillations continue in the normal mode.

However ingeneral the motion is described by a linear combination of all the normal modes; since thedifferential equations are linear such a linear combination is also a solution to the coupledlinear equations.

A normal mode of an oscillating system is the motion in which all parts of the systemmove sinusoidally with thesame frequencyand with afixed phase relation.

The best way to illustrate the existence and nature of normal modes is to workthrough some examples, and to see what kind of motion is produced.

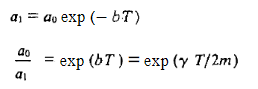
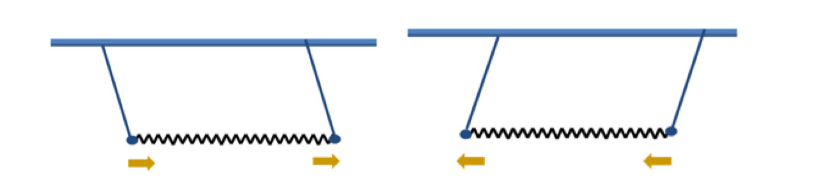
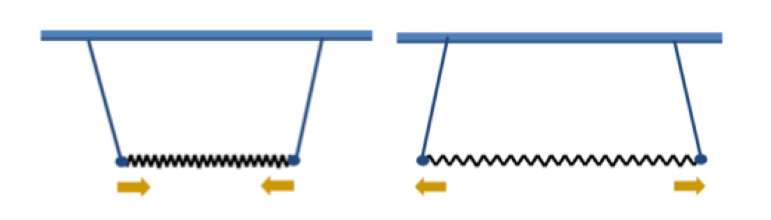
Figure 11: The Coupled Pendulum

We have two identical pendulums (length L) for which we consider small oscillations. In order to find what is the simplest motion, we imagine two experiments:

1) If we draw the two masses aside some distance and release them simultaneously from rest, they will swing in identical phase with no relative change in position. The spring will remain unstretched (or uncompressed) and will exert no force on either mass.We call this vibration pattern the first mode of vibration of the system.

Figure: 12

2) The other obvious way of starting a symmetric oscillation will be to stretch the spring from both ends. If we release the masses from rest simultaneously, we may notice that:

a)The spring now exerts forces during motion

b)From symmetry of motions of A and B, their positions are mirror images of each other

Figure:13

Rather than a single pendulum, now let us consider two pendula which are coupled togetherby a spring which is connected to the masses at the end of two thin strings. The spring hasa spring constant ofkand the length,lof each string is the same, as shown in Figure. 11

Unlike the simple pendulum with a single string and a single mass, we now have todefine the equation of motion of the whole system together. However, we do this in exactlythe same way as we would in any simple pendulum.

We first determine the forces acting on the first mass (left hand side). Like in thesimple pendulum case, we assume that the displacements form the equilibrium positionsare small enough that the restoring force due to gravity is approximately given bymgtanθand acts along the line of masses. This force related to gravity produces the oscillatorymotions if the pendulum is offset from the equilibrium position, i.e

   ………..(1)

Likewise, for the second mass

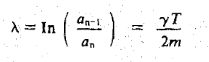   ………..(2)

However, in addition to this gravitational force we also have the force due to the spring that is connected to the masses. This spring introduces additional forces on the two masses, with the force acting in the opposite direction to the direction of the displacement, if we assume that the spring obeys Hooke’s law. Therefore, the equations of motion become modified:

     ………..(3)

And

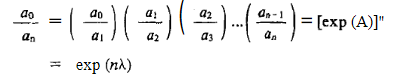     ………..(4)

We now have two equations and two unknowns. To solve these equation by Decoupling Method

The first method is quick and easy, but can only be used in relativelysymmetricsystems,e.g. wherelandmare the same, as in this case. The underlying strategy of this method isto combine the equations of motion given in Equation (3) and (4)in ways so thatxandyonlyappear in unique combinations.

In this problem we can simply try adding the equations of motion, which is one ofthe two useful combinations that we will come across.

………..(5)

This type of equation should look familiar, where the left-hand side is a second derivative of the displacement with respect to time, and the right-hand side is a constant multi-plied by a displacement inxandy. It becomes more clear if we define

Equation (5) becomes,

This is now easily recognisable as the the usual SHM equation, with = ω2q1where

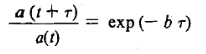
Figure 14: The centre of mass motion of the coupled pendulum as described by q1=x+y.

Figure showing in phase mode..

We can then immediately write a solution for the system as

Where A1 andϕ1are arbitrary constants set by the initial or boundary conditions.

The motion described byq1=x+ytells us about the coupled motion of the twopendula in terms of how they oscillate together around a centre of mass. There is nodependence on the spring whatsoever, asω1does not have a term which involvesk.Thismotion can be visualised as shown in

Given what we have learnt, the obvious other combination ofxandyis to subtractEq. 3  from Eq. 4:

Now let us define

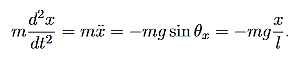
This gives us the following,

We have SHM again, but this time with theq2coordinate, with = ω2q2 , where in this case

Figure 15: The relative motion of the coupled pendulum as described by q2 =x –y

Above Figure shows out of  phase mode.

Again, we can write a solution immediately as

With A2 andϕ2 are arbitrary constants defined by the initial or boundary conditions.

In this case theq2represents the relative motion of the coupled pendulum. As should be clear from the dependence of ω2on the spring constant, this motion must describe howthe motion of the system depends on the compression and expansion of the spring.

The variablesq1andq2are themodesornormal coordinatesof the system. Inany normal mode, only one of these coordinates is active at any one time.

It is actually more common to define the normal coordinates with a normalising factor 1/, such that

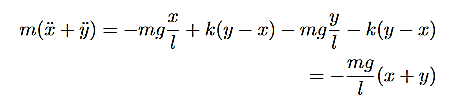
The factor of 1/ is chosen to give standard form for the kinetic enery in terms of the normal modes.

We now have the two normal modes that describe the system, and the general solutionof the coupled pendulum is just the sum of these two normal modes.

which leads to,

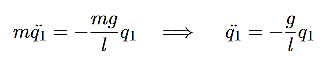
And

which leads to,

The constant are then just set by the initial conditions.

Q14)  Derive wave equation?

A14) WAVE EQUATION

We apply Newton’s law to an elastic string, concluding that small amplitude transverse vibrations of the string obey the wave equation. Consider a tiny element of the string.

Figure:20

The basic notation is

u(x, t) = vertical displacement of the string from the x axis at position x and time t

θ(x, t) = angle between the string and a horizontal line at position x and time t

T(x, t) = tension in the string at position x and time t

ρ(x) = mass density of the string at position x

The forces acting on the tiny element of string are

(a) Tension pulling to the right, which has magnitude T(x+ ∆x, t) and acts at an angle θ(x+ ∆x, t) above horizontal

(b) Tension pulling to the left, which has magnitude T(x, t) and acts at an angle θ(x, t) below horizontal and, possibly,

(c) Various external forces, like gravity. We shall assume that all of the external forces act vertically and we shall denote by F(x, t)∆x the net magnitude of the external force acting on the element of string. The mass of the element of string is essentially.

The mass of the element of string is essentially ρ(x)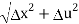 so the vertical component of Newton’s law says that

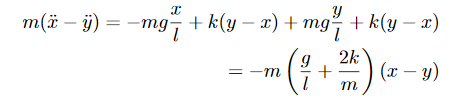
Dividing by ∆x and taking the limit as ∆x→0 gives

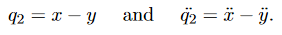
…………(1)

We can dispose of all the θ’s by observing from the figure that

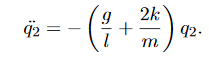
which implies, using the figure on the right below, that

Substituting these formulae into (1) give a horrendous mess. However, we can get considerable simplification by looking only at small vibrations. By a small vibration, we mean that |θ(x, t)| ≪1 for all x and t. This implies that |tanθ(x, t)| ≪1, hence that ∣∣∂u/∂x(x, t)∣∣≪1 and hence that

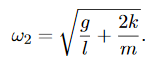
…………(2)

Substituting these into equation (1) give

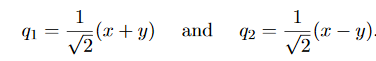
…………(3)

which is indeed relatively simple, but still exhibits a problem. This is one equation in the two unknowns u and T.

Fortunately there is a second equation lurking in the background, that we haven’t used. Namely, the horizontal component of Newton’s law of motion. As a second simplification, we assume that there are only transverse vibrations. Our tiny string element moves only vertically. Then the net horizontal force on it must be zero. That is,

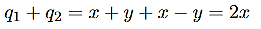
Dividing by ∆x and taking the limit as ∆x tends to zero gives

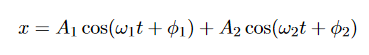
For small amplitude vibrations, cosθ is very close to one and ∂T/∂x(x, t) is very close to zero. In other words T is a function of t only, which is determined by how hard you are pulling on the ends of the string at time t. So for small, transverse vibrations, (3) simplifies further to

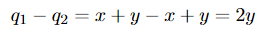
In the event that the string density ρ is a constant, independent of x, the string tension T(t) is a constant independent of t(in other words you are not continually playing with the tuning pegs) and there are no external forces F we end up with

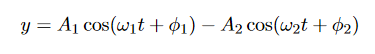
Where

C =