Module-1

Matrix Algebra

Q1: If then prove that

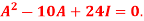
A1:

Here,

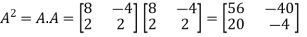
Then-

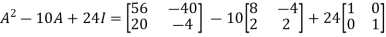
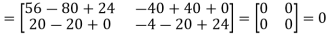
Q2: check whether the following matrix A is symmetric or not?

A =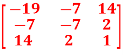 

A2:

As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.

So that, first we will find its transpose,

Transpose of matrix A ,

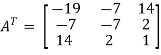
Here,

                                   A =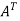

So that, the matrix A is symmetric.

Q3: Find the rank of a matrix M  by echelon form.

M = 

A3:

First we will convert the matrix M into echelon form,

M =

Apply, 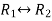, we get

M =

Apply 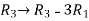 , we get

M =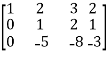

Apply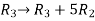 

M =

We can see that, in this echelon form of matrix, the number of non – zero rows is 3.

So that the rank of matrix X will be 3.

Q4: Find the rank of a matrix A by echelon form.

A =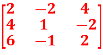

A4:

Convert the matrix A into echelon form,

A =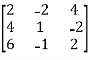

Apply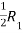 

A =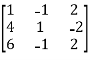

Apply 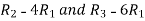   , we get

A =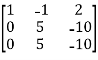

Apply 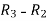, we get

A =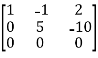

Apply ,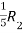

A =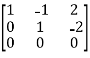

Apply  ,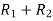

A =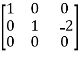

Therefore the rank of the matrix will be 2.

Q5: Find the rank of a matrix A by echelon form.

A =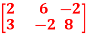

A5:

Transform the matrix A into echelon form, then find the rank,

We have,

A =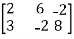

Apply,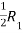 

A =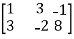

Apply ,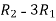

A =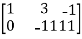

Apply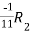

A =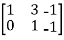

Apply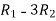

A =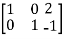

Hence the rank of the matrix will be 2.

Q6: Find the inverse of matrix ‘A’ by using elementary transformation-

A =

A6:

Write the matrix ‘A’ as-  

A = IA

Apply 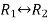, we get

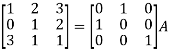
Apply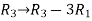

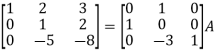
Apply

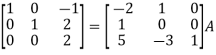
Apply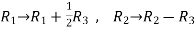

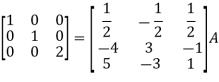
Apply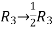

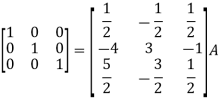
So that,

  =

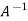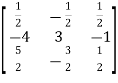
Q7: Find the inverse of matrix ‘A’ by using elementary transformation-

A =

A7:

Write the matrix ‘A’ as-  

A = IA

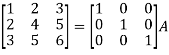
Apply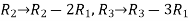

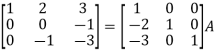
Apply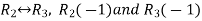

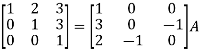
Apply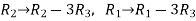

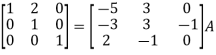
Apply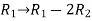

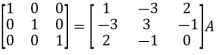
Then-

  =

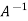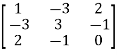
Q8: Are the vectors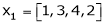,,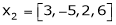 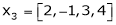linearly dependent. If so, express x1 as a linear combination of the others.

A8:

Consider a vector equation,

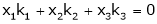
i.e.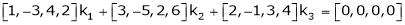

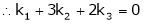
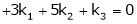
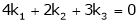
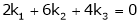
Which can be written in matrix form as,

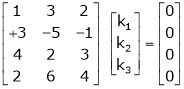
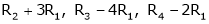
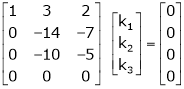
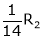
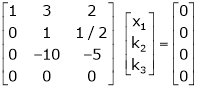
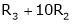
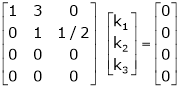
Here 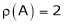& no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

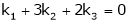
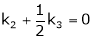
Put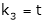

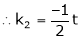and

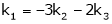
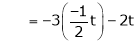
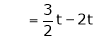
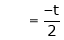
Thus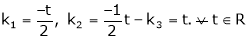

i.e.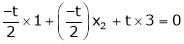

i.e.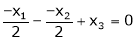

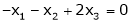
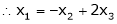
Since F11k2, k3 not all zero. Hence 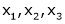are linearly dependent.

Q9: At what value of P the following vectors are linearly independent.

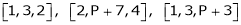
A9:

Consider the vector equation.

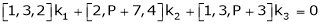
i.e.

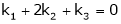
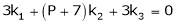
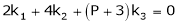
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.

If and only if Determinant of coefficient matrix is non zero.

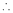consider .

.

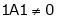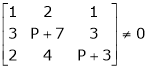i.e.

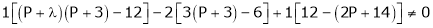
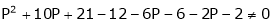
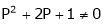
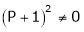
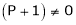
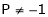
Thus for the system has only trivial solution and Hence the vectors are linearly independent.