Module-2

Eigen values and eigen vectors

Q1: Find the sum and the product of the Eigen values of ?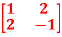

A1:

The sum of Eigen values =  the sum of the diagonal elements

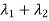   =1+(-1)=0

     The product of the Eigen values is the determinant of the matrix

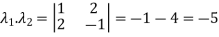
       On solving above equations we get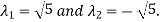

Q2: Find out the Eigen values and Eigen vectors of

A2:
Let A =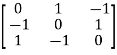

The characteristics equation of A is .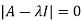

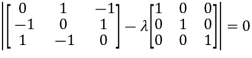
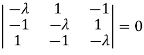
                                           Or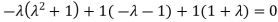 

                                                Or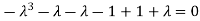 

                                                      Or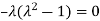

                                                       Or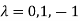

The Eigen vector corresponding to Eigen value 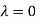is

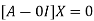
Where X is the column matrix of order 3 i.e.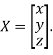

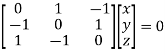
         Or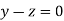

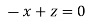
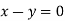
On solving we get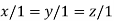 

Thus the Eigen vectors corresponding to the Eigen value 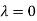is (1,1,1).

The Eigen vector corresponding to Eigen value 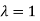is

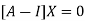
Where X is the column matrix of order 3 i.e.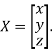

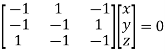
Or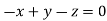    

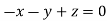
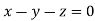
On solving 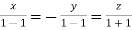or .

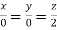Thus the Eigen vectors corresponding to the Eigen value 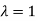is (0,0,2).

The Eigen vector corresponding to Eigen value 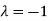is

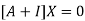
Where X is the column matrix of order 3 i.e.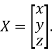

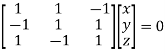
   Or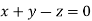    

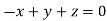
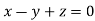
On solving we get 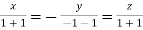 or .

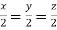Thus the Eigen vectors corresponding to the Eigen value 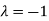is (2,2,2).

Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).

Q3: Find the Eigen values of Eigen vector for the matrix.

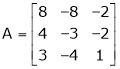
A3:

Consider the characteristic equation as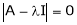

i.e.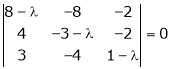

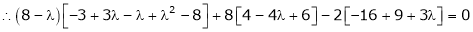
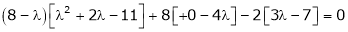
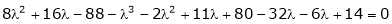
i.e.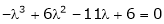

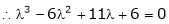
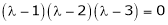
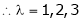are the required eigen values.

Now consider the equation

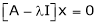       … (1)

Case I:

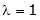Equation (1) becomes,

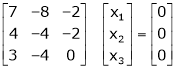
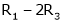
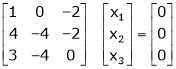
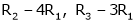
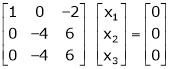
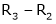
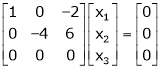
Thus 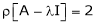and n = 3

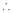3 – 2 = 1 independent variables.

Now rewrite the equations as,

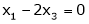
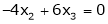
Put

,

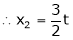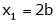
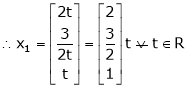
I.e.

the Eigen vector for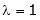

Case II:

If 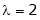equation (1) becomes,

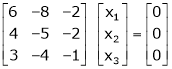
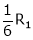
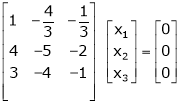
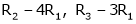
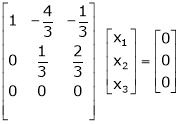
Thus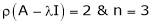

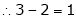
Independent variables.

Now rewrite the equations as,

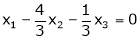
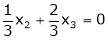
Put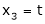

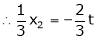
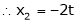
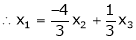
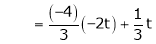
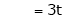
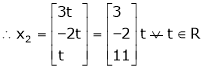
Is the Eigen vector for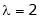

Now

Case III:-

If 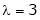equation (1) gives,

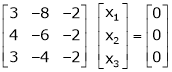
R1 – R2

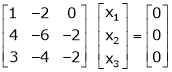
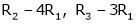
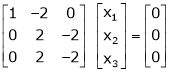
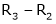
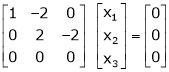
Thus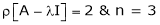

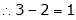
Independent variables

Now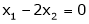

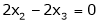
Put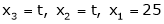

Thus

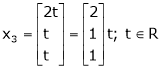
Is the Eigen vector for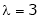

Q4: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.

A4:

Suppose A is any square matrix .

Then,

A =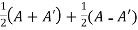

Now,

(A + A’)’ = A’ + A

A+A’ is a symmetric matrix.

Also,

(A - A’)’ = A’ – A

Here A’ – A is an anti – symmetric matrix

So that,

Square matrix = symmetric matrix + anti-symmetric matrix

Q5: prove Q= 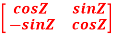is an orthogonal matrix

A5:
Given Q =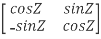

So, QT = 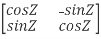…..(1)

Now, we have to prove QT = Q-1

Now we find Q-1

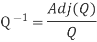
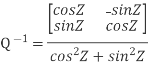
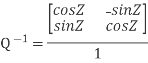
Q-1 = 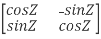… (2)

Now, compare (1) and (2) we get QT = Q-1

Therefore, Q is an orthogonal matrix.

Q6: Express the matrix A as sum of hermitian and skew-hermitian matrix where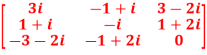

A6:

Let A =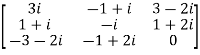

Therefore 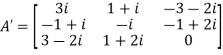   and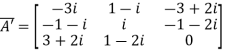

        Let

Again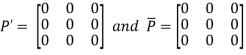

Hence P is a hermitian matrix.

Let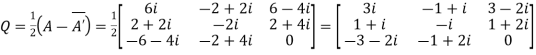 

 Again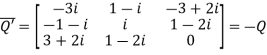

Hence Q is a skew- hermitian matrix.

We Check

  P +Q=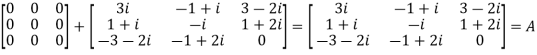

Hence proved.

Q7: Diagonalise the matrix

A7:

Let A=

The three Eigen vectors obtained are  (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .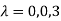

Then 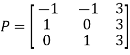   and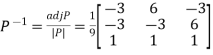

Also we know that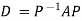    

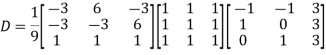
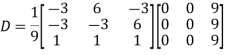
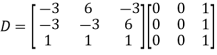
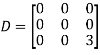
Q8: Diagonalise the matrix

A8:
Let A =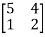

The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values .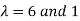

Then 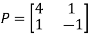   and also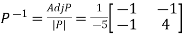 

Also we know that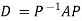    

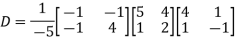
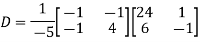
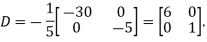
Q9: Write down the properties of Eigen vector.

A9:

Properties of Eigen vector:-

Q10: Write down the properties of Eigen values.

A10:

Properties of Eigen values:-

If

are n Eigen values of square matrix A then

are m Eigen values of a matrix A-1.