Introduction
Q1) What are the Basic Terminologies of Elementary Data Organizations?
A1) Data: Data are simply valuing or set of values
Data Items: It refers to single unit of values.
Data items are divided into sub-items called Group items.
Ex: Employee Name may be divided into three subitems
First name, Middle name, Last name.
Data items that are not further divided into sub items are called Elementary items.
Entity: An entity is something that has attributes or properties which may be assigned values. The values may be numeric or non-numeric.
Ex: Attributes Names Age Sex SSN
Values Rohland Gail 34 F 134-34-5533
Entities with similar attributes form entity set. Each attribute of an entity set has range of values the set of all possible values that could be assigned to particular attribute.
Field: is a single elementary unit of information representing an attribute of an entity.
Record: It is a collection of field values of the given entity.
File: is the collection of records of entities in a given entity set.
Each record in a file may contain field items but the value in a certain field may uniquely determine the record in the file. Such a field k is called the primary key and the values k1, k2….kn are called the keys or key values.
Records may also be classified according to length
A file can have fixed-length records or variable length records.
In fixed length records all the records contain the same data items with the same amount of space assigned to each data item.
In variable length records the file records may contain different lengths.
Example:
Student records have variable lengths since different students take different number of courses. Variable length records have a minimum and maximum length
The above organization of data into fields, records and files may not be complex enough to maintain and efficiently process certain collections of data. For this reason, data are also organized into more complex types of structures.
Q2) Define Insertion operation? With an example?
A2) Insert operation is to insert one or more data elements into an array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array.
Here, we see a practical implementation of insertion operation, where we add data at the end of the array −
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
main() {
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
n = n + 1;
while( j >= k) {
LA[j+1] = LA[j];
j = j - 1;
}
LA[k] = item;
printf("The array elements after insertion :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
When we compile and execute the above program, it produces the following result −
Output
The original array elements are:
LA [0] = 1
LA [1] = 3
LA [2] = 5
LA [3] = 7
LA [4] = 8
The array elements after insertion:
LA [0] = 1
LA [1] = 3
LA [2] = 5
LA [3] = 10
LA [4] = 7
LA [5] = 8
Q3) Define Deletion operation? With an example?
A3) Deletion refers to removing an existing element from the array and re-organizing all elements of an array.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the Kth position of LA.
1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA [J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop
Example
Following is the implementation of the above algorithm −
#include <stdio.h>
void main() {
int LA[] = {1,3,5,7,8};
int k = 3, n = 5;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
j = k;
while( j < n) {
LA[j-1] = LA[j];
j = j + 1;
}
n = n -1;
printf("The array elements after deletion :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
When we compile and execute the above program, it produces the following result −
Output
The original array elements are:
LA [0] = 1
LA [1] = 3
LA [2] = 5
LA [3] = 7
LA [4] = 8
The array elements after deletion:
LA [0] = 1
LA [1] = 3
LA [2] = 7
LA [3] = 8
Q4) Define Traversal operation? With an example?
A4) Each element of an array is accessed precisely once for processing during an array traversal operation.
This is also known as array visiting.
As an illustration
Let LA be an unordered Linear Array with N item.
/Create a programme to perform a traversal operation.
void main #include stdio.h> ()
{
int LA[] = {2,4,6,8,9};
int i, n = 5;
printf("The array elements are:\n");
for(i = 0; i < n; i++)
{
printf("LA[%d] = %d \n", i, LA[i]);
}
}
Output
The original array elements are:
LA [0] = 2
LA [1] = 4
LA [2] = 6
LA [3] = 8
LA [4] = 9
Q5) What are the Analysis of an Algorithm? In brief.
A5) Analysis is the theoretical way to study performance of computer program. Analysis of an algorithm is helpful to decide the complexity of an algorithm. There are three ways to analyze an algorithm which are stated as below.
1. Worst case: In worst case analysis of an algorithm, upper bound of an algorithm is calculated. This case considers the maximum number of operations on algorithm. For example, if user want to search a word in English dictionary which is not present in the dictionary. In this case user has to check all the words in dictionary for desired word.
2. Best case: In best case analysis of an algorithm, lower bound of an algorithm is calculated. This case considers the minimum number of operations on algorithm. For example, if user want to search a word in English dictionary which is found at the first attempt. In this case there is no need to check other words in dictionary.
3. Average case: In average case analysis of an algorithm, all possible inputs are considered and computing time is calculated for all inputs. Average case analysis is performed by summation of all calculated value which is divided by total number of inputs. In average case analysis user must be aware about the all types of input so average case analysis are very rarely used in practical cases.
Q6) Define Asymptotic Notations?
A6) To express the running time complexity of algorithm three asymptotic notations are available. Asymptotic notations are also called as asymptotic bounds. Notations are used to relate the growth of complex function with the simple function. Asymptotic notations have domain of natural numbers.
Q7) Describe Big-oh notation?
A7) Big-oh notations can be express by using ‘o’ symbol. This notation indicates the maximum number of steps required to solve the problem. This notation expresses the worst-case growth of an algorithm. Consider the following diagram in which there are two functions f(x) and g(x). f(x) is more complex than the function g(x).
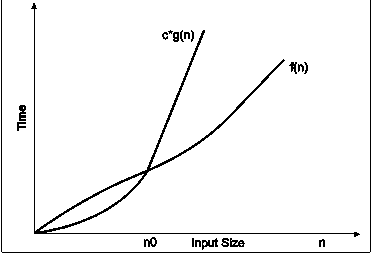
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always greater than f(n).
Now f(n)=Og(n)if there is some constant ‘c’ and some initial value ‘n0’. such that f(n)<=c*g(n) for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
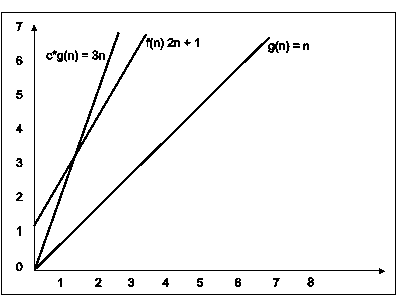
In the above example g(n) is ‘’n’ and f(n) is ‘2n+1’ and value of constant is 3. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always greater than f(n) for constant ‘3’. We can write the conclusion as follows
f(n)=O g(n) for constant ‘c’ =3 and ‘n0’=1
such that f(n)<=c*g(n) for all n>n0
Q8) Define Big-omega notation?
A8) Big-omega notations can be express by using ‘Ω’ symbol. This notation indicates the minimum number of steps required to solve the problem. This notation expresses the best-case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
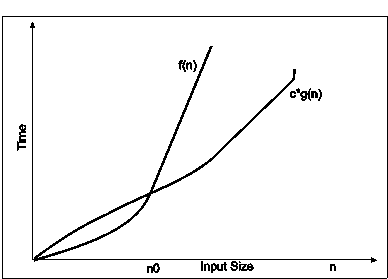
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always smaller than f(n).
Now f(n)=Ωg(n)if there is some constant ‘c’ and some initial value ‘n0’. such that c*g(n) <= f(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
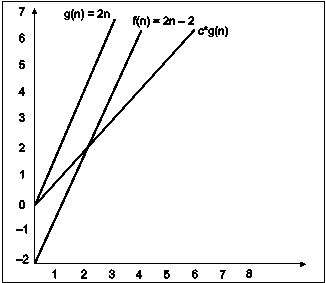
In the above example g(n) is ‘2n’ and f(n) is ‘2n-2’ and value of constant is 0.5. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always smaller than f(n) for constant ‘0.5’. We can write the conclusion as follows
f(n) = Ω g(n) for constant ‘c’ =0.5 and ‘n0’=2
such that c*g(n)<= f(n) for all n>n0
Q9) Define Big-theta notation?
A9) Big-theta notations can be express by using ‘Ɵ’ symbol. This notation indicates the exact number of steps required to solve the problem. This notation expresses the average case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
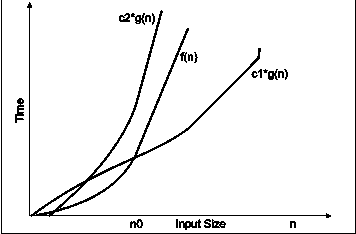
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c1 and c2 which bound function f(n) at some point n0. Beyond the point ‘n0’ function c1*g(n) is always smaller than f(n) and c2*g(n) is always greater than f(n).
Now f(n) = g(n) if there is some constant ‘c1 and c2’ and some initial value ‘n0’. such that c1*g(n) <= f(n)<=c2*g(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
f(n) = g(n) if and only if f(n)=O g(n) and f(n)=Ω g(n)
Consider the following example
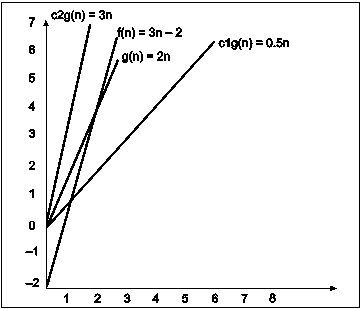
In the above example g(n) is ‘2n’ and f(n) is ‘3n-2’ and value of constant c1 is 0.5 and c2 is 2. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c1*g(n) is always smaller than f(n) for constant ‘0.5’ and c2*g(n) is always greater than f(n) for constant ‘2’. We can write the conclusion as follows
f(n)=Ω g(n) for constant ‘c1’ =0.5, ‘c2’ = 2 and ‘n0’=2
such that c1*g(n)<= f(n)<=c2*g(n) for all n>n0
Q10) What do you mean by Time-Space trade off?
A11) Time complexity is about to number of times compiler execute basic operations in instruction. That is because basic operations are so defined that the time for the other operations is much less than or at most proportional to the time for the basic operations. To determine time complexity user, need to calculate frequency count and express it in terms of notations. Total time taken by program is the summation of compile time and running time. Out of these two main point to take care about is running time as it depends upon the number and magnitude of input and output.
Q12) Define Space complexity?
A12) Space complexity is about to maximum amount of memory required for algorithm. To determine space complexity user, need to calculate frequency count and express it in terms of notations.
Frequency count analysis for this code is as follows
Sr. No. | Instructions | Frequency count |
#include<stdio.h> |
| |
2. | #include<conio.h> |
|
3. | void main() { |
|
4. | int marks; |
|
5. | printf(“enter a marks”); | add 1 to the time count |
6. | scanf(“%d”,&marks); | add 1 to the space count |
7. | printf(“your marks is %d”,marks); | add 1 to the time count |
8. | getch(); } |
|
In the above example, for the first four instructions there is no frequency count. For data declaration and the inclusion of header file there is no frequency count. So, for this example has a frequency count for time is 2 and a frequency count for space is 1. So, total frequency count is 3.
Consider the following example
Sr. No. | Instructions | Frequency count |
#include<stdio.h> |
| |
2. | #include<conio.h> |
|
3. | void main() { |
|
4. | int sum=0; | 1 |
5. | for(i=0;i<5;i++) | 6 |
6. | sum=sum+i; | 5 |
7. | printf(“Addition is %d”,sum); | 1 |
8. | getch(); } |
|
Explanation: In the above example, one is added to frequency count for instruction four and seven after that in fifth instruction is check from zero to five so it will add value six to frequency count. ‘For’ loop executed for five times so for sixth instruction frequency count is five. Total frequency count for above program is 1+6+5+1 =13.
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | void main() { |
|
4. | int a[2][3],b[2][3],c[2][3]] |
|
5. | for(i=0;i<m;i++) | m+1 |
6. | { |
|
7. | for(j=0;j<n;j++) | m(n+1) |
8. | { |
|
9. | c[i][j]=a[i][j]*b[i][j]; | m.n |
10. | }} |
|
11. | getch(); } |
|
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | void main() { |
|
4. | int a[2][3],b[2][3],c[2][3]] |
|
5. | for(i=0;i<m;i++) | m+1 |
6. | { |
|
7. | for(j=0;j<n;j++) | m(n+1) |
8. | { |
|
9. | a[i][j]=n; | m.n |
10. | for(k=0;k<n;k++) | mn(n+1) |
11. | c[i][j]=a[i][j]*b[i][j]; | m.n.n |
12. | }} |
|
13. | getch(); } |
|
Explanation: For above program total frequency count
=(m+1) +m(n+1) +mn+mn(n+1) +mn
=m+1+mn+m+mn+mn2 +mn+mn2
=2 mn2+3mn+2m+1
=mn(2n+3) +2m+1
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | void main() { |
|
4. | int n=1,m; | 1 |
5. | Do |
|
6. | { |
|
7. | printf(“hi”); | 10 |
8. | if(n==10) | 10 |
9. | break; | 1 |
10. | n++; | 9 |
11. | } |
|
12. | while(n<15); | 10 |
13. | getch(); } |
|
Explanation: the above example, one is added to frequency count for instruction four. The loop will execute till value of n is incremented to 10 from 1, so for loop statements i.e., instructions seven and eight is execute for tem times. when the value of ‘n’ is ten then ‘break’ statement will execute for one time and it will skip the tenth execution of tenth instruction. Tenth instruction will add value nine to frequency count. Total frequency count for above program is 10+10+1+9+10 = 40.
Q13) Define Linear Search Techniques and their complexity analysis?
A13) Thus Algorithm for Linear Search is
1. start at one end of the list
2. if the current element is not equal to the search target, move to the next element,
3. stop when a match is found or the opposite end of the list is reached.
Function for Linear search is
find(values, target)
{
for( i = 0; i < values.length; i++)
{
if (values[i] == target)
{ return i; }
}
return –1;
}
If element is found this function returns index of that element otherwise it returns –1.
Example: we have an array of integers, like the following:

Let’s search for the number 7. According to function for linear search index for element 7 should be returned. We start at the beginning and check the first element in the array.
9 | 6 | 7 | 12 | 1 | 5 |
First element is 9. Match is not found and hence we move to next element i.e., 6.
9 | 6 | 7 | 12 | 1 | 5 |
Again, match is not found so move to next element i.e.,7.
9 | 6 | 7 | 12 | 1 | 5 |
0 | 1 | 2 | 3 | 4 | 5 |
We found the match at the index position 2. Hence output is 2.
If we try to find element 10 in above array, it will return –1, as 10 is not present in the array.
Complexity Analysis of Linear Search:
Let us assume element x is to be searched in array A of size n.
An algorithm can be analyzed using following three cases.
1. Worst case
2. Average case
3. Best case
1. Worst case: In Linear search worst case happens when element to be searched is not present. When x is not present, the linear search function compares it with all the elements of A one by one. The size of A is n and hence x is to be compared with all n elements. Thus, the worst-case time complexity of linear search would be O(n).
2. Average case: In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. Following is the value of average case time complexity.
Average Case Time= = = O (n)
3. Best Case: In linear search, the best case occurs when x is present at the first location. So, time complexity in the best-case would-be O (1).
P1: Program for Linear Search
#include<stdio.h>
#include<conio.h>
int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}
int search(int a[],int n,int k)
{
int i;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}
Merits:
Demerits:
Q14) Define Binary Search Techniques and their complexity analysis?
A14) Binary Search requires sorted array.
Steps to perform binary search on sorted array A of size n are as follows.
1. Initialize lower and upper limit of array to be searched Low=0, High= n–1.
2. Find the middle position
Mid= (Low + High)/2
3. Compare the input key value with the key value of the middle element of the array. It has 3 possibilities.
Case 1: If keys match then return mid and print element found.
if(key==A[mid])
return mid
Case 2: If key is less than middle element then element is present in left half of array. Update High and goto step 2.
if(key<A[mid])
High= Mid–1
goto step 2
Case 3: If key is greater than middle element then element is present in right half of array. Update Low and goto step 2.
if(key>A[mid])
Low= Mid+1
goto step 2
Case 4: if (Low>High)
Print element not found.
Iterative algorithm for Binary Search
int BinarySearch(int A[],int x)
{
int mid,n;
int Low = 0;
int High = n–1;
while ( Low <= High )
{
mid = (Low + High) / 2;
if ( A[mid] == x )
return mid;
if ( A[mid] > x )
High = mid – 1;
else Low = mid + 1;
}
return –1;
}