Unit – 4
Sorting and Hashing
Q1) What are the Objective and properties of different sorting algorithms?
A1) Assume we want to sort list in ascending order. Selection sort finds the smallest element from unsorted list and swap it with the element in first position. Then it finds second smallest element and swap it with element at second position. This process is repeated till entire list is sorted in ascending order. Each time we swap elements, we say that we have completed a sort pass. A list of n elements requires n–1 passes to completely rearrange the data.
Procedure for every pass is as follows.
Pass 1: Find the position P of the smallest in the list of N elements A[l], A [2], . . ., A[N], and then interchange A[P] and A [1]. Then A [1] is sorted.
Pass 2: Find the position P of the smallest in the sublist of N –1 element A [2], A [3], . . ., A[N], and then interchange A[P]and A [2]. Then A[l], A [2] is sorted.
Pass 3: Find the position P of the smallest in the sublist of N–2 elements A [3], A [4], . . ., A[N], and then interchange A[P] and A [3]. Then: A[l], A [2], A [3] is sorted.
Pass N –1: Find the position P of the smaller of the elements A [N –1), A[N], and then interchange A[P] and A[N–1]. Then: A[l], A [2], . . ., A[N] is sorted. Thus, A is sorted after N –1 passes.
Example 1:
25 | 79 | 41 | 9 | 34 | 60 |
Fig.: Original List
We will apply selection sort on this list.
Pass 1:
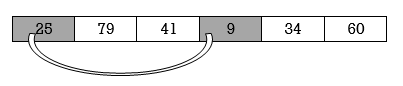
Here smallest element is 9 and 25 is located at first position. so, we swap 9 with 25.
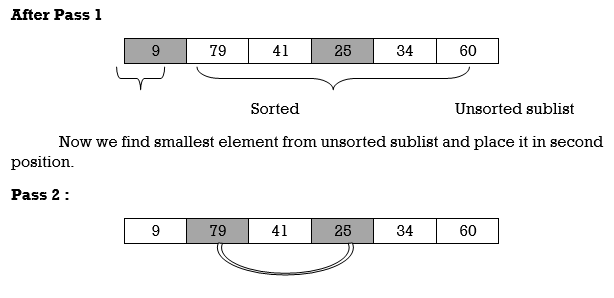
Unsorted sublist has 25 as a smallest element and 79 is located at second position. Hence, we swap 25 and 79.
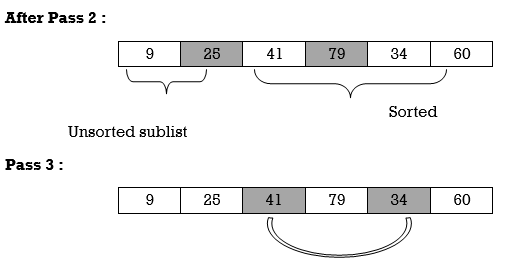
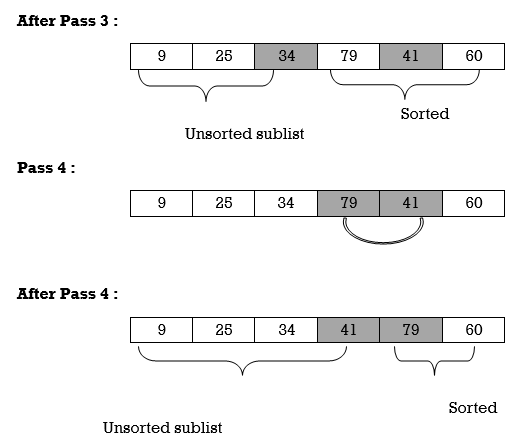
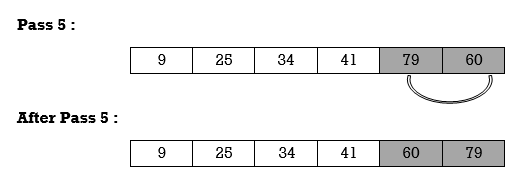
Thus, list is sorted.
We will see one more example.
Apply selection sort on array A= {77,30,40,10,88,20,65,56}
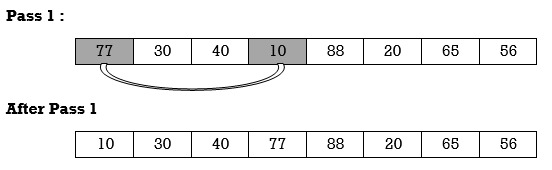
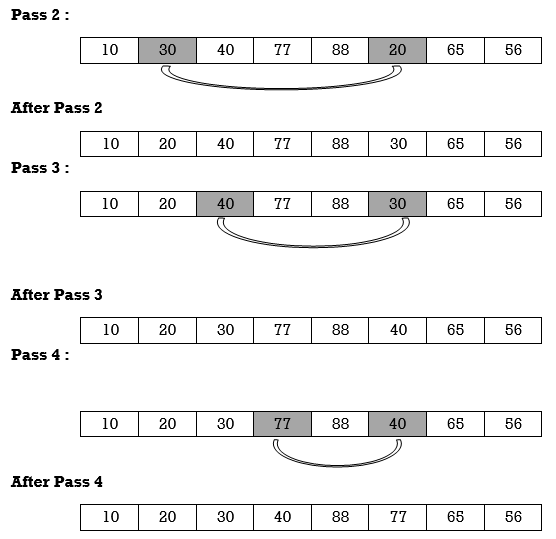
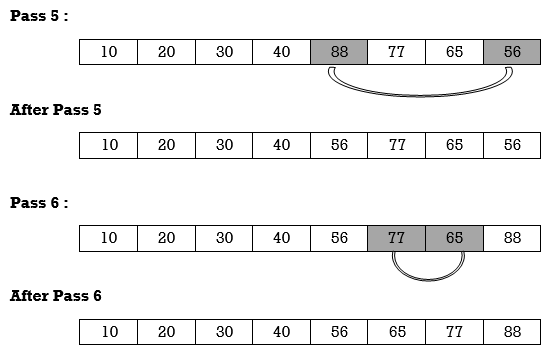
Hence the list is sorted in ascending order by applying selection sort.
Function for Selection Sort
void selectionSort(int A[], int n)
{
int i, j, s, temp;
for (i= 0; i <= n; i ++)
{
s = i;
for (j=i+1; j <= n; j++)
if(A[j] < A[s])
s= j;
// Smallest selected; swap with current element
temp = A[i];
A[i] = A[s];
A[s] = temp;
}
P4: Program to perform Selection Sort.
#include <stdio.h>
int main()
{
int A[100], n, i, j, s, temp;
/* n=total no. of elements in array
s= smallest element in unsorted array
temp is used for swapping */
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for ( i = 0 ; i < n ; i++ )
scanf("%d", &A[i]);
for ( i = 0 ; i < ( n – 1 ) ; i++ )
{
s = i;
for ( j = i + 1 ; j < n ; j++ )
{
if ( A[s] > A[j] )
s = j;
}
if ( s != i )
{
temp = A[i];
A[i] = A[s];
A[s] = temp;
}
}
printf("Sorted list in ascending order:\n");
for ( i = 0 ; i < n ; i++ )
printf("%d\n", A[i]);
return 0;
}
Output:
Enter number of elements
5
Enter 5 integers
4
1
7
5
9
Sorted list in ascending order
1
4
5
7
9
Q2) What are the Complexity of Selection Sort?
A2) In selection sort outer for loop is executed n–1 time. On the kth time through the outer loop, initially the sorted list holds
k–1 elements and unsorted portion holds n–k+1 elements. In inner for loop 2 elements are compared each time.
Thus, 2*(n–k) elements are examined by the inner loop during the kth pass through the outer loop. But k ranges from 1 to n–1.
Total number of elements examined is:
T(n) = 2*(n –1) + 2*(n–2) + 2*(n–3) + ... + 2*(n–(n–2)) + 2*(n–(n–1))
=2*((n–1) + (n–2) + (n–3) + ... + 2 + 1)
(Or 2*(sum of first n–1 integers)
=2*((n–1) *n)/2)
=n2 – n, so complexity of algorithm is O(n2).
Q3) What is Bubble Sort? With an example?
A3) Steps to perform Bubble sort are as follows.
Assume we want to sort the elements in ascending order and no two elements are equal.
1. Compare first element with second element. If first element is greater than next element, we interchange their position accordingly. i.e., first element is moved to second element’s position and second element is moved to first element’s position. If No, then we don’t interchange any elements.
2. The element in second position is compared with element in third position and the process of interchanging elements is performed if second is greater than third element. The whole process of comparing and interchanging is repeated till last element. When the process gets completed, the largest element in array will get placed in the last position of the array.
Let us consider array A of size n. Then Algorithm for Bubble sort is
1. Set i to 0.
2. Set j to 0.
3. if(A[j]>A[j+1])
swap A[j], A[j+1]
4. Increment j
5. if j<(n–1–i) goto step 3
6. Increment i
7. if(i<n–1) goto step 2.

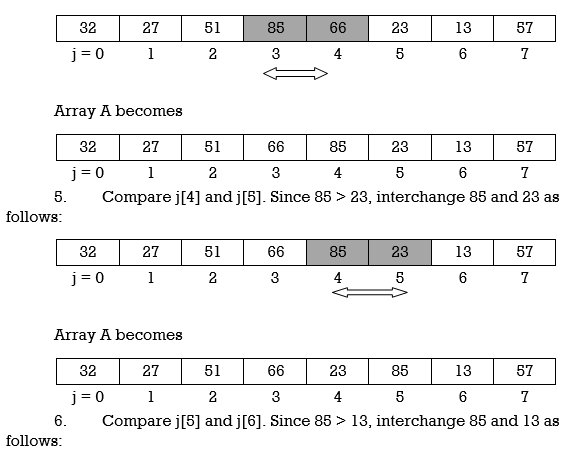
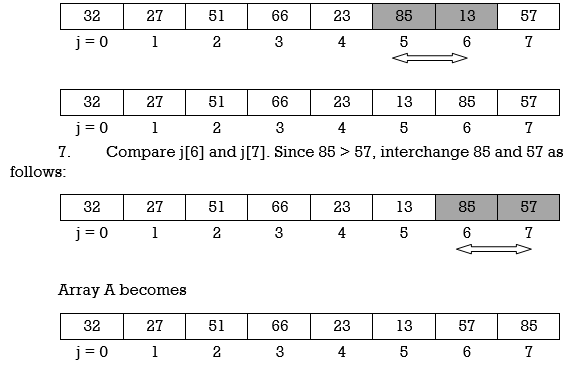
At the end of this first pass, the largest number, 85, has moved to the last position. However, the rest of the numbers are not sorted, even though some of them have changed their positions.
Pass 2 will move second last number at second last position, pass 3 will move third last number at third last position and so on. Here we show array after every pass.
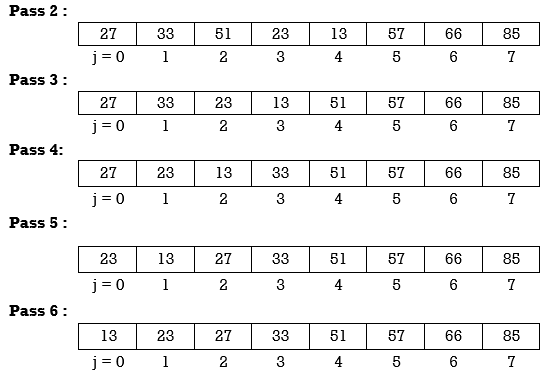
Hence the array is sorted in 6 passes.
We will see one more example
Example 2: Apply Bubble Sort on array A= {5,3,1,9,8,2,4,7}.
j =0 | 5 | 3 | 1 | 9 | 8 | 2 | 4 | 7 |
j =1 | 3 | 5 | 1 | 9 | 8 | 2 | 4 | 7 |
j =2 | 3 | 1 | 5 | 9 | 8 | 2 | 4 | 7 |
j =3 | 3 | 1 | 5 | 9 | 8 | 2 | 4 | 7 |
j =4 | 3 | 1 | 5 | 8 | 9 | 2 | 4 | 7 |
j =5 | 3 | 1 | 5 | 8 | 2 | 9 | 4 | 7 |
j =6 | 3 | 1 | 5 | 8 | 2 | 4 | 9 | 7 |
j =7 | 3 | 1 | 5 | 8 | 2 | 4 | 7 | 9 |
Pass 2: i=2
3 | 1 | 5 | 8 | 2 | 4 | 7 | 9 |
1 | 3 | 5 | 8 | 2 | 4 | 7 | 9 |
1 | 3 | 5 | 8 | 2 | 4 | 7 | 9 |
1 | 3 | 5 | 8 | 2 | 4 | 7 | 9 |
1 | 3 | 5 | 2 | 8 | 4 | 7 | 9 |
1 | 3 | 5 | 2 | 4 | 8 | 7 | 9 |
1 | 3 | 5 | 2 | 4 | 7 | 8 | 9 |
Pass 3:
1 | 3 | 5 | 2 | 4 | 7 | 8 | 9 |
1 | 3 | 5 | 2 | 4 | 7 | 8 | 9 |
1 | 3 | 5 | 2 | 4 | 7 | 8 | 9 |
1 | 3 | 2 | 5 | 4 | 7 | 8 | 9 |
1 | 3 | 2 | 4 | 5 | 7 | 8 | 9 |
Pass 4:
1 | 3 | 2 | 4 | 5 | 7 | 8 | 9 |
1 | 3 | 2 | 4 | 5 | 7 | 8 | 9 |
1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 |
This array gets sorted in 4 passes only.
Example: Apply Bubble Sort on array A= {23,78,45,8,32,56}
Pass 1:
23 | 78 | 45 | 8 | 32 | 56 |
23 | 78 | 45 | 8 | 32 | 56 |
23 | 45 | 78 | 8 | 32 | 56 |
23 | 45 | 8 | 78 | 32 | 56 |
23 | 45 | 8 | 32 | 78 | 56 |
23 | 45 | 8 | 32 | 56 | 78 |
Pass 2:
23 | 45 | 8 | 32 | 56 | 78 |
23 | 45 | 8 | 32 | 56 | 78 |
23 | 8 | 45 | 32 | 56 | 78 |
23 | 8 | 32 | 45 | 56 | 78 |
Pass 3:
23 | 8 | 32 | 45 | 56 | 78 |
8 | 23 | 32 | 45 | 56 | 78 |
This array is sorted in 3 passes.
P3: Write a Program for Bubble sort in C
#include <stdio.h>
#include<conio.h>
void bubble_sort(int A[], int n);
int main()
{
int A[100], n, i, j, swap;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter the elements\n", );
for (i = 0; i < n; i++)
scanf("%d", &A[i]);
bubble_sort(A, n);
printf("Sorted list in ascending order:\n");
for ( i = 0 ; i < n ; i++ )
printf("%ld\n", A[i]);
return 0;
}
void bubble_sort(int A[], int n)
{
int i, j, t;
for (i = 0 ; i < ( n – 1 ); i++)
{
for (j = 0 ; j < (n – i – 1); j++)
{
if (A[j] > list[j+1])
{
/* Swapping */
t = A[j];
A[j] = A[j+1];
A[j+1] = t;
}
}
}
}
Q4) Describe Complexity of Bubble sort?
A4) Suppose we have a list with n elements, and each element perform n – 1 comparison with elements to its left, and swap, if necessary.
Best Case: If the list is already sorted, only one iteration is performed and complexity is O (1).
Average and Worst case: For n elements at most n – 1 swap operations is performed in each pass. The worst and average case complexity is O(n2).
Q5) Define Insertion Sort? With example?
A5) Insertion Sort reads all elements from 1 to n and inserts each element at its proper position. This sorting method works well on small list of elements.
Procedure for each pass is as follows.
Pass 1:
A[l] by itself is trivially sorted.
Pass 2:
A [2] is inserted either before or after A[l] so that: A[l], A [2] is sorted.
Pass 3:
A [3] is inserted into its proper place so that: A[l], A [2], A [3] is sorted.
Pass 4:
A [4] is inserted into its proper place A[l], A [2], A [3], A [4] is sorted.
Pass N: A[N] is inserted into its proper place in so that: A[l], A [ 2], . . ., A [ N] is sorted
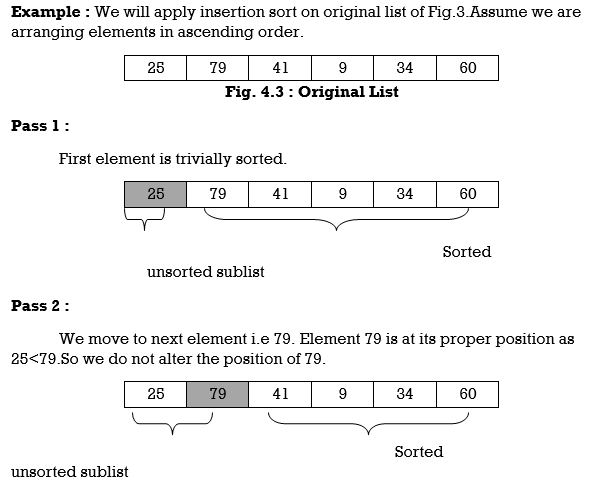
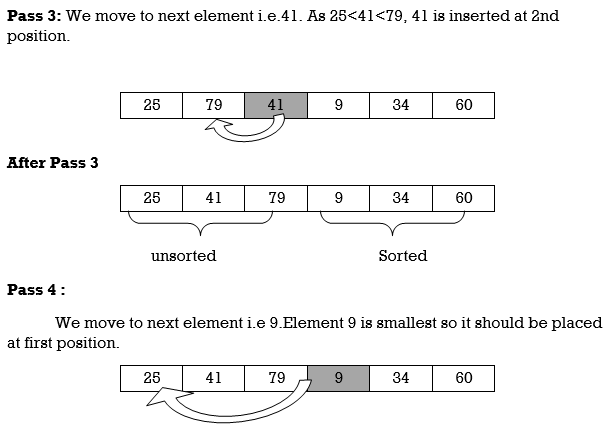
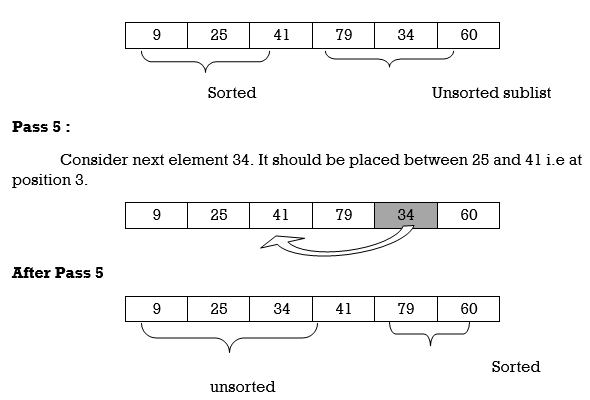
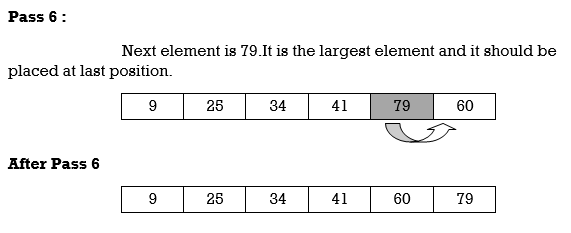
Hence the list is sorted using insertion sort.
We will see one more example.
Apply Insertion sort on array A= {77,30,40,10,88,20,65,56}
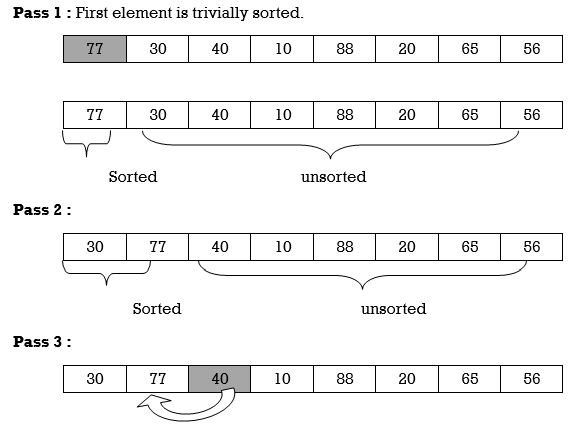
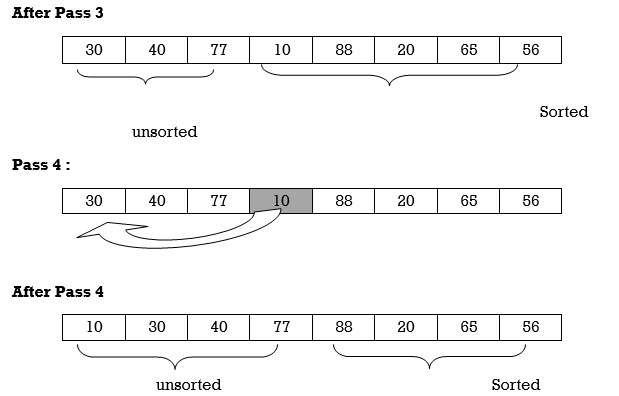
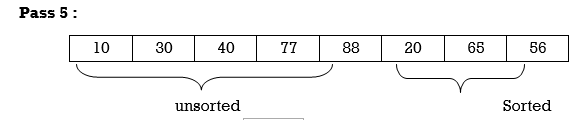
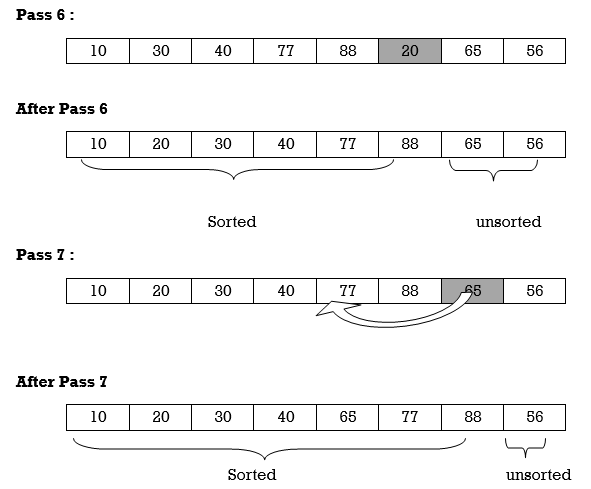
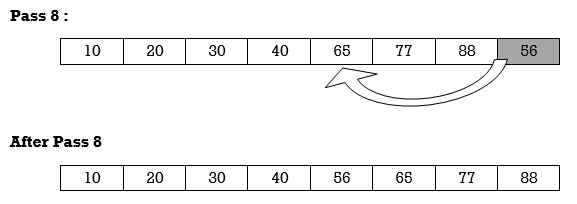
Hence the list is sorted using Insertion sort.
C Function for Insertion Sort
void insertionSort(int A[], int n)
{
int i, p, temp, j;
for (i = 1; i<=n; i++)
{
p= 0;
temp = A[i];
for (j=i–1; j >= 0 && !p;)
if(temp < A[j])
{
A[j + 1]= A[j];
j––;
}
else
p = 1;
A[j + 1] = temp;
}
return;
}
P5: Program to implement insertion sort.
#include <stdio.h>
int main()
{
int n, A[100], i, j, t;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for (i = 0; i < n; i++) {
scanf("%d", &A[i]);
}
for (i = 1 ; i <=( n – 1); i++)
{
j = i;
while ( j > 0 && A[j] < A[j–1])
{
t = A[j];
A[j] = A[j–1];
A[j–1] = t;
j––;
}
}
printf("Sorted list in ascending order:\n");
for (i = 0; i <= n – 1; i++) {
printf("%d\n", A[i]);
}
return 0;
}
Output:
Enter number of elements
5
Enter 5 integers
9
4
2
5
3
Sorted list in ascending order
2
3
4
5
9
Q6) Describe Complexity of Insertion sort?
A6) Worst Case Complexity: In the worst case, for each i we do (i – 1) swaps inside the inner for–loop–therefore, overall number of swaps (when i goes from 2 to n in the outer for loop) is
T(n)=1 + 2 + 3 +...+(I – 1) +.... + n – 1
=n (n – 1)/2
=O(n2)
Average case Complexity is O(n2).
Best Case Complexity is O(n).
Q7) Define Quick Sort? With example?
A7) Quick sort is most efficient method of sorting. It uses divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is pivot element. Index positions of first and last element of array A is denoted by ‘first’ and ‘last’.
1. Initially first=0 and last=n–1.
2. Increment first till A[first]<=p
3. Decrement last till A[last]>=p
4. If first < last then swap A[first] with A[last].
5. If first > last then swap p with A[last] and thus position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is final position of p. Then A [0] to A[j–1] are less than p and A [j + 1] to A [n–1] are greater than p.
6. Now we consider left part of array A i.e. A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply same procedure for right part of array.
7. We continue with above steps till no more partitions can be made for every subarray.
C function for Quick sort
x=0, y=n–1
void Quicksort (A, x, y)
{
if(x<y)
{
first=x;
last=y;
p=A[x];
while(first<last)
{
while(A[first]<p)
first++;
while(A[last]>p)
last ––;
if(first<last)
swap(A[first], A[last])
}
swap(A[x], A[y])
Quicksort (A, x, last–1);
Quicksort (A, first+1, y);
}
We will see examples on Quick sort
Example: Apply Quicksort on array
A= {27,6,39,2,65,12,57,18,49,19}

Now, compare A[last] with p. We decrement last till A[last]>=p.
Here 19 < 27. So, condition A[last]>=p becomes false and we stop decrementing last.
Currently first=2 and last=9.
i.e., first < last so we swap A[first] and A[last]. Swapping 39 and 19 we get
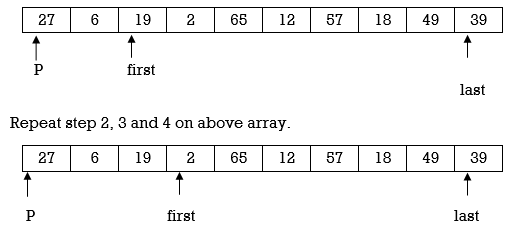
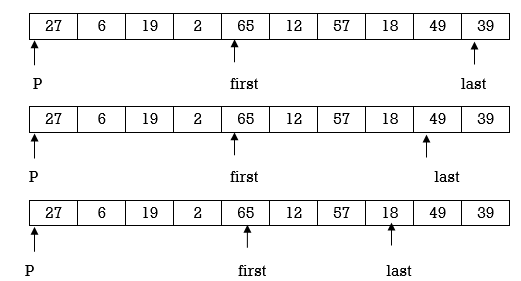
Here again first<last so we swap A[first] and A[last]. Swapping 65 and 18 we get
Repeat step 2,3 and 4.
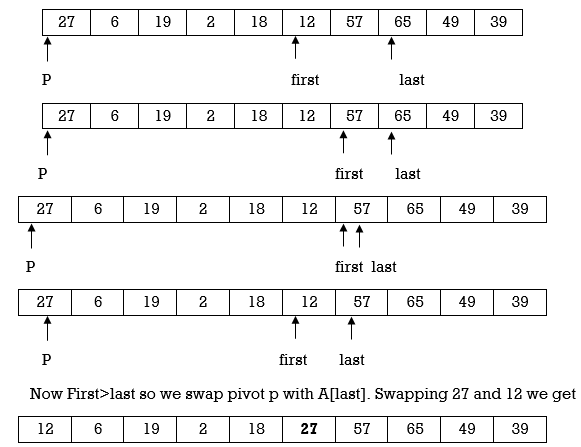
Here we complete Pass 1. Now pivot element is 27 and it divides array in left and right partition. We can see that element less than pivot are in left partition and elements greater than pivot are in right partition.
Now we continue same procedure for left and right partition. Here we see results of corresponding passes.
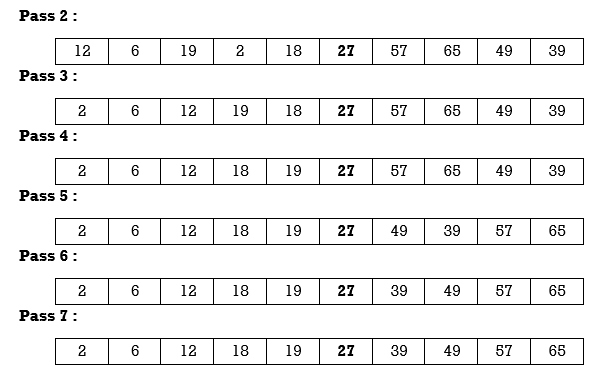
We will see another example.
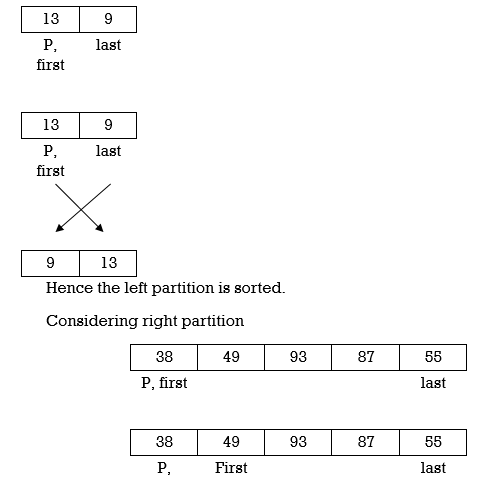
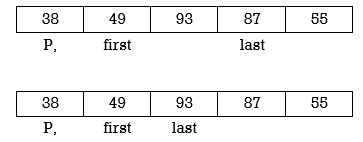
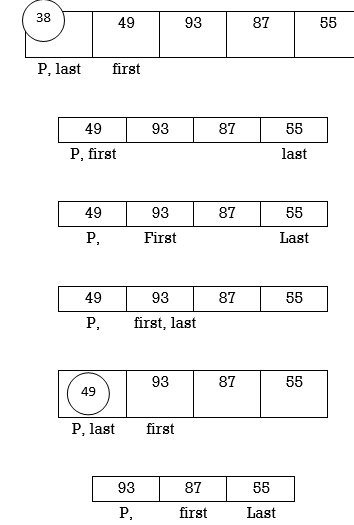
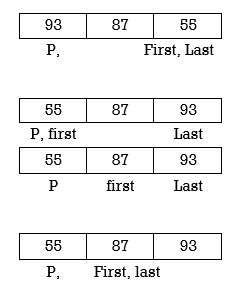
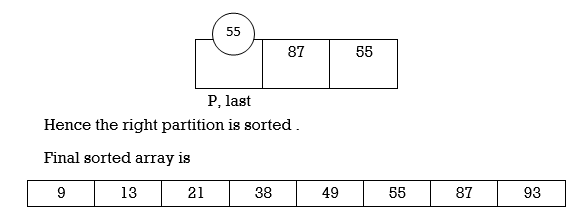
Example: Apply Quicksort on array A= {21,55,49,38,13,93,87,9}
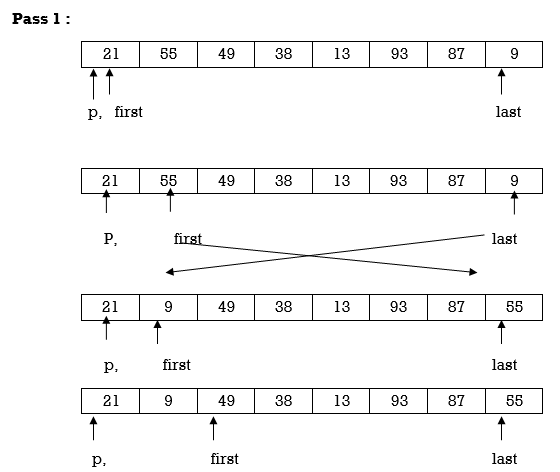
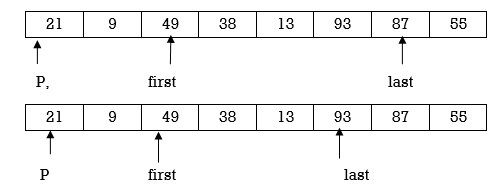
Now first>last hence swap pivot and A[last]. Swapping 21 and 13 we get
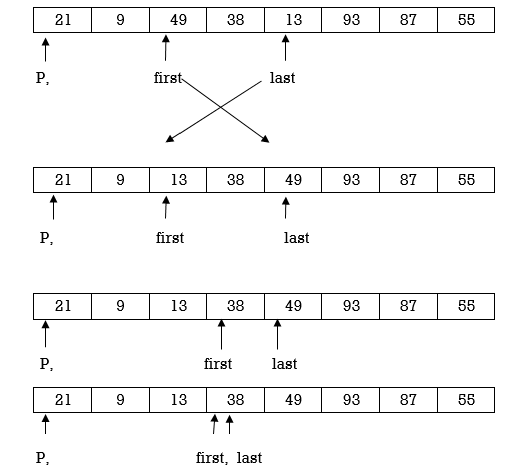
Now first > last hence swap pivot and A [last]’. Swapping 21 and 13 we get
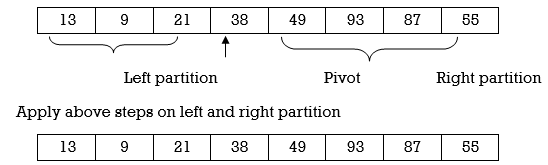
Left Partition
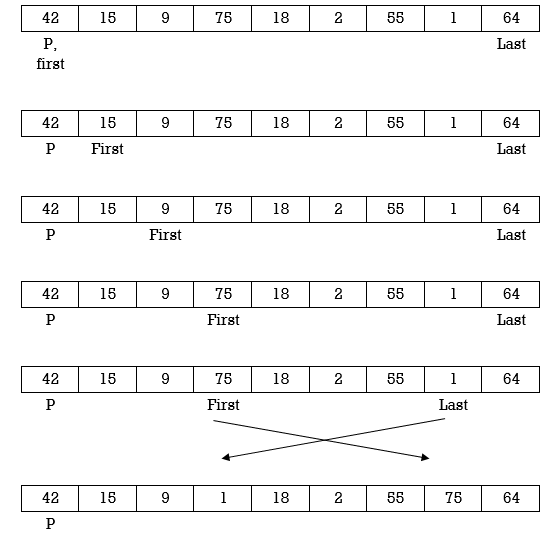
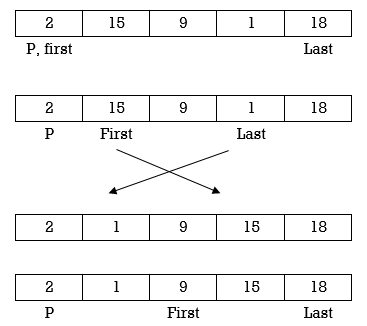
Example: Apply Quick Sort on A= {42,15,9,75,18,2,55,1,64}
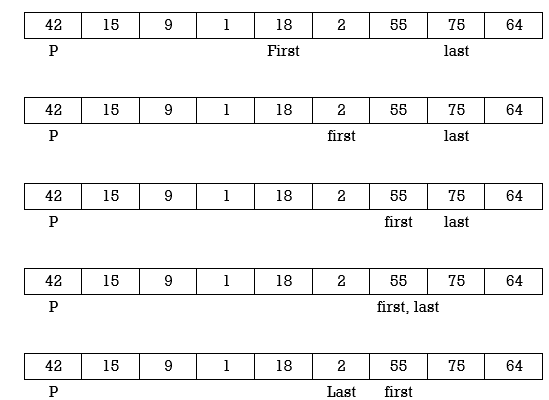
Swap p and A[last]
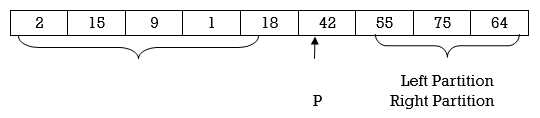
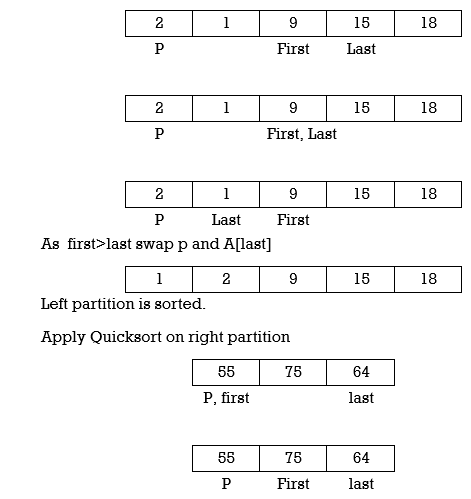
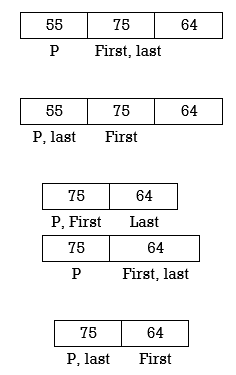
Applying Quick sort on left partition
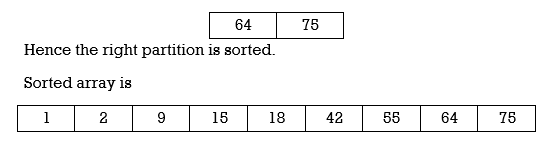
Program for Quick Sort:
#include<stdio.h>
void quicksort(int A[10],int,int);
int main()
{
int A[20],n,i;
printf("Enter size of the array: ");
scanf("%d",&n);
printf("Enter %d elements: ",n);
for(i=0;i<n;i++)
scanf("%d",&A[i]);
quicksort(A,0,n–1);
printf("Sorted elements: ");
for(i=0;i<n;i++)
printf(" %d",A[i]);
return 0;
}
void quicksort(int A[20],int first, int last)
{
int pivot,j,temp,i;
if(first<last){
pivot=first;
i=first;
j=last;
while(i<j){
while(A[i]<=A[pivot]&&i<last)
i++;
while(A[j]>A[pivot])
j––;
if(i<j){
temp=A[i];
A[i]=A[j];
A[j]=temp;
}
}
temp=A[pivot];
A[pivot]=A[j];
A[j]=temp;
quicksort(A,first,j–1);
quicksort(A,j+1,last);
}
}
Output:
Enter size of the array: 5
Enter 5 elements: 3 8 0 1 2
Sorted elements: 0 1 2 3 8
Complexity of Quick Sort
The time to sort the file is equal to
Q8) Describe worst case analysis?
A8) The pivot is the smallest element
T(N) = T (N – 1) + cN, N > 1
T (N – 1) =T (N – 2) + c (N – 1)
T (N – 2) =T (N – 3) + c (N – 2)
T (N – 3) =T (N – 4) + c (N– 3)
T (2) =T (1) + c.2
Add all equations:
T(N) + T (N – 1) + T (N – 2) + … + T (2) =
= T (N – 1) + T (N – 2) + … + T (2) + T (1) + c(N) + c (N – 1) + c (N – 2) + … + c.2
T(N) = T (1) + c times (the sum of 2 thru N) = T (1) + c(N(N+1)/2 –1) = O(N2)
Q9) Explain best case analysis?
A9) The pivot is in the middle
T(N)=2T(N/2) + cN
Divide by N:
T(N) / N=T(N/2) / (N/2) + c
T(N/2) / (N/2) =T(N/4) / (N/4) + c
T(N/4) / (N/4) =T(N/8) / (N/8) + c
…..
T (2) / 2=T (1) / (1) + c
Add all equations:
T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + …. + T (2) / 2
= (N/2) / (N/2) + T(N/4) / (N/4) + … + T (1) / (1) + c. logN
After crossing the equal terms:
T(N)/N=T (1) + cLogN
T(N)=N + NcLogN = O(NlogN)
Q10) Explain Average case analysis?
A10) Similar computations, resulting in T(N) = O(NlogN)
The average value of T(i) is 1/N times the sum of T (0) through T(N–1)
1/N S T(j), j = 0 thru N–1
T(N)=2/N (S T(j)) + cN
Multiply by N
NT(N) =2(S T(j)) + cN*N
To remove the summation, we rewrite the equation for N–1:
(N–1) T(N–1) =2(S T(j)) + c(N–1)2, j = 0 thru N–2
and subtract:
NT(N) – (N–1) T(N–1) =2T(N–1) + 2cN –c
NT(N) =(N+1) T(N–1) + 2cN
Divide by N(N+1):
T(N)/(N+1) =T(N–1)/N + 2c/(N+1)
T(N)/(N+1) =T(N–1)/N + 2c/(N+1)
T(N–1)/(N)=T(N–2)/(N–1) + 2c/(N)
T(N–2)/(N–1) =T(N–3)/(N–2) + 2c/(N–1)
….
T (2)/3 =T (1)/2 + 2c /3
Add the equations and cross equal terms:
T(N)/(N+1) =T (1)/2 +2c S (1/j), j = 3 to N+1
The sum S (1/j), j =3 to N–1, is about LogN
Thus T(N)=O(NlogN)
Q11) Define Merge sort? With example?
A11) Merge Sort is based on divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First, we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally, every sublist contains only one element.
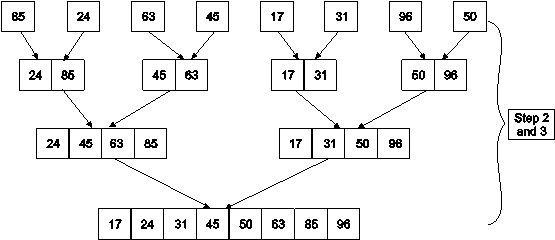
Step 2: Now we start from bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus, we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until entire list is sorted. Thus, above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
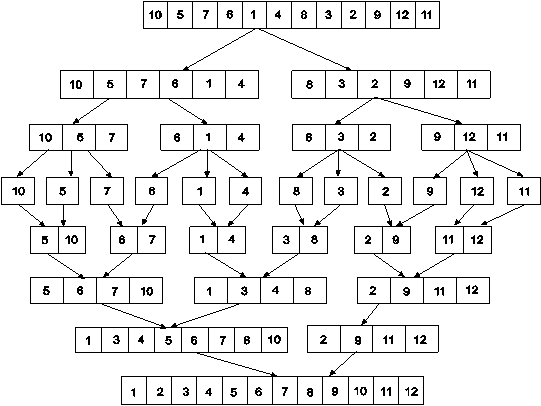
Example: Apply merge Sort on array A= {10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
Algorithm for Merge Sort:
Let x=no. of elements in array A
y=no. of elements in array B
C=sorted array with no. of elements n
n=x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA: = 1,
LB: = 1 and
LC: = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC: = LC + 1,
LA: = LA + 1, if new element has come from A.
LB: = LB + 1, if new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
 LB >y, then the remaining elements of A are assigned to C.
LB >y, then the remaining elements of A are assigned to C.
Thus, the algorithm becomes
MERGING (A, x, B, y, C)
1. [Initialize] Set LA: = 1, LB: = 1 AND LC: = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB], then
(a) [Assign element from A to C] set C[LC] = A[LA]
(b) [Update pointers] Set LC: = LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC: = LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x, then
Repeat for K= 0 ,1,2, ........, y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2, ......, x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Program for Merge Sort
#include<stdio.h>
#define MAX 50
void mergeSort(int A[],int first,int mid,int high);
void divide(int A[],int first,int last);
int main()
{
int merge[MAX],i,n;
printf("Enter the total number of elements: ");
scanf("%d",&n);
printf("Enter the elements which to be sort: ");
for(i=0;i<n;i++){
scanf("%d",&merge[i]);
}
divide(merge,0,n–1);
printf("After merge sorting elements are: ");
for(i=0;i<n;i++){
printf("%d ",merge[i]);
}
return 0;
}
void divide(int A[],int first, int last)
{
int mid;
if(first<last){
mid=(first+last)/2;
divide(A,first,mid);
divide(A,mid+1,last);
mergeSort(A,first,mid,last);
}
}
void mergeSort(int A[],int first,int mid,int last)
{
int i,m,k,l,temp[MAX];
l=first;
i=first;
m=mid+1;
while((l<=mid)&&(m<=last)){
if(A[l]<=A[m]){
temp[i]=A[l];
l++;
}
else{
temp[i]=A[m];
m++;
}
i++;
}
if(l>mid){
for(k=m;k<=last;k++){
temp[i]=arr[k];
i++;
}
}
else{
for(k=l;k<=mid;k++){
temp[i]=arr[k];
i++;
}
}
for(k=first;k<=last;k++){
A[k]=temp[k];
}
}
Output:
Enter the total number of elements: 5
Enter the elements which to be sort: 3 1 6 4 7
After merge sorting elements are: 1 3 4 6 7
Q12) Describe Complexity of Merge sort?
A12) Time to merge sort N elements = Time to merge sort N/2 elements plus time to merge two arrays each N/2 elements.
Time to merge two arrays each N/2 elements is linear, i.e., N
Thus, we have:
(1) T (1) = 1
(2) T(N) = 2T(N/2) + N
Dividing (2) by N we get:
(3) T(N) / N = T(N/2) / (N/2) + 1
N is a power of two, so we can write
(4) T(N/2) / (N/2) = T(N/4) / (N/4) +1
(5) T(N/4) / (N/4) = T(N/8) / (N/8) +1
(6) T(N/8) / (N/8) = T(N/16) / (N/16) +1
(7) ……
(8) T (2) / 2 = T (1) / 1 + 1
Adding equations (3) through (8), the sum of their left–hand sides will be equal to the sum of their right–hand sides:
T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + … + T (2)/2
= T(N/2) / (N/2) + T(N/4) / (N/4) + …. + T (2) / 2 + T (1) / 1 + LogN
(LogN is the sum of 1s in the right–hand sides)
After crossing the equal term, we get
(9) T(N)/N = T (1)/1 + LogN
T (1) is 1, hence we obtain
(10) T(N) = N + NlogN = O(NlogN)
Hence the complexity of the Merge Sort algorithm is O(NlogN).
Q13) What is Heap Sort? With example?
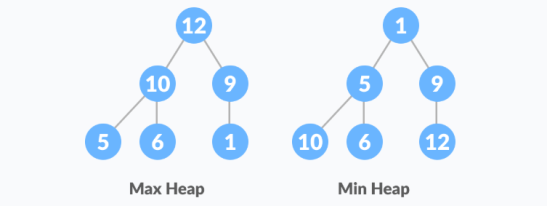
A13) Heap is a special tree-based data structure. A binary tree is said to follow a heap data structure if it is a complete binary tree
All nodes in the tree follow the property that they are greater than their children i.e., the largest element is at the root and both its children and smaller than the root and so on. Such a heap is called a max-heap. If instead, all nodes are smaller than their children, it is called a min-heap
The following example diagram shows Max-Heap and Min-Heap.
Starting from a complete binary tree, we can modify it to become a Max-Heap by running a function called heapify on all the non-leaf elements of the heap.
heapify(array)
Root = array [0]
Largest = largest (array [0], array [2*0 + 1]. array [2*0+2])
if (Root! = Largest)
Swap (Root, Largest)
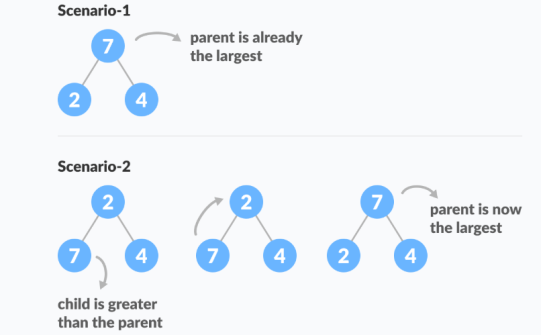
The example above shows two scenarios - one in which the root is the largest element and we don't need to do anything. And another in which the root had a larger element as a child and we needed to swap to maintain max-heap property
Q14) Explain in place / outplace technique?
A14) A sorting technique is in place if it does not use any extra memory to sort the array.
Among the comparison-based techniques discussed, only merge sort is outplaced technique as it requires an extra array to merge the sorted subarrays.
Among the non-comparison-based techniques discussed, all are outplaced techniques. Counting sort uses a counting array and bucket sort uses a hash table for sorting the array.
Q15) Explain online / offline technique?
A15) A sorting technique is considered Online if it can accept new data while the procedure is ongoing i.e., complete data is not required to start the sorting operation.
Among the comparison-based techniques discussed, only Insertion Sort qualifies for this because of the underlying algorithm it uses i.e., it processes the array (not just elements) from left to right and if new elements are added to the right, it doesn’t impact the ongoing operation.
Q16) Explain stable/ unstable technique?
A16) A sorting technique is stable if it does not change the order of elements with the same value.
Out of comparison-based techniques, bubble sort, insertion sort and merge sort are stable techniques. Selection sort is unstable as it may change the order of elements with the same value. For example, consider the array 4, 4, 1, 3.
In the first iteration, the minimum element found is 1 and it is swapped with 4 at 0th position. Therefore, the order of 4 with respect to 4 at the 1st position will change. Similarly, quick sort and heap sort are also unstable.
Q17) Define Hashing?
A17) Hashing is an important Data Structure which is designed to use a special function called the Hash function which is used to map a given value with a particular key for faster access of elements. The efficiency of mapping depends of the efficiency of the hash function used.
Let a hash function H(x) maps the value  at the index x%10 in an Array. For example, if the list of values is [11,12,13,14,15] it will be stored at positions {1,2,3,4,5} in the array or Hash table respectively.
at the index x%10 in an Array. For example, if the list of values is [11,12,13,14,15] it will be stored at positions {1,2,3,4,5} in the array or Hash table respectively.