Unit - 2

Small Signal Analysis of BJTs and FETs

Q1) In a CB IE= 2mA, IC=1.5mA. Calculate IB?

A1) IE =IB+IC

2= IB+1.5

IB=0.5mA

Q2) In a CB current amplification factor is 0.9. If emitter current is 1.2mA. Determine the value of base current?

A2) α = 0.9

IE =1.2mA

α = IC/ IE

IC = α IE =0.9 x 1.2 = 1.08mA

IE =IB+IC

1.2= IB+1.08

IB= 0.12mA

Q3) In a CB connection IC=1.0mA and IB= 0.02mA. Find the value of current amplification factor?

A3) IE =IB+IC =1+0.02 = 1.02mA

α = IC/ IE

α = 1.0/1.02 = 0.98

Q4) In a CB connection the emitter current is 0.98mA. If the emitter circuit is open the collector current becomes 40A. Find total collector current. α =0.92

A4) ICBO=40A

IC = α IE+ICBO

    = (0.92 x 0.98x10-3) + 40x10-6

IC =0.94mA

Q5) In a common base connection, α = 0.95. The voltage drops across 3 kΩ resistance which is connected in the collector is 2.5 V. Find the base current.

A5) IC = 2.5/3000 = 0.83mA

α = IC/ IE

IE = IC/α =0.83/0.95=0.87mA

IE =IB+IC

0.87 =IB+0.83

IB=0.04mA

Q6) Find the value of β if (i) α = 0.9 (ii) α = 0.98 (iii) α = 0.99.

A6) = α/1- α = 0.9/1-0.9 = 9

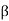= α/1- α = 0.98/1-0.98 = 49

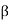= α/1- α = 0.99/1-0.99 = 99

Q7) The collector leakage current in a transistor is 200 μA in CE arrangement. If now the transistor is connected in CB arrangement, what will be the leakage current? Given that β = 120.

A7) ICEO=200 μA

= 120

α = /1+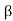= 120/121=0.99

ICEO=ICBO/1- α

ICBO= 1.6 μA

Q8) For a certain transistor, IB = 18 μA; IC = 2 mA and β = 60. Calculate ICBO.

A8)

IC = IB+ICEO

ICEO= IC - IB= 2x10-3-(60x18x10-6) = 0.92mA

α =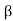 /1+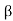= 60/61=0.98

ICBO= (1- α) ICEO = (1-0.98) x 0.92=15.08 μA

Q9) For T1  hie1 = 6 KΩ     hFe1 = 80       hre1 = hoe1 = 0

For T2  hie2 = 1 KΩ     hFe2 = 100     hre2 = hoe2 = 0

For the Darlington pair emitter follower, shown in figure, determine:

a)     Input impendence R1                      

b)    Voltage gain  VO / VS

c)     Current gain IO / IS

d)    Output impendence

A9) Given: hie1 = 6 KΩ     hFe1 = 80       hre1 = hoe1 = 0

hie2 = 1 KΩ     hFe2 = 100     hre2 = hoe2 = 0

Amplifier configuration:

Q1 → CC           Q2 → CC

Therefore, approximate analysis is used, for both stages

For second stage:

Current gain (Ai2)

AI2 = 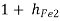= 1 + 100 = 101

Input resistance (Ri2)

RL1 = Ri2 = hie2 + (1 + hFe2) RL = 1 × 103 + (1 + 100) × 103 = 102 KΩ

Voltage gain (AV2):

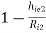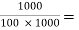AV2 = =1 - 0.99

For first stage:

Current gain (Ai1):

Ai1 = 1 + hFe1 = 81

Input resistance (Ri1):

Ri1 = hie1 + (1 + hFe1 )RL

      = 6 × 103 + (1 + 80) × 102 × 103 = 8.268 MΩ

Voltage gain (AV1):

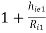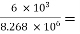AV1 = = 1 - 0.999

RO1 = 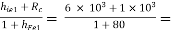86.42 Ω

RO2 =  10.76 Ω

Overall voltage gain (AV):

AV = AV1 × AV2 = 0.999 × 0.99 = 0.989

AVS

Figure shows equivalent circuit of the input side

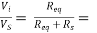0.998

AVS = 0.989 × 0.998 = 0.987

Overall voltage gain:

AI = Ai = Ai1 × Ai2 = 81 × 101 = 8181                      Ans.

Input impendence:

Ri = 0.89 MΩ                                                            Ans.

Overall voltage gain:

AV = 0.989                                                                 Ans.

Voltage gain include source:

AVS = 0.987                                                               Ans.

Output Impendence:

RO = 10.76 Ω                                                             Ans.

Q10) For the bootstrap circuit shown, calculate AI, Ri and AV. the transistor parameters are hie = 2 KΩ, hFe = 100, = 40 K and hre = 2.5 × 10-4.

A10) Given: hie = 2 KΩ, hFe = 100, = 40 K, hre = 2.5 × 10-4.

Amplifier configuration: common emitter with Re

AC analysis: For a.c. analysis of amplifier we consider the d.c. supply voltage as ground and capacitor as short circuit and apply Miller’s theorem across feedback resistor (10K) then modified circuit is given as:

The circuit down in fig. (a) represents a CE amplifier. But to analyse the bootstrapped element we need to consider the CC voltage gain first.

AV = common collector voltage gain

RL’ = 2K || 4K || 4K || 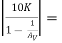1 K || 490 K = 1 KΩ

Assume AV 0.98

Checking approximation:

hoeRL’ 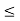0.1

0.025 < 0.1

Hence, valid approximation

Approximate analysis:

AI = 1 + hFe = 101

Ri = hie + (1 + hFe)RL’ = 2 + 101 = 103 KΩ             Ans.

AV = AI= 0.98

From fig. (a): R1  500 KΩ

Now, fig. (a) can be analysed by CE and the modified circuit is given as,

Checking approximation:

hoe (Re + RL) 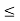0.1

Hence, valid approximation

Approximate analysis:

AI’= 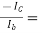-hFe = -100

Ri’= hie + (1 + hFe)Re’ = 2 + 101 × 1 = 103 KΩ

AV’ =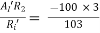

AV = AV’ = -2.9126

From fig. (b): Ri = Ri’ || 500K = 100 || 500 = 85.406 KΩ

AI =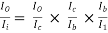

    = (-1) × 100 ×

From fig. (c): 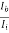- 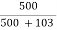= 0.8291

Hence, AI = - 100 × 0.82918 = -82.918

Q11) The bootstrapped Darlington pair uses identical transistors with the following h-parameters.

hie = 1 KΩ, hre = 2.5 × 10-4, hoe = 2.5 × 10-4 A/V, hFe = 100

Find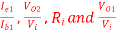

A11) Given: hie = 1 KΩ, hre = 2.5 × 10-4, hoe = 2.5 × 10-4 A/V, hFe = 100

Q1 – CC, Q2 - CC

For a.c. analysis of amplifier we consider the d.c. supply voltage as ground and capacitor as short circuit.

 Apply Miller’s theorem across R3 = (100K)

Voltage Gain:

AV = AV1 × AV2

Let us assume AV = 0.98

Where, = 4900 KΩ

RL’ = 0.1K || 82K || 10K || 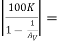0.1 K || 82 K || 10 K || 4900 K = 0.0988 KΩ

Analysis for Q2 [CC]:

Checking approximation:

hoeRL’ = 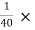0.0988 = 2.47 × 10-3 < 0.1

Approximate analysis:

AI2 = 1 + hFe = 101

Ri2 = hie + (1 + hFe)RL’ = 1 + 101 × 0.0988 = 10.9788 KΩ          

AV2 = AI2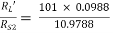= 0.908915

Analysis for Q1 [CC]:

RL = Ri2

hoeRL1 = 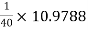= 0.27447 > 0.1

Exact analysis:

AI2 = 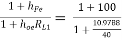= 79.2486

Ri1 = hie + AI1hrcRL1 = 1 + 79.2486 × 10.9788

         = 871.054 KΩ                     (hrc 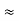1)

AV1 =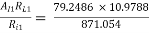

          = 0.99885

AV 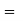AV1 × AV2 = 0.99885 × 0.908915

  = 0.9079                                      (Ans)

Ri = R || Ri1 = 1085.78 || 871.054                {Fig. (a)}

         = 483.32 KΩ

AI1 = 79.2486

AI =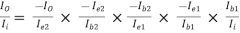

     =

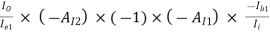
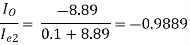
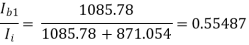
AI = (-0.9889) × (-101) × (-1) × (-79.2486) × 0.55487

    = 4391.94                                    (Ans)

Equation for VO/Vi:

Analysis of Q2 [CC]:

hoe(Re+RL)

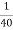× [0.0988 + 1] = 0.02747 < 0.1

Approximate analysis

AI2 = - hFe = -100

Ri2 = hie + (1 + hFe)Re

     = 1 +(1 + 100)0.0988 = 10.9788 KΩ

AV2 = 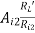= 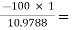-9.1084

Analysis of Q1 [CC]:

RL1 = Ri2 = 10.9788 KΩ

hoeRL1 = 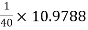 = 0.27447 > 0.1

Exact analysis:

AI1 = 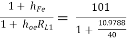= 79.2486

RL1 = hie + AI1RL1 = 1 + 79.2486 × 10.9788

     = 871.054 KΩ

AV1 = =

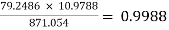
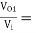AV = AV1 × AV2 = -9.0975

Hence, -AI1 = 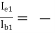79.248

Ri = 483.32 KΩ

-9.0975                                 (Ans)

Q12) A bootstrapped Darlington amplifier uses identical transistor with h-parameters, hie = 1.5 KΩ, hoe = 50 μA/V. If the circuit is to have Ri of 268 MΩ. Find the value of hFe for the transistor used.

A12) Given: hie = 1.5 KΩ, hoe = 50 μA/V, Ri = 2.68 MΩ, R1 = 1 MΩ, R2 = 1 MΩ, Re2 = 1 KΩ

RLeft = RC1 || RC2 = ∞ || 1 K = 1 KΩ

Amplifier configuration: bootstrapped Darlington pair amplifier [CC - CC]

Checking for approximation:

hoeRLeft 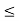0.1

hoeRLeft = 25 × 10-6 × 1 K = 0.025 < 0.1

which is less than 0.1

Approximate analysis:

Calculation for hFe

Ai2 = 1 + hFe

Ri2 = hie2 + Ai2RLeft = 1.5 K + (1 + hFe)1 K

Ai1= 1 + hFe

Ri1 = hie1 + Ai1RL1

Where RL1 = Ri2

Ri1 = 1.5K + (1 + hFe)[1.5K + (1 + hFe)1K]

2.68 MΩ = 1.5K + 1.5K + (1 + hFe)1K + 1.5Khfe + (1+hFe) 1KhFe

                 = 3K + 1K + 1KhFe + 1.5KhFe + 1KhFe + 1KhFe2

                 = 4K + 3.5KhFe + 1KhFe2

     = (4 + 3.5hFe + hFe2) × 103

hFe2 + 3.5hFe + 4 = 2680

hFe2 + 3.5hFe - 2676 = 0

The quadratic equation can be solved as,

hFe =

Substituting values we get,

hFe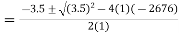

       = 50 or -53.5

hFe is always positive.

hFe = 50                                                          Ans.

Overall voltage gain:

(AV): AV = AV1 × AV2 = (1 - 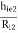)( 1 - )

                                   = (1 - )( 1 - )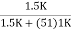

          = 0.999 × 0.971 = 0.97

Overall current gain –

Ai = Ai1 × Ai2

     = (1 + hFe) (1 + hFe)

     = (51)(51)

     = 26.01

Q13) For the circuit shown in figure assume that R1 = 30KΩ and R2 = 10 KΩ. Rd = 40KΩ. Vdd = 10V and VT=1V, Vgs = 2V and K = 0.1mA /V2. Find Id and VDS

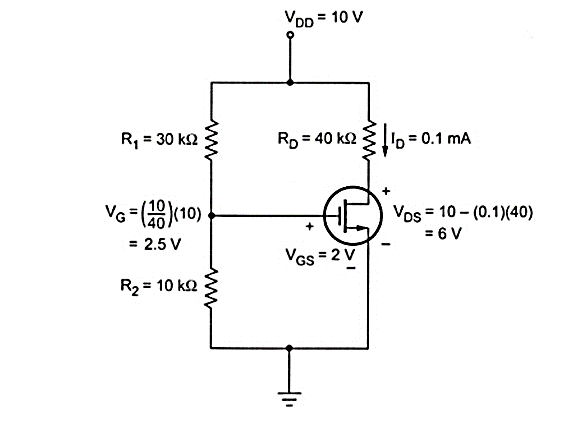
A13) VG = VGS = (R2/R1+R2) VDD = (10/10+30) (10) = 2.5V

Assuming that the MOSFET is biased in the saturation region the drain current is

VDS = VDD – ID RD = 10 – (0.1) (40) = 6V.

Here, the source is tied to +VDD, Which, become signal ground in the a.c. equivalent circuit. Thus, it is also a common-source circuit.

The d.c. analysis for this circuit is essentially the same as for the n-channel MOSFET circuit. The gate voltage is given by,

VG = (R2/R1 + R2) (VDD)

And the source to gate voltage is given by

VSG = VDD -VG

Assuming VGS <VT or VSG > |VT| the device in the saturation region and the drain current is given by

ID = K (VSG + VT) 2

And the source to drain voltage is given by

VSD = VDD – ID RD

If VSD > VSD (sat) then MOSFET is in saturation region.

IF VSD < VSD (sat) MOSFET is in non-saturation region.

Q14) For the circuit shown in figure calculate ID , VDS, VG and VS

A14) Applying KVL to the input circuit.

VGS = VG – VS

         = 3 – IS RS          Since VS = IS RS

        = 3 – ID RS          Since ID = IS

We have

ID = IDSS (1 – VGS / VP) 2

Substituting the value of VGS  we get

ID = IDSS (1 – (3 – ID RS)/Vp) 2 = 20 x 10 -3 (1 – (3 – ID x 1.2 x 10 3 / -6)

       = 20 x 10 -3 (1 – [ (-0.5) + 200 ID]) 2 = 20 x 10 -3 (1.5 -2)

       = 20 x 10 -3 (2.25 – 600ID + 40000ID 2)

I D = 0.045 – 12 I D + 800 I D 2

800 I D 2 – 13 I D + 0.045 =0

Solving for quadratic equation we get

= -(-13) ± [ (13) 2 – 4(800) (0.045)] ½ / 2(800)

= 13 ± [ 169 -144] ½ / 1600 = 13 ±   / 1600 = 13 ± 5 /1600 = 5mA or 11.25 mA

If we calculate the value of VDS taking ID = 11.25mA we get

VDS = VDD – ID (RD + RS)

        = 12 – 11.25 x 10 -3 (500 + 1.2 x 10 3)

        = 12 – 19.125 = -7.125

Practically the value of VDS must be positive hence ID= 11.25 mA is invalid

Hence take ID = 5mA

VDS = VDD – ID (RD + RS) = 12 – 5 x 10 -3 (500 + 1.2 x 10 3) = 12 – 8.5 = 3.5 V

VGS = 3 – ID RS = 3- 5 x 10 -3 x 1.2 x 10 3 = 3 – 6 = -3 V

Vs = ID RS   = 5 x 10 -3 x 1.2 x 10 3 = 6V

Q15) List characteristics of CB amplifier?

A15) Characteristics of Common Base Amplifier

(i)                Current gain is less than unity and its magnitude decreases, with the increase of load resistance RL

(ii)              Voltage gain AV is high for normal values of RL

(iii)           The input resistance Ri is the lowest of all the three configurations, and

(iv)            The output resistance Ro is the highest of all the three configurations.

Applications The CB amplifier is not commonly used for amplification purpose. It is used for

(i)                Matching a very low impedance source

(ii)              As a non-inverting amplifier to voltage gain exceeding unity.

(iii)           For driving a high impedance load. (iv)As a constant current source.

Q16) List the characteristics of CE amplifier?

A16) Characteristics of Common Emitter Amplifier

(i)                The current gain Ai is high for RL < 10 kΩ.

(ii)              The voltage gain is high for normal values of load resistance RL.

(iii)           The input resistance Ri is medium.

(iv)            The output resistance Ro is moderately high.

Applications: CE amplifier is widely used for amplification

Q17) Mention values of Av, Ai Re Ro for CE, CB and CC amplifier?

A17)