Unit - 2
Data representation
Q1) What do you mean by signed number representation?
A1) Signed Number Representation
Variables such as integers can be represented in two ways, i.e., signed and unsigned. Signed numbers use a sign flag or can distinguish between negative values and positive values. Whereas unsigned numbers stored only positive numbers but not negative numbers.
Number representation techniques like Binary, Octal, Decimal, and Hexadecimal number representation techniques can represent numbers in both signed and unsigned ways. Binary Number System is one type of Number Representation techniques. It is most popular and used in digital systems. The binary system is used for representing binary quantities which can be represented by any device that has only two operating states or possible conditions. For example, a switch has only two states: open or close.
In the Binary System, there are only two symbols or possible digit values, i.e., 0 and 1. Represented by any device that only has 2 operating states or possible conditions. Binary numbers are indicated by the addition of either an 0b prefix or a 2 suffix.
Representation of Binary Numbers:
Binary numbers can be represented in the signed and unsigned way. Unsigned binary numbers do not have a sign bit, whereas signed binary numbers use a signed bit as well or these can be distinguishable between positive and negative numbers. A signed binary is a specific data type of a signed variable.
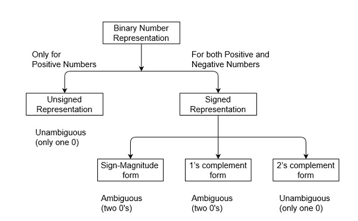
Fig 1 – Binary number representation
1. Unsigned Numbers:
Unsigned numbers don’t have any sign, these can contain the only magnitude of the number. So, the representation of unsigned binary numbers is all positive numbers only. For example, the representation of positive decimal numbers is positive by default. We always assume that there is a positive sign symbol in front of every number.
Representation of Unsigned Binary Numbers:
Since there is no sign bit in this unsigned binary number, so N bit binary number represents its magnitude only. Zero (0) is also an unsigned number. This representation has only one zero (0), which is always positive. Every number in unsigned number representation has only one unique binary equivalent form, so this is an unambiguous representation technique. The range of unsigned binary numbers is from 0 to (2n-1).
Example-1: Represent decimal number 92 in an unsigned binary number.
Simply convert it into a Binary number, it contains the only magnitude of the given number.
= (92)10
= (1x26+0x25+1x24+1x23+1x22+0x21+0x20)10
= (1011100)2
It’s 7-bit binary magnitude of the decimal number 92.
Example-2: Find a range of 5-bit unsigned binary numbers. Also, find the minimum and maximum values in this range.
Since the range of unsigned binary numbers is from 0 to (2n-1). Therefore, the range of 5-bit unsigned binary numbers is from 0 to (25-1) which is equal from minimum value 0 (i.e., 00000) to maximum value 31 (i.e., 11111).
2. Signed Numbers:
Signed numbers contain a sign flag, this representation distinguishes positive and negative numbers. This technique contains both the sign bit and magnitude of a number. For example, in the representation of negative decimal numbers, we need to put a negative symbol in front of a given decimal number.
Representation of Signed Binary Numbers:
There are three types of representations for signed binary numbers. Because of the extra signed bit, binary number zero has two representations, either positive (0) or negative (1), so ambiguous representation. But 2’s complementation representation is unambiguous because there is no double representation of number 0. These are Sign-Magnitude form, 1’s complement form, and 2’s complement form which are explained below.
2. (a) Sign-Magnitude form:
For n bit binary numbers, 1 bit is reserved for the sign symbol. If the value of the sign bit is 0, then the given number will be positive, else if the value of the sign bit is 1, then the given number will be negative. The Remaining (n-1) bits represent the magnitude of the number. Since the magnitude of number zero (0) is always 0, so there can be two representations of number zero (0), positive (+0), and negative (-0), depending on the value of the sign bit. Hence these representations are ambiguous generally because of two representations of number zero (0). Generally, the sign bit is the most significant bit (MSB) of representation. The range of Sign-Magnitude form is from (2(n-1)-1) to (2(n-1)-1).
For example, range of 6-bit Sign-Magnitude form binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i.e., 1 11111) to maximum value +31 (i.e., 0 11111). And zero (0) has two representations, -0 (i.e., 1 00000) and +0 (i.e., 0 00000).
2. (b) 1’s complement form:
Since 1’s complement of a number is obtained by inverting each bit of a given number. So, we represent positive numbers in binary form and negative numbers in 1’s complement form. There is an extra bit for sign representation. If the value of the sign bit is 0, then the number is positive and you can directly represent it in simple binary form, but if the value of the sign bit 1, the number is negative and you have to take 1’s complement of the given binary number. You can get the negative number by 1’s complement of a positive number and positive number by using 1’s complement of a negative number. Therefore, in this representation, zero (0) can have two representations, that’s why 1’s complement form is also ambiguous. The range of 1’s complement form is from (2(n-1)-1) to (2(n-1)-1).
For example, the range of 6 bit 1’s complement from the binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representations, -0 (i.e., 1 11111) and +0 (i.e., 0 00000).
2. (c) 2’s complement form:
Since 2’s complement of a number is obtained by inverting each bit of a given number plus 1 to the least significant bit (LSB). So, we represent positive numbers in binary form and negative numbers in 2’s complement form. There is an extra bit for sign representation. If the value of the sign bit is 0, then the number is positive and you can directly represent it in simple binary form, but if the value of the sign bit 1, the number is negative and you have to take 2’s complement of the given binary number. You can get the negative number by 2’s complement of a positive number and positive number by directly using simple binary representation. If the value of the most significant bit (MSB) is 1, then take 2’s complement form, else not. Therefore, in this representation, zero (0) has only one (unique) representation which is always positive. The range of 2’s complement form is from (2(n-1)) to (2(n-1)-1).
For example, the range of 6 bit 2’s complement form binary number is from (25) to (25-1) which is equal from minimum value -32 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representations, -0 (i.e., 1 11111) and +0 (i.e., 0 00000).
Q2) Explain fixed point representation?
A2) Fixed point representation
Digital Computers use a Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i.e., 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.
There are various types of number representation techniques for digital number representation, for example, Binary number system, octal number system, decimal number system, and hexadecimal number system, etc. But the Binary number system is most relevant and popular for representing numbers in the digital computer system.
Storing Real Number
These are structures as below −
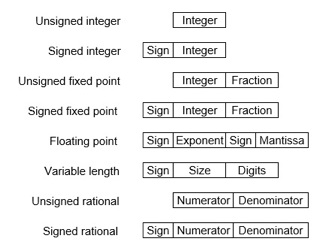
There are two major approaches to storing real numbers (i.e., numbers with fractional components) in modern computing. These are (i) Fixed-Point Notation and (ii) Floating Point Notation. In fixed-point notation, there is a fixed number of digits after the decimal point, whereas a floating-point number allows for a varying number of digits after the decimal point.
Fixed-Point Representation −
This representation has a fixed number of bits for the integer part and fractional part. For example, if a fixed-point representation is IIII. FFFF, then you can store the minimum value is 0000. 0001 and the maximum value is 9999. 9999. There are three parts of a fixed-point number representation: the sign field, integer field, and fractional field.
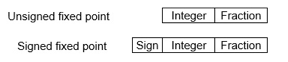
We can represent these numbers using:
● Signed representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
● 1’s complement representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
● 2’s complementation representation: range from -(2(k-1)) to (2(k-1)-1), for k bits.
2’s complementation representation is preferred in the computer system because of its unambiguous property and easier of arithmetic operations.
Example −Assume number is using a 32-bit format which reserves 1 bit for the sign, 15 bits for the integer part, and 16 bits for the fractional part.
Then, -43. 625 is represented as follows:

Where 0 is used to represent + and 1 is used to represent. 000000000101011 is a 15-bit binary value for decimal 43 and 1010000000000000 is a 16-bit binary value for fractional 0. 625.
The advantage of using a fixed-point representation is performance and the disadvantage is a relatively limited range of values that they can represent. So, it is usually inadequate for numerical analysis as it does not allow enough numbers and accuracy. A number whose representation exceeds 32 bits would have to be stored inexactly.
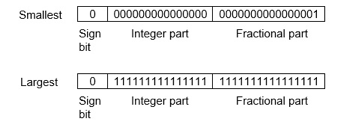
These are above the smallest positive number and largest positive number which can be stored in 32-bit representation as given above format. Therefore, the smallest positive number is 2-16 ≈ 0. 000015 approximate and the largest positive number is (215-1) +(1-2-16) =215(1-2-16) =32768, and the gap between these numbers is 2-16.
We can move the radix point either left or right with the help of only the integer field is 1.
Q3) What is floating point representation?
A3) Floating Point representation
This representation does not reserve a specific number of bits for the integer part or the fractional part. Instead, it reserves a certain number of bits for the number (called the mantissa or significand) and a certain number of bits to say where within that number the decimal place sits (called the exponent).
The floating number representation of a number has two-part: the first part represents a signed fixed-point number called the mantissa. The second part designates the position of the decimal (or binary) point and is called the exponent. The fixed-point mantissa may be a fraction of an integer. Floating -point is always interpreted to represent a number in the following form: Mxre.
Only the mantissa m and the exponent e are physically represented in the register (including their sign). A floating-point binary number is represented similarly except that it uses base 2 for the exponent. A floating-point number is said to be normalized if the most significant digit of the mantissa is 1.
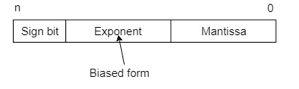
So, the actual number is (-1) s(1+m) x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number.
Note that signed integers and exponents are represented by either sign representation, or one’s complement representation, or two’s complement representation.
The floating-point representation is more flexible. Any non-zero number can be represented in the normalized form of ± (1. b1b2b3 . . . )2x2n This is the normalized form of a number x.
Example −Suppose the number is using the 32-bit format: the 1-bit sign bit, 8 bits for the signed exponent, and 23 bits for the fractional part. The leading bit 1 is not stored (as it is always 1 for a normalized number) and is referred to as a “hidden bit”.
Then −53.5 is normalized as -53.5= (-110101.1)2= (-1.101011) x25, which is represented as below,

Where 00000101 is the 8-bit binary value of exponent value +5.
Note that 8-bit exponent field is used to store integer exponents -126 ≤ n ≤ 127.
The smallest normalized positive number that fits into 32 bits is (1. 00000000000000000000000)2x2-126=2-126≈1.18x10-38 and the largest normalized positive number that fits into 32 bits is (1. 11111111111111111111111)2x2127= (224-1) x2104 ≈ 3.40x1038. These numbers are represented as below,

The precision of a floating-point format is the number of positions reserved for binary digits plus one (for the hidden bit). In the examples considered here, the precision is 23+1=24.
The gap between 1 and the next normalized floating-point number is known as machine epsilon. The gap is (1+2-23)-1=2-23for the above example, but this is the same as the smallest positive floating-point number because of non-uniform spacing unlike in the fixed-point scenario.
Note that non-terminating binary numbers can be represented in floating-point representation, e. g., 1/3 = (0. 010101 . . . )2 cannot be a floating-point number as its binary representation is non-terminating.
IEEE Floating point Number Representation −
IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation as the following diagram.
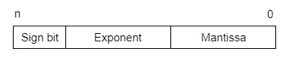
So, the actual number is (-1) s(1+m) x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number. The sign bit is 0 for a positive number and 1 for a negative number. Exponents are represented by or two’s complement representation.
According to IEEE 754 standard, the floating-point number is represented in the following ways:
● Half Precision (16 bit): 1 sign bit, 5-bit exponent, and 10-bit mantissa
● Single Precision (32 bit): 1 sign bit, 8-bit exponent, and 23-bit mantissa
● Double Precision (64 bit): 1 sign bit, 11-bit exponent, and 52-bit mantissa
● Quadruple Precision (128 bit): 1 sign bit, 15-bit exponent, and 112-bit mantissa
Special Value Representation −
Some special values depended upon different values of the exponent and mantissa in the IEEE 754 standard.
● All the exponent bits 0 with all mantissa bits 0 represents 0. If the sign bit is 0, then +0, else -0.
● All the exponent bits 1 with all mantissa bits 0 represents infinity. If the sign bit is 0, then +∞, else -∞.
● All the exponent bits 0 and mantissa bits non-zero represent a denormalized number.
● All the exponent bits 1 and mantissa bits non-zero represent error.
Q4) Define character representation?
A4) Character Representation
Everything represented by a computer is represented by binary sequences.
A common non-integer to be represented is a character. We use standard encodings (binary sequences) to represent characters.
REMEMBER: bit patterns do NOT imply a representation
A 4-bit binary quantity is called a nibble. An 8-bit binary quantity is called a byte.
Many I/O devices work with 8-bit quantities. A standard code ASCII (American Standard for Computer Information Interchange) defines what character is represented by each sequence. You'll look these up in an ASCII table.
Examples:
0100 0001 is 41 (hex) or 65 (decimal). It represents 'A'
0100 0010 is 42 (hex) or 66 (decimal). It represents 'B'
Different bit patterns are used for each different character that needs to be represented.
The code has some nice properties. If the bit patterns are compared, (pretending they represent integers), then 'A' < 'B'. This is good because it helps with sorting things into alphabetical order.
Notes:
● 'a' (0x61) is different than 'A' (0x41)
● '8' (0x38) is different than the integer 8
two's complement representation for 8: 0000 0000 0000 0000 0000 0000 0000 1000
the ASCII character '8': 0011 1000
● the digits:
'0' is 48 (decimal) or 0x30
'9' is 57 (decimal) or 0x39
Because of this difference between the integer representation for a character, and the character representation for a character, we constantly need to convert from one to the other.
The computer does arithmetic operations on two's complement integers (and often operations on unsigned integers). The computer can read in or print out a single character representation at a time. So, any time we want to do I/O, we're working with one character at a time and the ASCII representation of the character. Yet, lots of the time, the data represents numbers (just consider integers, for now).
Characters that represent an integer
To read in an integer, and then process the integer, consider an example. Suppose the user types the 4-character sequence 123\n.
The computer can read in a single character at a time. If it reads in exactly 4 characters, then the representations that the computer will have will be
ASCII decimal binary integer 8-bit two's comp.
character hex value desired representation
'1' 0x31 49 00110001 1 00000001
'2' 0x32 50 00110010 2 00000010
'3' 0x33 51 00110011 3 00000011
'\n' 0x0a 10 00001010 (NA) (NA)
From this example, it should be easy to see that conversion of a single ASCII character representation to the desired two's complement integer representation does an integer subtraction.
integer rep desired = ASCII representation - 48
What we need is an algorithm for translating multi-character strings to the integers they represent and vice versa.
ALGORITHM: character string --> integer
the steps:
for '3' '5' '4'
integer = 0
read '3'
translate '3' to 3
integer = integer * 10 + 3 = 3
read '5'
translate '5' to 5
integer = integer * 10 + 5 = 35
read '4'
translate '4' to 4
integer = integer * 10 + 4 = 354
the algorithm:
integer = 0
while there are more characters
get character
digit <- character - 48
integer <- integer * 10 + digit
Going the other direction for translation (integer to set of characters represented, printed out in the correct order), we partially reverse the algorithm.
ALGORITHM: integer --> character string
the steps:
For 354, figure out how many characters there are in
the base desired (3).
Figure out base^ (number of characters - 1) (10^2) =100
354 div 100 gives 3
translate 3 to '3' and print it out
354 % 100 gives 54
100/10 = 10
54 div 10 gives 5
translate 5 to '5' and print it out
54 mod 10 gives 4
10/10 = 1
4 div 1 gives 4
translate 4 to '4' and print it out
4 mod 1 gives 0
1/10 = 0, so you're done
written in a form using two loops:
# figure out base^ (number of characters - 1)
power_of_base = base
while power_of_base is not large enough
power_of_base = power_of_base * base
while power_of_base! = 0
digit = integer / power_of_base
char_to_print = digit + 48
print char_to_print
integer = integer % power_of_base # remainder after integer division
power_of_base = power_of_base / base # quotient
Q5) What is Computer arithmetic – Integer addition and subtraction?
A5) Computer arithmetic – Integer addition and subtraction
Operations we'll get to know:
addition
subtraction
multiplication
division
logical operations (not, and, or, nand, nor, xor, xnor)
shifting
the rules for doing the arithmetic operations vary depending
on what representation is implied.
A LITTLE BIT ON ADDING
----------------------
an overview.
carry in a b | sum carry out
---------------+----------------
0 0 0 | 0 0
0 0 1 | 1 0
0 1 0 | 1 0
0 1 1 | 0 1
1 0 0 | 1 0
1 0 1 | 0 1
1 1 0 | 0 1
1 1 1 | 1 1
|
a 0011
+b +0001
-- -----
sum 0100
it's just like we do for decimals!
0 + 0 = 0
1 + 0 = 1
1 + 1 = 2 which is 10 in binary, sum is 0 and carries the 1.
1 + 1 + 1 = 3 sum is 1, and carries a 1.
ADDITION
--------
unsigned:
just like the simple addition given.
examples:
100001 00001010 (10)
+011101 +00001110 (14)
------- ---------
111110 00011000 (24)
ignore (throw away) carry out of the msb.
Why? Because computers ALWAYS work with fixed precision.
sign-magnitude:
rules:
- add magnitudes only (do not carry into the sign bit)
- throw away any carry out of the msb of the magnitude
(Due, again, to the fixed precision constraints.)
- add only integers of like sign (+ to + or - to -)
- sign of the result is the same as the sign of the addends
examples:
0 0101 (5) 1 1010 (-10)
+ 0 0011 (3) + 1 0011 (-3)
--------- ---------
0 1000 (8) 1 1101 (-13)
0 01011 (11)
+ 1 01110 (-14)
----------------
don't add! must do subtraction!
one's complement:
by example
00111 (7) 111110 (-1) 11110 (-1)
+ 00101 (5) + 000010 (2) + 11100 (-3)
----------- ------------ ------------
01100 (12) 1 000000 (0) wrong! 1 11010 (-5) wrong!
+ 1 + 1
---------- ----------
000001 (1) right! 11011 (-4) right!
so, it seems that if there is a carry out (of 1) from the msb, then the result will be off by 1, so add 1 again to get the correct result. (Implementation in HW called an "end around carry.")
two's complement:
rules:
- just add all the bits
- throw away any carry out of the msb
- (same as for unsigned!)
examples
00011 (3) 101000 111111 (-1)
+ 11100 (-4) + 010000 + 001000 (8)
------------ -------- --------
11111 (-1) 111000 1 000111 (7)
after seeing examples for all these representations, you may see why 2's complement addition requires simpler hardware than sign mag. or one's complement addition.
SUBTRACTION
-----------
general rules:
1 - 1 = 0
0 - 0 = 0
1 - 0 = 1
10 - 1 = 1
0 - 1 = borrow!
unsigned:
- it only makes sense to subtract a smaller number from a larger one
examples
1011 (11) must borrow
- 0111 (7)
------------
0100 (4)
sign-magnitude:
- if the signs are the same, then do subtraction
- if signs are different, then change the problem to addition
- compare magnitudes, then subtract smaller from larger
- if the order is switched, then switch the sign too.
- when the integers are of the opposite sign, then do
a - b becomes a + (-b)
a + b becomes a - (-b)
examples
0 00111 (7) 1 11000 (-24)
- 0 11000 (24) - 1 00010 (-2)
-------------- --------------
1 10110 (-22)
do 0 11000 (24)
- 0 00111 (7)
--------------
1 10001 (-17)
(Switch sign since the order of the subtraction was reversed)
one's complement:
figure it out on your own
two's complement:
- change the problem to addition!
a - b becomes a + (-b)
- so, get the additive inverse of b, and do addition.
Examples
10110 (-10)
- 00011 (3) --> 00011
------------ |
\|/
11100
+ 1
-------
11101 (-3)
so, do
10110 (-10)
+ 11101 (-3)
------------
1 10011 (-13)
(Throw away carry out)
OVERFLOW DETECTION IN ADDITION
unsigned -- when there is a carry out of the msb
1000 (8)
+1001 (9)
-----
1 0001 (1)
sign-magnitude -- when there is a carry out of the msb of the magnitude
1 1000 (-8)
+ 1 1001 (-9)
-----
1 0001 (-1) (carry out of msb of magnitude)
2's complement -- when the signs of the addends are the same, and the
sign of the result is different
0011 (3)
+ 0110 (6)
----------
1001 (-7) (note that a correct answer would be 9, but
9 cannot be represented in 4-bit 2's complement)
a detail -- you will never get overflow when adding 2 numbers of
opposite signs
OVERFLOW DETECTION IN SUBTRACTION
unsigned -- never
sign-magnitude -- never happen when doing subtraction
2's complement -- we never do subtraction, so use the addition rule
on the addition operation done.
MULTIPLICATION of integers
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
-- longhand, it looks just like decimal
-- the result can require 2x as many bits as the larger multiplicand
-- in 2's complement, to always get the right answer without
thinking about the problem, sign extend both multiplicands to
2x as many bits (as the larger). Then take the correct number
of result bits from the least significant portion of the result.
2's complement example:
1111 1111 -1
x 1111 1001 x -7
---------------- ------
11111111 7
00000000
00000000
11111111
11111111
11111111
11111111
+ 11111111
----------------
1 00000000111
-------- (correct answer underlined)
0011 (3) 0000 0011 (3)
x 1011 (-5) x 1111 1011 (-5)
------ -----------
0011 00000011
0011 00000011
0000 00000000
+ 0011 00000011
--------- 00000011
0100001 00000011
not -15 in any 00000011
representation! + 00000011
------------------
1011110001
take the least significant 8 bits 11110001 = -15
DIVISION of integers
unsigned only!
example of 15 / 3 1111 / 011
To do this longhand, use the same algorithm as for decimal integers.
LOGICAL OPERATIONS
done bitwise
X = 0011
Y = 1010
X AND Y is 0010
X OR Y is 1011
X NOR Y is 0100
X XOR Y is 1001
etc.
SHIFT OPERATIONS
a way of moving bits around within a word
3 types: logical, arithmetic and rotate
(Each type can go either left or right)
logical left - move bits to the left, same order
- throw away the bit that pops off the msb
- introduce a 0 into the lsb
00110101
01101010 (logically left shifted by 1 bit)
logical right - move bits to the right, same order
- throw away the bit that pops off the lsb
- introduce a 0 into the msb
00110101
00011010 (logically right-shifted by 1 bit)
arithmetic left - move bits to the left, same order
- throw away the bit that pops off the msb
- introduce a 0 into the lsb
- SAME AS LOGICAL LEFT SHIFT!
arithmetic right - move bits to the right, same order
- throw away the bit that pops off the lsb
- reproduce the original msb into the new msb
- another way of thinking about it: shift the
bits, and then do sign extension
00110101 -> 00011010 (arithmetically right-shifted by 1 bit)
1100 -> 1110 (arithmetically right-shifted by 1 bit)
rotate left - move bits to the left, same order
- put the bit that pops off the msb into the lsb,
so, no bits are thrown away or lost.
00110101 -> 01101010 (rotated left by 1 place)
1100 -> 1001 (rotated left by 1 place)
rotate right - move bits to the right, same order
- put the bit that pops off the lsb into the msb,
so, no bits are thrown away or lost.
00110101 -> 10011010 (rotated right by 1 place)
1100 -> 0110 (rotated right by 1 place)
Q6) Write about ripple carry adder?
A6) Ripple Carry Adder
● Ripple Carry Adder is a combinational logic circuit.
● It is used to add two n-bit binary numbers.
● It requires n full adders in its circuit for adding two n-bit binary numbers.
● It is also known as an n-bit parallel adder.
4-bit Ripple Carry Adder-
a 4-bit ripple carry adder is used to add two 4-bit binary numbers.
In Mathematics, any two 4-bit binary numbers A3A2A1A0 and B3B2B1B0 are added as shown below-
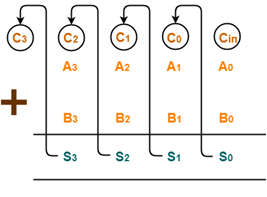
Fig 2 – Adding two 4-bit numbers
Using ripple carry adder, this addition is carried out as shown by the following logic diagram-
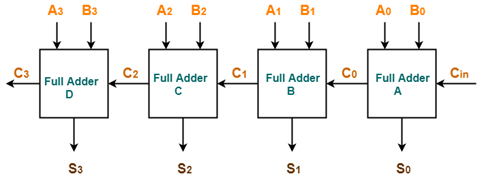
Fig 3 – 4-bit Ripple carry Adder
As shown-
● Ripple Carry Adder works in different stages.
● Each full adder takes the carry-in as input and produces carry-out and sum bit as output.
● The carry-out produced by a full adder serves as carry-in for its adjacent most significant full adder.
● When carry-in becomes available to the full adder, it activates the full adder.
● After the full adder becomes activated, it comes into operation.
Working of 4-bit Ripple Carry Adder-
Let-
● The two 4-bit numbers are 0101 (A3A2A1A0) and 1010 (B3B2B1B0).
● These numbers are to be added using a 4-bit ripple carry adder.
4-bit Ripple Carry Adder carries out the addition as explained in the following stages-
Stage-01:
● When Cin is fed as input to the full Adder A, it activates the full adder A.
● Then at full adder A, A0 = 1, B0 = 0, Cin = 0.
Full adder A computes the sum bit and carries bit as-
Calculation of S0–
S0 = A0 ⊕ B0 ⊕ Cin
S0 = 1 ⊕ 0 ⊕ 0
S0 = 1
Calculation of C0–
C0 = A0B0 ⊕ B0Cin ⊕ CinA0
C0 = 1. 0 ⊕ 0. 0 ⊕ 0. 1
C0 = 0 ⊕ 0 ⊕ 0
C0 = 0
Stage-02:
● When C0 is fed as input to the full adder B, it activates the full adder B.
● Then at full adder B, A1 = 0, B1 = 1, C0 = 0.
Full adder B computes the sum bit and carry bit as-
Calculation of S1–
S1 = A1 ⊕ B1 ⊕ C0
S1 = 0 ⊕ 1 ⊕ 0
S1 = 1
Calculation of C1–
C1 = A1B1 ⊕ B1C0 ⊕ C0A1
C1 = 0. 1 ⊕ 1. 0 ⊕ 0. 0
C1 = 0 ⊕ 0 ⊕ 0
C1 = 0
Stage-03:
● When C1 is fed as input to the full adder C, it activates the full adder C.
● Then at full adder C, A2 = 1, B2 = 0, C1 = 0.
Full adder C computes the sum bit and carry bit as-
Calculation of S2–
S2 = A2 ⊕ B2 ⊕ C1
S2 = 1 ⊕ 0 ⊕ 0
S2 = 1
Calculation of C2–
C2 = A2B2 ⊕ B2C1 ⊕ C1A2
C2 = 1. 0 ⊕ 0. 0 ⊕ 0. 1
C2 = 0 ⊕ 0 ⊕ 0
C2 = 0
Stage-04:
● When C2 is fed as input to the full adder D, it activates the full adder D.
● Then at full adder D, A3 = 0, B3 = 1, C2 = 0.
Full adder D computes the sum bit and carry bit as-
Calculation of S3–
S3 = A3 ⊕ B3 ⊕ C2
S3 = 0 ⊕ 1 ⊕ 0
S3 = 1
Calculation of C3–
C3 = A3B3 ⊕ B3C2 ⊕ C2A3
C3 = 0. 1 ⊕ 1. 0 ⊕ 0. 0
C3 = 0 ⊕ 0 ⊕ 0
C3 = 0
Thus finally,
● Output Sum = S3S2S1S0 = 1111
● Output Carry = C3 = 0
Why is the Ripple Carry Adder Called So?
In Ripple Carry Adder,
● The carry out produced by each full adder serves as carry-in for its adjacent most significant full adder.
● Each carries bit ripples or waves into the next stage.
● That’s why it is called “Ripple Carry Adder”.
Q7) Write the disadvantages of ripple carry adder?
A7) Disadvantages of Ripple Carry Adder-
● Ripple Carry Adder does not allow using all the full adders simultaneously.
● Each full adder has to necessarily wait until the carry bit becomes available from its adjacent full adder.
● This increases the propagation time.
● Due to this reason, the ripple carry adder becomes extremely slow.
● This is considered to be the biggest disadvantage of using a ripple carry adder.
Q8) Explain carry look-ahead adder?
A8) Carry look-ahead adder
In the case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called a ripple carry type adder.
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So, there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, the signal must propagate through the gates before the correct output sum is available in the output terminals.
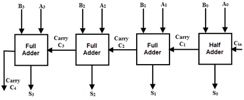
Fig 4 - Example
Consider the above figure, in which the sum S4 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input C4 is not available at its final steady-state value until carry c3 is available at its steady-state value. Similarly, C3 depends on C2 and C2 on C1. Therefore, carry must propagate to all the stages so that output S4 and carry C5 settle their final steady-state value.
The propagation time is equal to the propagation delay of the typical gate times the number of gate levels in the circuit. For example, if each full adder stage has a propagation delay of 20n seconds, then S4 will reach its final correct value after 80n (20 × 4) seconds. If we extend the number of stages for adding more bits then this situation becomes much worse.
So, the speed at which the number of bits added in the parallel adder depends on the carry propagation time. However, signals must be propagated through the gates at a given enough time to produce the correct or desired output.
The following are the methods to get the high speed in the parallel adder to produce the binary addition.
Carry-Lookahead Adder
A carry-Lookahead adder is a fast parallel adder as it reduces the propagation delay by more complex hardware, hence it is costlier. In this design, the carry logic over fixed groups of bits of the adder is reduced to two-level logic, which is nothing but a transformation of the ripple carry design.
This method makes use of logic gates to look at the lower order bits of the augend and add to see whether a higher-order carry is to be generated or not. Let us discuss this in detail.
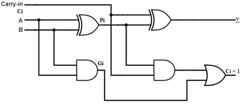
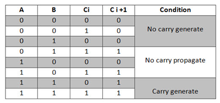
Fig 5 - Example
Consider the full adder circuit shown above with the corresponding truth table. If we define two variables as carry generate Gi and carry propagate Pi then,
Pi = Ai ⊕ Bi
Gi = Ai Bi
The sum output and carry output can be expressed as
Si = Pi ⊕ Ci
C i +1 = Gi + Pi Ci
Where Gi is a carry generator which produces the carry when both Ai, Bi are one regardless of the input carry. Pi is a carry propagate and it is associated with the propagation of carrying from Ci to Ci +1.
The carry output Boolean function of each stage in a 4-stage carry-Lookahead adder can be expressed as
C1 = G0 + P0 Cin
C2 = G1 + P1 C1
= G1 + P1 G0 + P1 P0 Cin
C3 = G2 + P2 C2
= G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin
C4 = G3 + P3 C3
= G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin
From the above Boolean equations, we can observe that C4 does not have to wait for C3 and C2 to propagate but C4 is propagated at the same time as C3 and C2. Since the Boolean expression for each carry output is the sum of products, these can be implemented with one level of AND gates followed by an OR gate.
The implementation of three Boolean functions for each carry output (C2, C3, and C4) for a carry-Lookahead carry generator is shown in the below figure.
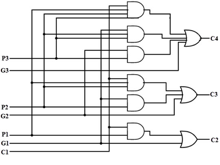
Fig 6 – Look ahead carry generator
Therefore, a 4-bit parallel adder can be implemented with the carry-Lookahead scheme to increase the speed of binary addition as shown in the figure below. In this, two Ex-OR gates are required by each sum output. The first Ex-OR gate generates Pi variable output and the AND gate generates the Gi variable.
Hence, in two gates levels, all these P’s and G’s are generated. The carry-Lookahead generators allow all these P and G signals to propagate after they settle into their steady-state values and produce the output carriers at a delay of two levels of gates. Therefore, the sum outputs S2 to S4 have equal propagation delay times.
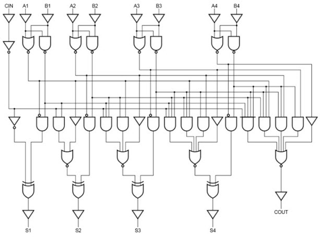
Fig 7 – example
It is also possible to construct 16 bit and 32-bit parallel adders by cascading the number of 4-bit adders with carry logic. A 16-bit carry-Lookahead adder is constructed by cascading the four 4-bit adders with two more gate delays, whereas the 32-bit carry-Lookahead adder is formed by cascading two 16-bit adders.
In a 16-bit carry-Lookahead adder, 5 and 8 gate delays are required to get C16 and S15 respectively, which are less as compared to the 9 and 10 gate delays for C16 and S15 respectively in cascaded four-bit carry-Lookahead adder blocks. Similarly, in 32-bit adders, 7 and 10 gate delays are required by C32 and S31 which are less compared to 18 and 17 gate delays for the same outputs if the 32-bit adder is implemented by eight 4-bit adders.
Carry-Lookahead Adder ICS
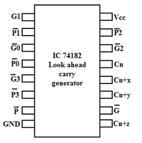
The high-speed carry-Lookahead adders are integrated on integrated circuits in different bit configurations by several manufacturers. There are several individual carry generator ICs available so that we have to make the connection with logic gates to perform the addition operation.
A typical carry-Lookahead generator IC is 74182 which accepts four pairs of active low carry propagate (as P0, P1, P2, and P3) and carry generate (Go, G1, G2, and G3) signals and an active high input (Cn).
It provides active high carriers (Cn+x, Cn+y, Cn+z) across the four groups of binary adders. This IC also facilitates the other levels of look-ahead by active low propagate and carry generate outputs.
The logic expressions provided by the IC 74182 are
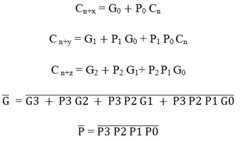
On the other hand, there are many high-speed adder ICs that combine a set of full adders with carry-Lookahead circuitry. The most popular form of such IC is 74LS83/74S283 which is a 4-bit parallel adder high-speed IC that contains four interconnected full adders with a carry-Lookahead circuitry.
The functional symbol for this type of IC is shown below figure. It accepts the two 4-bit numbers as A3A2A1A0 and B3B2B1B0 and input carry Cin0 into the LSB position. This IC produces output sum bits as S3S2S1S0 and the carry output Cout3 into the MSB position.
By cascading two or more parallel adder ICs we can perform the addition of larger binary numbers such as 8 bit, 24-bit, and 32-bit addition.
Q9) Describe Multiplication–shift and Add, Booth multiplier, Carry save multiplier?
A9) Multiplication–shift and Add, Booth multiplier, Carry save multiplier
Booth algorithm gives a procedure for multiplying binary integers in signed 2’s complement representation in the efficient way, i.e., less number of additions/subtractions required. It operates on the fact that strings of 0’s in the multiplier require no addition but just shifting and a string of 1’s in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^ (k+1) to 2^m.
As in all multiplication schemes, the booth algorithm requires examination of the multiplier bits and shifting of the partial product. Before the shifting, the multiplicand may be added to the partial product, subtracted from the partial product, or left unchanged according to the following rules:
Hardware Implementation of Booth's Algorithm – The hardware implementation of the booth algorithm requires the register configuration shown in the figure below.
Booth’s Algorithm Flowchart –
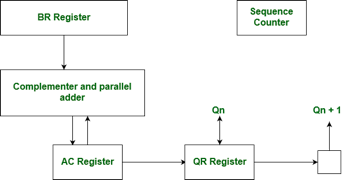
Fig 8 – Booth’s flowchart
We name the register as A, B, and Q, AC, BR, and QR respectively. Qn designates the least significant bit of multiplier in the register QR. An extra flip-flop Qn+1is appended to QR to facilitate a double inspection of the multiplier. The flowchart for the booth algorithm is shown below.
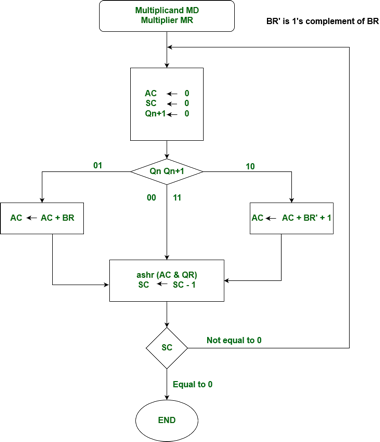
Fig 9 – Booth’s algorithm
AC and the appended bit Qn+1 are initially cleared to 0 and the sequence SC is set to a number n equal to the number of bits in the multiplier. The two bits of the multiplier in Qn and Qn+1are inspected. If the two bits are equal to 10, it means that the first 1 in a string has been encountered. This requires subtraction of the multiplicand from the partial product in AC. If the 2 bits are equal to 01, it means that the first 0 in a string of 0’s has been encountered. This requires the addition of the multiplicand to the partial product in AC.
When the two bits are equal, the partial product does not change. An overflow cannot occur because the addition and subtraction of the multiplicand follow each other. As a consequence, the 2 numbers that are added always have opposite signs, a condition that excludes an overflow. The next step is to shift right the partial product and the multiplier (including Qn+1). This is an arithmetic shift right (ashr) operation in which AC and QR to the right and leaves the sign bit in AC unchanged. The sequence counter is decremented and the computational loop is repeated n times.
Example – A numerical example of the booth’s algorithm is shown below for n = 4. It shows the step-by-step multiplication of -5 and -7.
MD = -5 = 1011, MD = 1011, MD'+1 = 0101
MR = -7 = 1001
The explanation of the first step is as follows: Qn+1
AC = 0000, MR = 1001, Qn+1 = 0, SC = 4
Qn Qn+1 = 10
So, we do AC + (MD)'+1, which gives AC = 0101
On right shifting AC and MR, we get
AC = 0010, MR = 1100 and Qn+1 = 1
OPERATION | AC | MR | Qn+1 | SC |
| 0000 | 1001 | 0 | 4 |
AC + MD’ + 1 | 0101 | 1001 | 0 |
|
ASHR | 0010 | 1100 | 1 | 3 |
AC + MR | 1101 | 1100 | 1 |
|
ASHR | 1110 | 1110 | 0 | 2 |
ASHR | 1111 | 0111 | 0 | 1 |
AC + MD’ + 1 | 0010 | 0011 | 1 | 0 |
The product is calculated as follows:
Product = AC MR
Product = 0010 0011 = 35
Best Case and Worst-Case Occurrence:
Best case is when there is a large block of consecutive 1’s and 0’s in the multipliers so that there is a minimum number of logical operations taking place, as in addition and subtraction.
The worst case is when there are pairs of alternate 0’s and 1’s, either 01 or 10 in the multipliers, so that maximum number of additions and subtractions are required.
Q10) Define Division restoring and non-restoring techniques?
A10) Division restoring and non-restoring techniques, floating point arithmetic
In an earlier post Restoring Division learned about restoring division. Now, here perform Non-Restoring division, it is less complex than the restoring one because the simpler operation is involved i.e., addition, and subtraction, also now restoring step is performed. In the method, rely on the sign bit of the register which initially contains zero named as A.
Let’s pick the step involved:
● Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
● Step-2: Check the sign bit of register A
● Step-3: If it is 1 shift left the content of AQ and perform A = A+M, otherwise shift left AQ and perform A = A-M (means add 2’s complement of M to A and store it to A)
● Step-4: Again, the sign bit of register A
● Step-5: If the sign bit is 1 Q [0] become 0 otherwise Q [0] become 1 (Q [0] means the least significant bit of register Q)
● Step-6: Decrement’s value of N by 1
● Step-7: If N is not equal to zero go to Step 2 otherwise go to the next step
● Step-8: If sign bit of A is 1 then perform A = A+M
● Step-9: Register Q contain quotient and A contain remainder
Examples: Perform Non_Restoring Division for Unsigned Integer
Dividend =11
Divisor =3
-M =11101
N | M | A | Q | Action |
4 | 00011 | 00000 | 1011 | Start |
|
| 00001 | 011_ | Left shift AQ |
|
| 11110 | 011_ | A=A-M |
3 |
| 11110 | 0110 | Q [0] =0 |
|
| 11100 | 110_ | Left shift AQ |
|
| 11111 | 110_ | A=A+M |
2 |
| 11111 | 1100 | Q [0] =0 |
|
| 11111 | 100_ | Left Shift AQ |
|
| 00010 | 100_ | A=A+M |
1 |
| 00010 | 1001 | Q [0] =1 |
|
| 00101 | 001_ | Left Shift AQ |
|
| 00010 | 001_ | A=A-M |
0 |
| 00010 | 0011 | Q [0] =1 |
Quotient = 3 (Q)
Remainder = 2 (A)
Restoring Division Algorithm for Unsigned Integer
A division algorithm provides a quotient and a remainder when we divide two numbers. They are generally of two types slow algorithm and fast algorithm. Slow division algorithms are restoring, non-restoring, non-performing restoring, SRT algorithm, and under fast comes Newton–Raphson, and Goldschmidt.
In this article, will be performing a restoring algorithm for an unsigned integer. Restoring term is due to the fact that the value of register A is restored after each iteration.
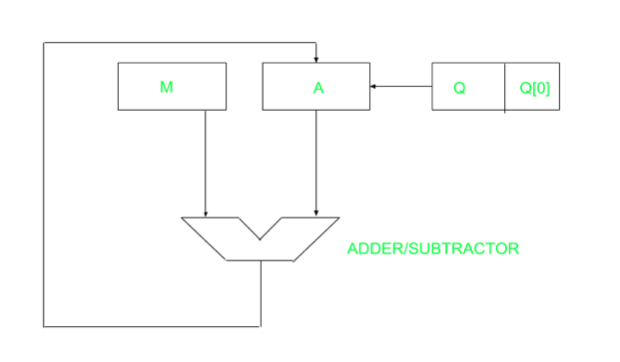
Fig 11 - Example
Here, register Q contains quotient and register A contains remainder. Here, the n-bit dividend is loaded in Q, and the divisor is loaded in M. Value of Register is initially kept 0 and this is the register whose value is restored during iteration due to which it is named Restoring.
Let’s pick the step involved:
● Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
● Step-2: Then the content of register A and Q is shifted left as if they are a single unit
● Step-3: Then the content of register M is subtracted from A and the result is stored in A
● Step-4: Then the most significant bit of the A is checked if it is 0 the least significant bit of Q is set to 1 otherwise if it is 1 the least significant bit of Q is set to 0 and the value of register A is restored i.e., the value of A before the subtraction with M
● Step-5: The value of counter n is decremented
● Step-6: If the value of n becomes zero, we get of the loop otherwise we repeat from step 2
● Step-7: Finally, the register Q contains the quotient, and A contain remainder
Examples:
Perform Division Restoring Algorithm
Dividend = 11
Divisor = 3
n | M | A | Q | Operation |
4 | 00011 | 00000 | 1011 | initialize |
| 00011 | 00001 | 011_ | shift left AQ |
| 00011 | 11110 | 011_ | A=A-M |
| 00011 | 00001 | 0110 | Q [0] =0 And restore A |
3 | 00011 | 00010 | 110_ | shift left AQ |
| 00011 | 11111 | 110_ | A=A-M |
| 00011 | 00010 | 1100 | Q [0] =0 |
2 | 00011 | 00101 | 100_ | shift left AQ |
| 00011 | 00010 | 100_ | A=A-M |
| 00011 | 00010 | 1001 | Q [0] =1 |
1 | 00011 | 00101 | 001_ | shift left AQ |
| 00011 | 00010 | 001_ | A=A-M |
| 00011 | 00010 | 0011 | Q [0] =1 |
Remember to restore the value of A most significant bit of A is 1. As that register Q contains the quotient, i.e., 3 and register A contain remainder 2.
Q11) Explain floating arithmetic?
A11) Floating-point arithmetic
The objectives of this module are to discuss the need for floating-point numbers, the standard representation used for floating-point numbers, and discuss how the various floating-point arithmetic operations of addition, subtraction, multiplication, and division are carried out.
Floating-point numbers and operations
Representation
When you have to represent very small or very large numbers, a fixed-point representation will not do. The accuracy will be lost. Therefore, you will have to look at floating-point representations, where the binary point is assumed to be floating. When you consider a decimal number 12. 34 * 107, this can also be treated as 0. 1234 * 109, where 0. 1234 is the fixed-point mantissa. The other part represents the exponent value and indicates that the actual position of the binary point is 9 positions to the right (left) of the indicated binary point in the fraction. Since the binary point can be moved to any position and the exponent value adjusted appropriately, it is called a floating-point representation. By convention, you generally go in for a normalized representation, wherein the floating-point is placed to the right of the first nonzero (significant) digit. The base need not be specified explicitly and the sign, the significant digits, and the signed exponent constitute the representation.
The IEEE (Institute of Electrical and Electronics Engineers) has produced a standard for floating-point arithmetic. This standard specifies how single-precision (32 bit) and double-precision (64 bit) floating-point numbers are to be represented, as well as how arithmetic should be carried out on them. The IEEE single-precision floating-point standard representation requires a 32-bit word, which may be represented as numbered from 0 to 31, left to right. The first bit is the sign bit, S, the next eight bits are the exponent bits, ‘E’, and the final 23 bits are the fraction ‘F’. Instead of the signed exponent E, the value stored is an unsigned integer E’ = E + 127, called the excess-127 format. Therefore, E’ is in the range 0 £ E’ £ 255.
S E’E’E’E’E’E’E’E’ FFFFFFFFFFFFFFFFFFFFFFF
0 1 8 9 31
The value V represented by the word may be determined as follows:
● If E’ = 255 and F is nonzero, then V = NaN (“Not a number”)
● If E’ = 255 and F is zero and S is 1, then V = -Infinity
● If E’ = 255 and F is zero and S is 0, then V = Infinity
● If 0 < E< 255 then V = (-1) **S * 2 ** (E-127) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
● If E’ = 0 and F is nonzero, then V = (-1) **S * 2 ** (-126) * (0. F). These are “unnormalized” values.
● If E’= 0 and F is zero and S is 1, then V = -0
● If E’ = 0 and F is zero and S is 0, then V = 0
For example,
0 00000000 00000000000000000000000 = 0
1 00000000 00000000000000000000000 = -0
0 11111111 00000000000000000000000 = Infinity
1 11111111 00000000000000000000000 = -Infinity
0 11111111 00000100000000000000000 = NaN
1 11111111 00100010001001010101010 = NaN
0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1. 0 = 2
0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1. 101 = 6. 5
1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1. 101 = -6. 5
0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1. 0 = 2**(-126)
0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0. 1 = 2**(-127)
0 00000000 00000000000000000000001 = +1 * 2**(-126) *
0. 00000000000000000000001 = 2**(-149) (Smallest positive value)
(Unnormalized values)
Double Precision Numbers:
The IEEE double-precision floating point standard representation requires a 64-bit word, which may be represented as numbered from 0 to 63, left to right. The first bit is the sign bit, S, the next eleven bits are the excess-1023 exponent bits, E’, and the final 52 bits are the fraction ‘F’:
S E’E’E’E’E’E’E’E’E’E’E’
FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
0 1 11 12
63
The value V represented by the word may be determined as follows:
● If E’ = 2047 and F is nonzero, then V = NaN (“Not a number”)
● If E’= 2047 and F is zero and S is 1, then V = -Infinity
● If E’= 2047 and F is zero and S is 0, then V = Infinity
● If 0 < E’< 2047 then V = (-1) **S * 2 ** (E-1023) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
● If E’= 0 and F is nonzero, then V = (-1) **S * 2 ** (-1022) * (0. F) These are “unnormalized” values.
● If E’= 0 and F is zero and S is 1, then V = – 0
● If E’= 0 and F is zero and S is 0, then V = 0
Arithmetic unit
Arithmetic operations on floating-point numbers consist of addition, subtraction, multiplication, and division. The operations are done with algorithms similar to those used on sign-magnitude integers (because of the similarity of representation) — for example, only add numbers of the same sign. If the numbers are of opposite sign, must do subtraction.
ADDITION
Example on decimal value given in scientific notation:
3. 25 x 10 ** 3
+ 2. 63 x 10 ** -1
—————–
first step: align decimal points
second step: add
3. 25 x 10 ** 3
+ 0. 000263 x 10 ** 3
——————–
3. 250263 x 10 ** 3
(Presumes the use of infinite precision, without regard for accuracy)
third step: normalize the result (already normalized!)
Example on floating pt. the value is given in binary:
. 25 = 0 01111101 00000000000000000000000
100 = 0 10000101 10010000000000000000000
To add this fl. pt. representations,
step 1: align radix points
shifting the mantissa left by 1 bit decreases the exponent by 1
shifting the mantissa right by 1 bit increases the exponent by 1
we want to shift the mantissa right because the bits that fall off the end should come from the least significant end of the mantissa
-> choose to shift the. 25 since we want to increase its exponent.
-> shift by 10000101
-01111101
———
00001000 (8) places.
0 01111101 00000000000000000000000 (original value)
0 01111110 10000000000000000000000 (shifted 1 place)
(Note that hidden bit is shifted into msb of mantissa)
0 01111111 01000000000000000000000 (shifted 2 places)
0 10000000 00100000000000000000000 (shifted 3 places)
0 10000001 00010000000000000000000 (shifted 4 places)
0 10000010 00001000000000000000000 (shifted 5 places)
0 10000011 00000100000000000000000 (shifted 6 places)
0 10000100 00000010000000000000000 (shifted 7 places)
0 10000101 00000001000000000000000 (shifted 8 places)
step 2: add (don’t forget the hidden bit for the 100)
0 10000101 1. 10010000000000000000000 (100)
+ 0 10000101 0. 00000001000000000000000 (. 25)
—————————————
0 10000101 1. 10010001000000000000000
step 3: normalize the result (get the “hidden bit” to be a 1)
It already is for this example.
result is 0 10000101 10010001000000000000000
SUBTRACTION
Same as addition as far as alignment of radix points
Then the algorithm for the subtraction of sign mag. numbers takes over.
Before subtracting,
Compare magnitudes (don’t forget the hidden bit!)
Change sign bit if the order of operands is changed.
Don’t forget to normalize the number afterward.
MULTIPLICATION
Example on decimal values given in scientific notation:
3. 0 x 10 ** 1
+ 0. 5 x 10 ** 2
—————–
Algorithm: multiply mantissas
add exponents
3. 0 x 10 ** 1
+ 0. 5 x 10 ** 2
—————–
1. 50 x 10 ** 3
Example in binary: Consider a mantissa that is only 4 bits.
0 10000100 0100
x 1 00111100 1100

Add exponents:
always add true exponents (otherwise the bias gets added in twice)
DIVISION
It is similar to multiplication.
Do unsigned division on the mantissa (don’t forget the hidden bit)
Subtract TRUE exponents
The organization of a floating-point adder unit and the algorithm is given below.
The floating-point multiplication algorithm is given below. A similar algorithm based on the steps discussed before can be used for division.
Q12) What do you mean by rounding?
A12) Routing
The floating-point arithmetic operations discussed above may produce a result with more digits than can be represented in 1. M. In such cases, the result must be rounded to fit into the available number of M positions. The extra bits that are used in intermediate calculations to improve the precision of the result are called guard bits.
It is only a tradeoff of hardware cost (keeping extra bits) and speed versus accumulated rounding error because finally, these extra bits have to be rounded off to conform to the IEEE standard.
Rounding Methods:
● Truncate
– Remove all digits beyond those supported
– 1. 00100 -> 1. 00
● Round up to the next value
– 1. 00100 -> 1. 01
● Round down to the previous value
– 1. 00100 -> 1. 00
– Differs from Truncate for negative numbers
● Round-to-nearest-even
– Rounds to the even value (the one with an LSB of 0)
– 1. 00100 -> 1. 00
– 1. 01100 -> 1. 10
– Produces zero average bias
– Default mode
A product may have twice as many digits as the multiplier and multiplicand
– 1. 11 x 1. 01 = 10. 0011
For round-to-nearest-even, we need to know the value to the right of the LSB (round bit) and whether any other digits to the right of the round digit are 1’s (the sticky bit is the OR of these digits). The IEEE standard requires the use of 3 extra bits of less significance than the 24 bits (of mantissa) implied in the single-precision representation – guard bit, round bit, and sticky bit. When a mantissa is to be shifted to align radix points, the bits that fall off the least significant end of the mantissa go into these extra bits (guard, round, and sticky bits). These bits can also be set by the normalization step in multiplication, and by extra bits of the quotient (remainder) in the division.
The guard and round bits are just 2 extra bits of precision that are used in calculations. The sticky bit is an indication of what is/could be in lesser significant bits that are not kept. If a value of 1 ever is shifted into the sticky bit position, that sticky bit remains a 1 (“sticks” at 1), despite further shifts.
To summarize, in his module we have discussed the need for floating-point numbers, the IEEE standard for representing floating-point numbers, Floating-point addition/subtraction, multiplication, division, and the various rounding methods.