Unit - 5

Advanced Topics

Q1) Define Heuristic Algorithm?

A1) An Approximate Algorithm is a way of approaching the optimization problem of NP-COMPLETENESS. This approach does not guarantee the right solution. The purpose of an approximation algorithm is to get as close as possible in a reasonable amount of time to the optimum value, which is at the most polynomial moment. These algorithms are called approximation algorithms or heuristic algorithms.

Q2) What is Heuristics function?

A2) Heuristic is a function which is used in Informed Search, and it finds the most promising path. It takes the current state of the agent as its input and produces the estimation of how close agent is from the goal. The heuristic method, however, might not always give the best solution, but it guaranteed to find a good solution in reasonable time. Heuristic function estimates how close a state is to the goal. It is represented by h(n), and it calculates the cost of an optimal path between the pair of states. The value of the heuristic function is always positive.

Q3) What are the types of Approximation Algorithm?

A3) There are two types of Approximation: -

A is an absolute approximation algorithm if a constant k exists. Such that I, of P, for every case, |A∗ (I) − A(I)| ≤ k.

Planar graph colouring, for instance.

●      A is a relative approximation algorithm if there exists a constant k Such that I, of P, for every case,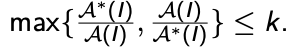 

●      Vertex cover

Example:

1. Vertex Cover

2. Traveling Salesman Problem

3. Bin Packing

Q4) Define Vertex Cover? With the suitable example?

A4) A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.

In a given undirected graph we need to find the maximum size of vertex cover.

It is the optimization version of NP complete problems.

It is easy to find vertex cover.

Example:

Given graph with set of edges are 

{(1,6), (1,2), (1,4), (2,3), (2,4), (6,7), (4,7), (7,8), (3,8), (3,5), (8,5)}

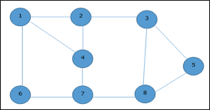
Now, start by selecting an edge (1, 6).

Eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1, 6) to cover.

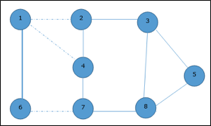
In the next step, we have chosen another edge (2, 3) at random

Now we select another edge (4, 7).

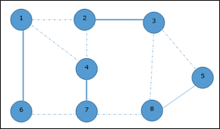
We select another edge (8, 5).

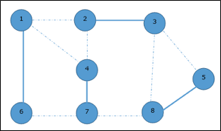
Hence, the vertex cover of this graph is {1, 2, 4, 5}.

Analysis of Vertex Cover Algorithm

In this algorithm, by using an adjacency list to represent E it is easy to see the running time of this algorithm is O (V+E).

Q5) Describe Travelling Salesman Problem? In brief.

A5) In the traveling salesman Problem, a salesman must visit n cities. We can say that salesman wishes to make a tour or Hamiltonian cycle, visiting each city exactly once and finishing at the city he starts from. There is a non-negative cost c (i, j) to travel from the city i to city j. The goal is to find a tour of minimum cost. We assume that every two cities are connected. Such problems are called Traveling-salesman problem (TSP).

We can model the cities as a complete graph of n vertices, where each vertex represents a city.

It can be shown that TSP is NPC.

If we assume the cost function c satisfies the triangle inequality, then we can use the following approximate algorithm.

Triangle inequality

Let u, v, w be any three vertices, we have

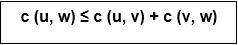
One important observation to develop an approximate solution is if we remove an edge from H*, the tour becomes a spanning tree.

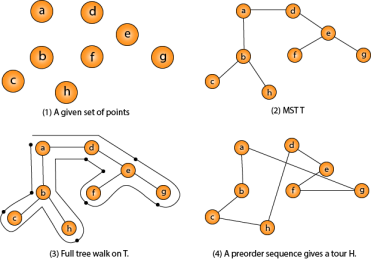
Fig - Traveling-salesman Problem

Intuitively, Approx-TSP first makes a full walk of MST T, which visits each edge exactly two times. To create a Hamiltonian cycle from the full walk, it bypasses some vertices

Q6) Define Bin packing?

A6) In case of given m elements of different weights and bins each of capacity C, assign each element to a bin so that number of total implemented bins is minimized. Assumption should be that all elements have weights less than bin capacity.

Applications

Example

Input: weight [] = {4, 1, 8, 1, 4, 2}

Bin Capacity c = 10

Output: 2

We require at least 2 bins to accommodate all elements

First bin consists {4, 4, 2} and second bin {8, 2}

Q7) Defined Randomized algorithms?

Q9) Define Las Vegas? With an example?

A10) These algorithms produce the correct or optimum result on the basis of probability. Monte Carlo algorithm has deterministic running time and it is generally easier to find out worst case time complexity.