Unit - 1
Sets and propositions
Q1) Define principle of inclusion and exclusion.
A1) The Inclusion-Exclusion principle can be stated as below-
Let A and B any two finite sets, then-
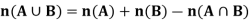
Meaning- Here if we have to find the number 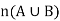 of elements in the union of A and B.
of elements in the union of A and B.
So, then we add n(A) and n(B) which means we are including these two.
And then we exclude  .
.
Note- For three sets-
If we have three finite sets A, B and C then-

Q2) 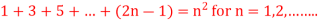
A2) Here for n = 1, 1 = 1²
Now let us assume that the statement is true for n = k
Hence, we assume that 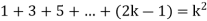 is true.
is true.
Now we need to prove that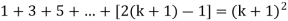
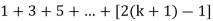

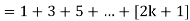
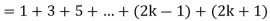

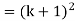
So that  which satisfies the second step.
which satisfies the second step.
Hence-
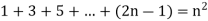
Q3) Prove 1+2+...+n=n(n+1)/2 using a proof by induction
A3) Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,
Step-1: Assume n=k holds: 1+2+...+k=k(k+1)/2
Show n=k+1 holds: 1+2+...+k+(k+1) =(k+1) ((k+1) +1)/2
Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.
Step-2: Now start with the left side of the equation
1+2+...+(k+1) =1+2+...+k+(k+1)
=k(k+1)/2 + (k+1)
=(k(k+1) + 2(k+1))/2 by 2/2=1 and distribution of division over addition
=(k+2) (k+1)/2 by distribution of multiplication over addition
=(k+1) (k+2)/2 by commutativity of multiplication.
Q4) Define statement.
A4) When a declarative sentence which is true or false but not both is called statement.
The truth values “true” and “false” of a statement are denoted by T ad F respectively. We can denote them by 0 and 1 as well.
Examples of statements are-
1. 2 + 11 = 12
2. Jaipur is in India
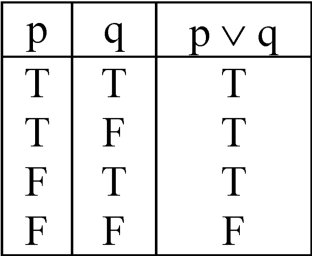
Q5) What is disjunction?
A5) The disjunction of two propositions p and q is the compound statement 10 Elementary Logic p or q, denoted by p ∨ q.
For example, ‘Aman has a house or Amit has a house’ Is the disjunction of p and q, where-
p: Aman has a house, and
q: Amit has a house.
Q6) Obtain the truth value of the disjunction of ‘The earth is flat’. and ‘3 + 5 = 2’.
A6) Let p denote ‘The earth is flat,’ and q denote ‘3 + 5 = 2’. Then we know that the truth values of both p and q are F. Therefore, the truth value of p ∨ q is F.
Q7) Let p: 5 + 2 = 7, q: 9 + 2 = 10 then p ∨q: 5 + 2 = 7 or 9 + 2 = 10
A7) Truth table for disjunction-
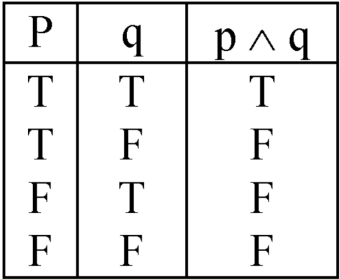
Q8) Define conjunction.
A8) We call the compound statement ‘p and q’ the conjunction of the
Statements p and q. We denote this by p ∧q.
Example- ‘3 + 1 ≠ 7 ∧ 2 > 0’ is the conjunction of ‘3 + 1 ≠ 7’ and ‘2 > 0’.
Q9) Obtain the truth value of the conjunction of ‘2 ÷5 = 1’ and ‘Ramesh is in Jaipur’.
A9) Let p: 2 ÷5 = 1, and
q: Ramesh is in Jaipur.
Then the truth value of p is F. Therefore, from Table 3 you will find that the truth
Value of p ∧ q is F.
Q10) What are conditional connectives?
A10) Given any two propositions p and q, we denote the statement ‘If p, then q’ by
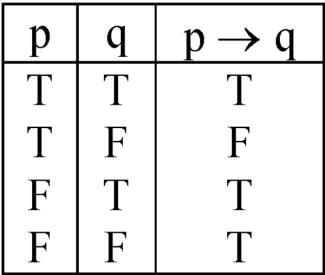
p→ q. We also read this as ‘p implies q’. or ‘p is sufficient for q’, or ‘p only if q’. We also call p the hypothesis and q the conclusion. Further, a statement of the form p → q is called a conditional statement.
Truth table for implication-
Q11) Pradeep will get good marks if and only if he studies regularly means that Pradeep will get good marks if he studies regularly and Pradeep studies regularly if he gets good marks.
A11) Truth table for two-way implication-

Q12) Define proposition and compound proposition.
A12) Proposition- A proposition (or statement) is a declarative statement which is true or false, but not both.
Example-
(i) Ice floats in water.
(ii) China is in Europe
(iii) 2 + 2 = 4
(iv) 2 + 2 = 5
Compound proposition-
Many propositions are composite, that is, composed of sub-propositions and various connectives discussed
Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive
If it cannot be broken down into simpler propositions, that is, if it is not composite.
Following two propositions are composite:
“Roses are red and violets are blue.” and “John is smart or he studies every night.”
Q13) What do you understand by negation?
A13) Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
Q14) What are universal quantifiers? Explain
A14) Let us consider the following proposition-
‘Every rational number is a real number’ can be re-written as. For every x, if x is a rational and number, then x is a real number. The phrase ‘for every x’ is called a universal quantifier.
Or
Let p(x) is a propositional function defined on a set A, consider the expression

Here the symbol which we read “for all” or “for every” is called universal quantifier.
The above statement can be written as-
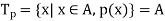
That is, that the truth set of p(x) is the entire set A.
The expression p(x) is a condition itself and it has no truth value
It is symbolically denoted by 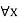 .
.
If P (x) denotes a predicate, then the universal quantification for P (x), is the statement.
“For all values of x, P (x) is true”
Q15) Define existential quantifiers.
A15) Existential quantifiers:
The existential quantification for a predicate is the statement “There exists a value of x” for which P (x). The symbol 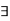 , is used to denote the logical quantifier ‘there exists’ the phrases ‘There exists an x’, ‘There is a x’, for some x’ and ‘for at least one x’ have the same meaning. The existential quantifier for P (x) is denoted by
, is used to denote the logical quantifier ‘there exists’ the phrases ‘There exists an x’, ‘There is a x’, for some x’ and ‘for at least one x’ have the same meaning. The existential quantifier for P (x) is denoted by  x P (x).
x P (x).
Or
Let p(x) be a propositional function defined on a set A. consider an expression-
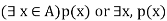
The symbol 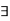 reads as there exists is called existential quantifier.
reads as there exists is called existential quantifier.
Q16) Explain direct proof method.
A16) This method is totally based on modus ponens.
We assume that P is true, and from the available information the conclusion q is shown to be true by valid reference.
We construct a chain of statements P,  . where P is either a hypothesis of the theorem or an axiom and each of the implications
. where P is either a hypothesis of the theorem or an axiom and each of the implications
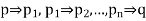
is either an axiom or is implied by the implication preceding it.
Q17) The product of two odd integers is odd.
A17) Let consider there are two odd integers x and y, so our hypothesis is-
P: x and y are odd
We want to reach the conclusion-
q: xy is odd
let us first prove that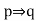
here x is odd, x = 2m + 1 for some integer m.
And y = 2n + 1 for some integers n.
Then-
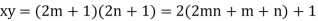
Therefore, xy is odd
So, it is shown that-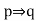
Q18) If x is a number such that 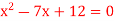 then show that x = 3, x = 4 by direct proof.
then show that x = 3, x = 4 by direct proof.
A18) 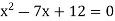 can be written as-
can be written as-
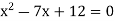
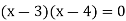
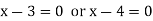

Hence 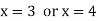
Q19) For any integer n > 2, prove that n Prime  n odd.
n odd.
A19) Let
p: n Prime
q: n odd
then
~ q: n even
~ p: n not primes
If n is an even number greater than 2, then n = 2m for some integer m > 1. Thus, n is divisible by 2 and n 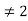 therefore n cannot be prime thus we have ~q
therefore n cannot be prime thus we have ~q 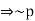
Which means if n is any number bigger than 2, then n cannot be prime.
Q20) Prove that 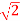 is an irrational number.
is an irrational number.
A20) Let us suppose  is a rational number, then-
is a rational number, then-
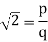
Where p and q have no common factor.
Now square on both sides-

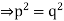
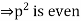
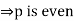
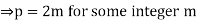

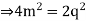


Hence p and q have common factor of 2, which is a contradiction to the statement that a and b have no common factors.
Hence our assumption that 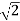 is rational leads to a contradiction. Thus
is rational leads to a contradiction. Thus 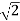 is irrational.
is irrational.