Unit - 3

Numeric Functions and Generating Functions

Q1) Define numeric function.

A1)

The set of real numbers are called numeric function.

We use bold face lowercase letters to denote Numeric functions.

For example:

Is the numeric function where denotes the values a at 0,1,2, 3…...r……

Q2) Define forward and backward differences.

A2)

If

Then is called its forward difference at r.

We denote it by .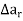

The backward difference is denoted by

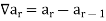
The convolution of two numeric function a and b is a numeric function c such that-

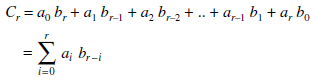
We denote the convolution of a and b by a * b

Q3) Explain generating function.

A3)

For a numeric function-

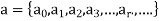
An infinite series is defined as-

  which is called the generating function of a.

We denote it by A(Z).

The coefficient of is A (z) is the value of the numeric function a.

For example:

If the generating function is

is

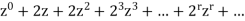
We can write the above series as below-

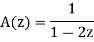
In   the term 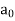is called the constant term.

Let

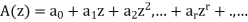
And

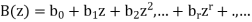
Are the generating functions.

A(z) and B(z) are equal if , for each

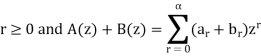
The product can be defined as-

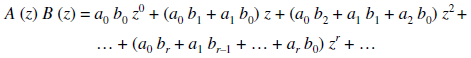
Q4) What do you understand by recurrence relation.

A4)

Recursion is a technique of defining a function, a set or an algorithm in terms of itself.

Suppose the set of natural numbers, we introduce the method of generating the set of natural numbers by recursion.

The natural numbers with zero are those objects which can be generated by starting with an initial object 0 and from any object “n” already generated passing to another uniquely determined object , the successor of n. The objects differently generated are always distinct. Thus, the natural numbers appear as a set of objects 0,

The transition to the usual notation is made upon introducing 1, 2, 3, 4, … to stand for and then employing the notation.

 The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.

Q5) Find a recurrence relation and initial conditions for 1, 5, 17, 53, 161, 485.

A5)

Here is the recurrence relation and the initial condition is

Q6) Check whether 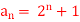is a solution to the recurrence relation 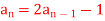with .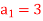

A6)

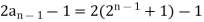
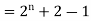
Q7) Explain linear recurrence relation with constant coefficient.

A7)

If 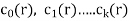are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.

A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

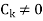Where are constant with and f(n) is a function of ’n’.

Q8) Consider a following recurrence relation-

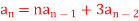
A8)

It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of is not a constant given initial conditions 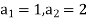, the next elements of the sequence follow-

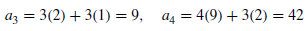
Q9) Solve the recurrence relation-

A9)

Multiplying each term of the recurrence relation by 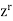, we find-

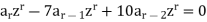
Now taking the sum to 2 to 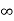, we get

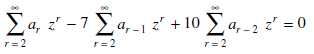
Replace each infinite sum by the corresponding equivalent expression given above, we obtain-

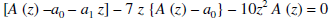
On simplifying, we obtain-

Decomposing A (z) as a sum of partial fractions, we can write

The solution is-

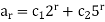
Q10) Explain the method generating functions.

A10)

Any numeric function that can be described by a recurrence relation together with an appropriate set of boundary conditions is called a solution of the recurrence relation.

If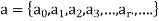
 

is a solution to a recurrence relation then it is said to satisfy the relation.

A given recurrence relation may or may not have a solution.

Method of generating functions-

Recurrence relations can also be solved by using generating functions. Some equivalent expressions used are given below-

Then