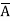Unit - 4

Groups and rings

Q1) Define groups.

A1)

A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:

Condition-1: For all a, b, c, ∈ G

a* (b * c) = (a * b) * c (associativity)

Condition-2: There exists an elements e ∈G such that for any a ∈G

a* e= e * a = a (existence of identity)

Condition-3: For every a ∈G, there exists an element denoted by 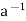in G such that

a* 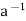= 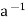* a = e

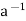is called the inverse of a in G.

Example: (Z, +) is a group where Z denote the set of integers.

Example: (R, +) is a group where R denote the set of real numbers.

Q2) Define abelian and finite group.

A2)

Abelian group-

Let (G, *) be a group. If * is commutative that is

a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.

Finite group-

A group G is said to be a finite group if the set G is a finite set.

Q3) If G = {1, -1, i, -i} where i = , then show that G is an abelian group with respect to multiplication as a binary operation.

A3)

First, we will construct a composition table-

It is clear from the above table that algebraic structure (G,.) is closed and satisfies the following conditions.

Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅ (b ⋅c)

Since

1 ⋅ (−1 ⋅i) = 1 ⋅−i= −i

(1 ⋅−1) ⋅i= −1 ⋅i= −i

⇒1 ⋅ (−1 ⋅i) = (1 ⋅−1) i

Similarly with any other three elements of G the properties hold.

∴ Associative law holds in (G, ⋅)

Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G

Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1

(−1) ⋅ (−1) = 1 = (−1) ⋅ (−1) ⇒–1 is the inverse of (–1)

i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.

−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.

Hence inverse of every element in G exists.

Thus, all the axioms of a group are satisfied.

Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G

1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1

i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.

Commutative law is satisfied.

Hence (G, ⋅) is an abelian group.

Q4) Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.

A4)

Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z

⇒a +b + 1 ⋅∈Z ∀a, b ∈Z

⇒Z is called with respect to *

Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as

(a* b) * c = (a + b + 1) * c

= a + b + 1 + c + 1

= a + b + c + 2

Also

a* (b * c) = a * (b + c + 1)

= a + b + c + 1 + 1

= a + b + c + 2

Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.

Q5) If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if

(i) a, b ∈H ⇒a * b ∈H;

(ii) a ∈ H ⇒∈H

A5)

Proof:

If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.

We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).

To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is: * is associative in

H and identity e ∈ H.

That * is associative in H follows from the fact that * is associative in G.

Also,

A ∈ H ⇒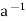∈H by (ii) and e ∈H and 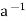∈H ⇒a * 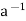= e ∈H by (i)

Hence, H is a sub-group of G.

Q6) Define cosets.

A6)

Let (H, *) be a sub-group (G, *) and a ∈G

Then the sub-set:

a* H = {a * h: h ∈H} is called a left coset of H in G, and the subset

H * G = {h * a: h ∈H} is called a right coset of H in G.

Q7) If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.

A7)

Proof: Let a * H = H

Since e ∈H then a = a * e ∈a * H

Hence a ∈H

Conversely

Let a ∈H then a * H ⊆H

(H, *) is a sub-group.

∴a ∈ H, h ∈ H ⇒ * h ∈ H.

Now h ∈H

⇒h = a * (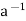 * h) ∈a * H

∴h ∈ H ⇒h ∈a * H

⇒H ⊆ a * H

Hence a * H = H

Q8) Define kernel of homomorphism.

A8)

Kernel of homomorphism-

Let G and G be any two groups and f: G →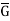be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = ).

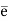Where e is the identity of .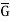

Q9) Let G be (Z, +) i.e., the group of integers under addition and let f: G → G defined by

∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.

A9)

We have ∅(x) = 3x ∀x ∈G

∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)

Now

f (x + y) = 3 (x + y)

= 3x + 3y

= f (x) + f (y)

Hence f is homomorphism.

Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.

Thus K = {0}

Q10) Show that (3, 7) encoding function e defined below is a group code.

e (000) =0000000  e (001) =0010110  e (010) =0101000

e (011) =0111110  e (100) =1000101  e (101) =1010011

e (110) =1101101  e (111) =1111011

How many errors can it detect?

A10)

From the diagonal elements of the above table, we see that (0000000) is an identity and it belongs to N.

From the table we also see that if x, y belongs to N then x  y belongs to N.

Every element is its inverse.

N is a subgroup of B7 and the given encoding function is a group code.

The minimum distance is 2. Hence, the code can detect 1 or less errors.

Q11) Let S be the set of all even integers. Show that the smi groups (Z, +) and (S, +) are isomorphic

A11)

Step 1: we define the function f: Z     S where f(a)=2a

Step 2: suppose f(a1) =f(a2). Then 2a1=2a2. Hence f is one to one

Step 3: Suppose b is an even integer. Then a=b/2 € Z and f(a)= f(b/2) = 2(b/2) =b. hence fits onto.

Step 4: We have f (a+b) = 2(a+b) = 2a+2b= f(a)+f(b)

Hence (Z, +) and (S, +) are isomorphic.

An isomorphism from a semi group (S, *) to (S, *) itself is called an automorphism (auto=self) on (S, *)

Q12) Define isomorphism and give steps to find isomorphism.

A12)

Let (s, *) and (S’, *) be two semi group. A function f: S    S’ is called an isomorphism if s is one to one and onto and if

f(a+b) =f(a)*f(b). for all a, b in S

Procedure to find the isomorphism

Step 1: we define the function f: S      S’ with domain of f=S

Step 2: We shall show that f is one to one.

Step 3: We shall show that f is onto.

Step 4: We shall show that f(a*b) = f(a)*’ f(b).

Q13) Prove that congruence modulo n is an equivalence relation on Z.

A13)

1) Reflexivity: For any a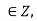we have 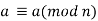because a-a = 0 is divisible by n. hence relation is reflexive.

2) Symmetry: suppose a b (mod n)

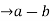is divisible by n 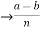= k, for some k z  a-b = nk

Therefore, b-a = -(a-b) = -nk= n(-k)

Thus, the relation is symmetric.

3) Transitivity: Suppose a b (mod n) and b c (mod n), then = k and

By adding these two equations we get, a-c = n(k+1) 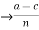= k+l

So, a-c is divisible by n as k+1 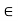Z, i.e., a c (mod n)

Thus, the relation is transitive.

Hence this is an equivalence relation on Z.

Q14) The cancellation laws hold in a ring R if and only if R has no divisors of 0.

A14)

Assume that R is a ring in which the cancellation laws hold and let ab=0 for some a,b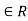 .If a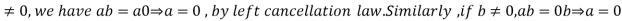 by right cancellation law .Thus R  has no divisors of 0, if the cancellation laws hold in R.

Conversely, suppose that R has no divisors of 0, and suppose that ab=ac, with a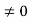. Since a 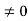and since R has no divisors of 0, we have 0=ab-ac=a(c) 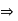b-c =0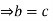.In similar way, b a=ca with a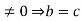. Thus, if R has no divisors of 0, the cancellation laws hold in R.

Q15) Define Boolean algebra.

A15)

A Boolean algebra is a distributed complemented lattice having at least two members as well as 0 and 1.

A Boolean algebra is denoted by .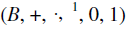

Here (B, +,.) is a lattice which has two binary operations + and., called the join and meet respectively is a unary operation in B.

The following axioms are satisfied-

2.     For every for all,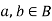

(i)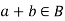               

(ii)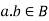             

3.     For all 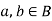[commutative laws]

(i)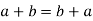               

(ii)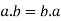             

4.     For all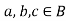 [associative law]

(i)               

(ii)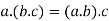             

5.     For all [distributive law]

(iii)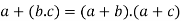          

(iv)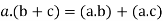           

6.     There exists of B such that-

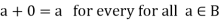
Element 0 is called the zero elements.

7.     There exists 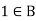sum that-

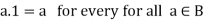
1 is called the unit element.

8.     Existence of complement- for every for all there exists an element 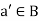such that-

(i)                a + a’ = 1    and    (ii) a.a’ = 0

(ii)               

Q16) What do you understand by lattice.

A16)

Lattices-

A lattice is a partially ordered set 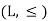in which every pair of elements a, b 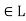has a greatest lower bound and a least upper bound

For example-

Suppose S be a non-empty set and L = P(S); 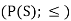that means ( 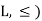is partially ordered.

If X and Y are two elements of L, then-

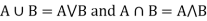
Hence (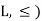 is a Lattice.

Q17) Simplify z (y+z) ((x + y + z).

A17)

z (y + z) (x + y + z)

= (z y + z z) (x + y + z)

= (z y + z) (x + y + z)

= z (y + 1) (x + y + z)

= z (x + y + z)

= z x + z y + z z

= z x + z y + z

= z (x + y + 1)

= z (x + 1)

= z

Q18) Minimize the expression ++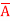 A B

A18)

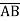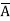+ + A B

= + + + A B

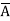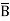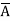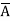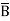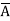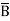= + + + A B

= + + A B

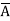= + A B +

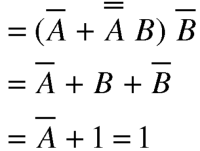
Hence

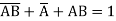
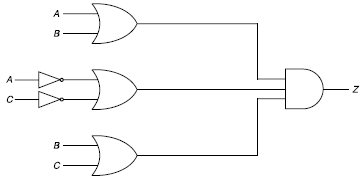
Q19) What will be logic circuit of the input-output Boolean expression-

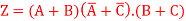
A19)

Q20)  Define NOT gate.

A20)

NOT-gate is one input and one output logic gate. The output of a NOT-gate is always the complement of the input. It is also known as an inverter or a complementing circuit

We symbolize NOT-gate with the following symbol-

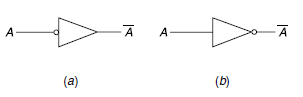
And the truth table is given as-