Unit - 5

Graphs and trees

Q1) Define graph.

A1)

A graph (V, E) is an ordered pair, whose V is finite non-empty set elements are called vertices and ‘E’ is a set of un-ordered pair of distinct vertices of ‘V’.

i.e. (V, E) – where V is Finite non-empty set

where is E is unordered pairs (edges)

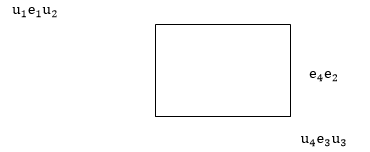
Example 1: 

2: V = 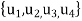 , E =

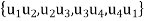
Q2) What are multi graph and Pseudo graph.

A2)

Multi Graph:

A multi graph G= (V, E) is an ordered pair of sets, where ‘V’ is finite and non-empty set and ‘E’ is set of un-ordered pairs of distinct elements of v and repetitions are allowed in the classes.

Pseudo Graph:

A Pseudo graph G= (V, E) is ordered pairs, where ‘v’ is finite and non-empty E is set of un-ordered pairs of distinct elements of V and repetitions are allowed in the classes.

 Note: Multi-graph and Pseudo-graph same but self-loop in the pseudo.

Q3) Define network.

A3)

A network is a dia-graph which possess exactly one source and one sink, the vertices of a network are called nodes.

Q4) What are bipartite graph.

A4)

A graph G (V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subsets 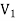and 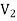such that each edge is G had end vertex is 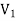and other end vertex in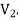

There is no edge between two vertices of 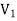as well as there is no edge between two vertices of .

Here 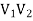bipartition of V.

Q5) Consider the graphs given below-

 Check whether these graphs are same or not?

A5)

As we can see that these graphs are not same because here 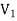and 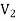are not same since 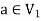but a does not belongs to .

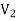These two graphs look same but not equal.

We can draw these graphs as below-

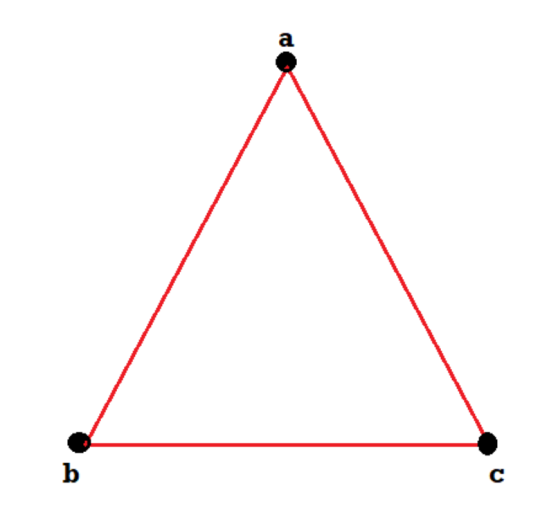
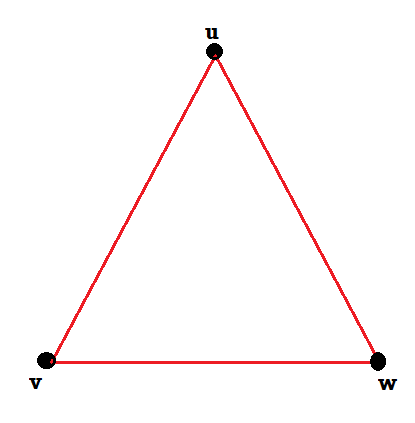
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.

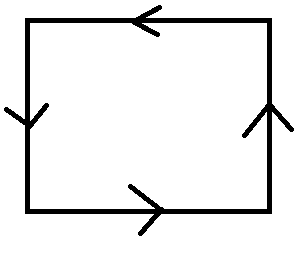
Q6) What do you understand by digraph.

A6)

Let G = (V, E) be a graph. If the elements of E are ordered pairs of vertices, then the graph G is called a directed graph.

The vertex u is called the origin or initial point of the directed edge e and v is called the destination or terminal point of e.

The example of the digraph is-

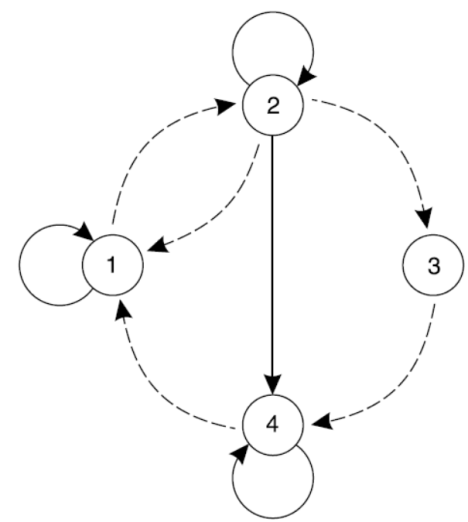
Q7) Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 4)}

Represent the relation by graph.

A7)

The diagraph of R can be made as-

Q8) Are the two following graphs are isomorphic?

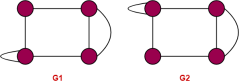
A8)

We check the necessary and sufficient conditions for the given graphs to be isomorphic

Condition 1: number of vertices in G1 =4

Number of vertices in G2= 4

Here both G1 and G2 have same number of vertices hence the condition satisfied.

Condition 2: number of edges in G1 = 5

Number of edges in G2 = 6

Here they are not equal, therefore the condition is not satisfied.

Hence the given graphs are not isomorphic.

Q9) Define connectivity.

A9)

A graph is a connected graph if, for each pair of vertices, there exists at least one single path which joins them. A connected graph may demand a minimum number of edges or vertices which are required to be removed to separate the other vertices from one another. The graph connectivity is the measure of the robustness of the graph as a network.

In a connected graph, if any of the vertices are removed, the graph gets disconnected. Then the graph is called a vertex-connected graph. On the other hand, when an edge is removed, the graph becomes disconnected. It is known as an edge-connected graph.

Q10) If a complete graph has a total of 20 vertices, then find the number of edges it may contain.

A10)

The formula for the total number of edges in a k15 graph is given by;

Number of edges =

=

=10(19)

=190

Hence, it contains 190 edges.

Q11) If a graph has 40 edges, then how many vertices does it have?

A11)

As we know,

Number of edges = =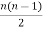

40 =

n(n-1) = 80

n2 – n – 80 = 0

On solving the above quadratic equation, we get;

n ≈ 9.45, -8.45

Since, the number of vertices cannot be negative.

Therefore, n ≈ 9

Q12) Define graph traversal.

A12)

A multigraph is said to be traversable if it “can be drawn without any breaks in the curve and without repeating any edges,” that is, if there is a path which includes all vertices and uses each edge exactly once.

Or in other words-

A graph G is said to be traversable, if it has a path.

Q13) Explain Hamiltonian graph.

A13)

Hamiltonian graph- A closed path that visits every vertex in G exactly once and if G admit a Hamiltonian circuit, then G is called Hamiltonian graph.

Note- An Eulerian circuit traverses every edge exactly once, but many repeats’ vertices.

While a Hamiltonian circuit visits each vertex exactly once but many repeats edges.

Following are the examples of Hamiltonian and Eulerian graph respectively-

Note:

Q14) Explain why every tree is a bipartite graph.

A14)

To show that a graph is bipartite, we must divide the vertices into two sets A and B so that no two vertices in the same set are adjacent. Here is an algorithm that does just this.

Designate any vertex as the root. Put this vertex in set A. Now put all of the children of the root in set B. None of these children are adjacent (they are siblings), so we are good so far. Now put into A every child of every vertex in B (i.e., every grandchild of the root). Keep going until all vertices have been assigned one of the sets, alternating between A and B every “generation.” That is, a vertex is in set B if and only if it is the child of a vertex in set A.

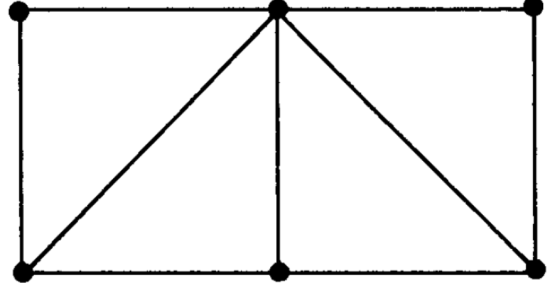
Q15) Find two different spanning trees of the graph.

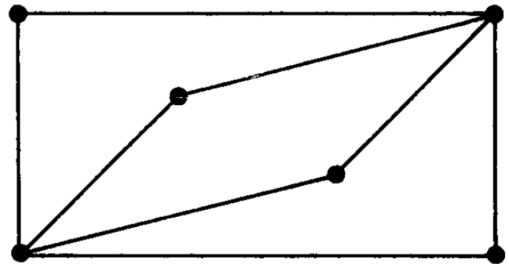
A15)

Two spanning trees are-

And

Q16) Prove that there are 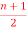pendent vertices in any binary tree with ‘n’ vertices.

A16)

Suppose T = (V, E) be a binary tree with ‘n’ vertices. Let ‘m’ be the two no. of pendent vertices in T. Then T has (n-(m+1)) no. of internal vertices of degree 3

So, the sum of degree of all vertices in T is 3(n-m-1) + m+2…. (1)

Since T is tree with ’n’ vertices then it has (n-1) edges.

So, the degree sum of ‘n’ vertices in T is given by

(2)

From (1) and (2)

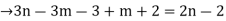
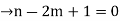
  The no. of pendent vertices in binary tree is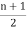 

Q17) For instance, identify the minimum spanning tree from the following graph G by using the Kruskal’s algorithm.

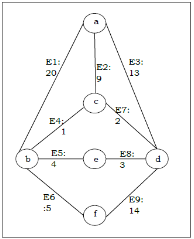
A17)

The following table is constructed from the above graph:

In accordance with the weight of the Edge, the table is rearranged in ascending order.

We get the required minimal spanning tree

Step-1:

Step-2:

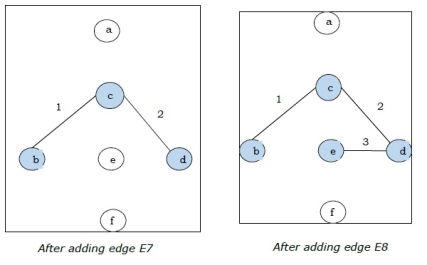
Step-3:

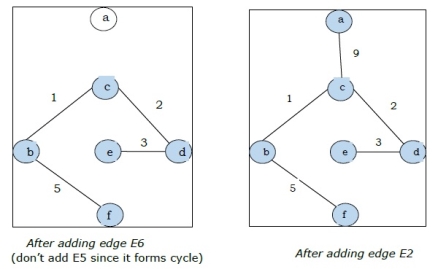
As all the edges are covered in the last figure, the algorithm is stopped and this is considered as the minimal spanning tree and the total weight of the spanning tree is (1+2+3+5+9) =20.