Unit - 4

Push Down Automata (PDA)

Q1) Define PDA?

A1) It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically, a pushdown automaton is -

“Finite state machine” + “a stack”

A pushdown automaton has three components −

●      An input tape,

●      A control unit, and

●      A stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

●      Push − a new symbol is added at the top.

●      Pop − the top symbol is read and removed.

A PDA may or may not read an input symbol, but it has to read the top of the stack in

Every transition.

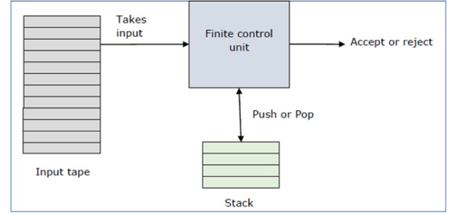
Fig: Basic structure of PDA

A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0, I, F) −

Where

●      Q is the finite number of states

●      ∑ is input alphabet

●      S is stack symbols

●      δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*)

●      q 0  is the initial state (q 0  ∈ Q)

●      I is the initial stack top symbol (I ∈ S)

●      F is a set of accepting states (F ∈ Q)

The following diagram shows a transition in a PDA from a state q 1 to state q 2, labeled as a, b → c −

Fig: Example

This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2 .

Q2) What is an instantaneous description?

A2) Instantaneous description (ID) is a colloquial term for how a PDA computes an input string and decides whether it should be accepted or rejected.

A triplet (q, w, s) represents the instantaneous description (ID) of a PDA -

●      q is the state

●      w is unconsumed input

●      s is the stack contents

Turnstile Notation

For connecting pairs of IDs that represent one or more PDA moves, the "turnstile" notation is employed. The turnstile symbol "⊢” represents the changeover process.

Consider a personal digital assistant (PDA) (Q, ∑, S, δ, q0, I, F). The turnstile notation can be used to depict a transition mathematically.

(p, aw, Tβ) ⊢ (q, w, αb)

This means that the input symbol ‘a' is consumed during the transition from state p to state q, and the top of the stack ‘T' is replaced by a new string “α’'.

Example: Create a PDA that can accept the language {0n1m0n | m, n>=1}.

Solution: In this PDA, n number of 0s are followed by any number of 1‘s, which are then followed by n number of 0’s. As a result, the design reasoning for such a PDA will be as follows:

When you come to the first 0's, push all of the 0's onto the stack. Then, if we read number one, we should do nothing. Then read 0 and pop one 0 from the stack for each read of 0.

For instance:

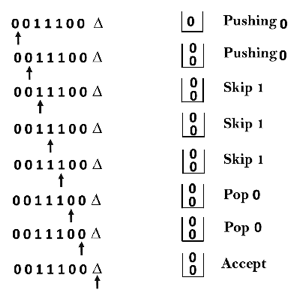
In ID form, this circumstance is as follows:

δ(q0, 0, Z) = δ(q0, 0Z) 

δ(q0, 0, 0) = δ(q0, 00) 

δ(q0, 1, 0) = δ(q1, 0) 

δ(q0, 1, 0) = δ(q1, 0) 

δ(q1, 0, 0) = δ(q1, ε) 

δ(q0, ε, Z) = δ(q2, Z)      (ACCEPT state) 

For the input string "0011100," we'll now replicate this PDA.

δ (q0, 0011100, Z) ⊢ δ (q0, 011100, 0Z) 

⊢ δ (q0, 11100, 00Z) 

⊢ δ (q0, 1100, 00Z) 

⊢ δ (q1, 100, 00Z) 

⊢ δ (q1, 00, 00Z) 

⊢ δ (q1, 0, 0Z) 

⊢ δ (q1, ε, Z) 

⊢ δ (q2, Z) 

ACCEPT

Q3) What do you mean by acceptance by final state?

A3) When a PDA accepts a string in final state acceptability, the PDA is in a final state after reading the full string. We can make moves from the starting state to a final state with any stack values. As long as we end up in a final state, the stack values don't matter.

If the PDA enters any final state in zero or more moves after receiving the complete input, it is said to accept it by the final state.

Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by the final state can be defined as:

L(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ F} 

Equivalence of Acceptance by Final State and Empty Stack

There is a PDA P2 such that L = L (P2) if L = N(P1) for some PDA P1. That is, the language supported by the empty stack PDA will be supported by the end state PDA as well.

If a language L = L (P1) exists for a PDA P1, then L = N (P2) exists for a PDA P2. That is, language supported by the end state PDA is also supported by the empty stack PDA.

Q4) Explain acceptance by empty stack?

A4) The stack of PDAs becomes empty after reading the input string from the initial setup for some PDA.

When a PDA has exhausted its stack after reading the entire string, it accepts a string.

Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by empty stack can be defined as:

N(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ Q} 

Example

Construct a PDA that accepts L = {0n 1n | n ≥ 0}

Solution:

This language accepts L = {ε, 01, 0011, 000111, ............................. }

The number of ‘a' and ‘b' in this example must be the same.

●      We began by inserting the special symbol ‘$' into the empty stack.

●      If we encounter input 0 and top is Null at state q2, we push 0 into the stack. It's possible that this will happen again. We pop this 0 if we meet input 1 and top is 0.

●      If we encounter input 1 at state q3 and the top is 0, we pop this 0. It's possible that this will continue to iterate. We pop the top element if we meet input 1 and top is 0.

●      If the special symbol '$' appears at the top of the stack, it is popped out, and the stack eventually moves to the accepting state q4.

Q5) Describe deterministic PDA?

A5) Machine transitions are based on the actual state and input symbol, as well as the stack's current uppermost symbol. 

●      The lower symbols in the stack are not apparent and do not have an immediate effect.

●      The acts of the computer include pushing, popping or replacing the top of the stack.

●      For the same combination of input symbol, state, and top stack symbol, a deterministic pushdown automaton has at most one legal transformation.

●      This is where the pushdown automaton varies from the nondeterministic one.

●      DPDA is a subset of context-free language.

A deterministic pushdown automata M can be defined as 7 tuples -

M = (Q, ∑, T, q0, Z0, A, δ)

Where,

●      Q is a finite set of states,

●      ∑ is finite set of input symbol,

●      T is a finite set of stack symbols,

●      q0 ∈ Q is a start state,

●      Z0 ∈ T is the starting stack symbol,

●      A ⊆ Q, where A is a set of accepting states,

●      δ is a transition function, where:

δ :(Q X (∑ U {ε}) X  T ) ➝ p(Q  X T* )

Q6) Write the equivalence of PDA and CFG?

A6) Equivalence of PDA and CFG

●      The three types of languages that follow are all the same.

1. CFG-defined languages, i.e., context-free languages.
2. The languages that are accepted by some PDAs in their final state.
3. The languages that certain PDAs accept as an empty stack.

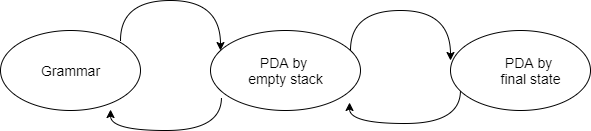
●      We've already established that (2) and (3) are identical.

●      It turns out that proving that (1) and (3) are the same is the simplest next step, implying that all three are equivalent.

Q7) Construct CFG to PDA?

A7) We can design a similar nondeterministic PDA that accepts the language produced by the context-free grammar G if it is context-free. For the grammar G, a parser can be created.

In addition, if P is a pushdown automaton, an analogous context-free grammar G can be built.

L(G) = L(P)

Algorithm to find PDA corresponding to a given CFG

Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)

Step1 - Convert the CFG's productions into GNF.

Step2 - There will be only one state q on the PDA.

Step3 - The CFG's start symbol will be the PDA's start sign.

Step4 - The PDA's stack symbols will be all of the CFG's non-terminals, and the PDA's input symbols will be all of the CFG's terminals.

Step5 - For each production in the form A → aX where a is terminal and A, X are a combination of terminal and non-terminals, make a transition δ (q, a, A).

Problem

Construct a PDA using the CFG below.

G = ({S, X}, {a, b}, P, S)

Where are the productions?

S → XS | ε , A → aXb | Ab | ab

Solution

Let's say you have a PDA that's equivalent to that.

P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)

Where δ −

δ(q, ε , S) = {(q, XS), (q, ε )}

δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}

δ(q, a, a) = {(q, ε )}

δ(q, 1, 1) = {(q, ε )}

Q8) Construct PDA to CFG?

A8) We can design a similar nondeterministic PDA that accepts the language produced by the context-free grammar G if it is context-free. For the grammar G, a parser can be created.

In addition, if P is a pushdown automaton, an analogous context-free grammar G can be built.

L(G) = L(P)

Algorithm to find CFG corresponding to a given PDA

Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F) such that the non- terminals of the grammar G will be {Xwx | w,x ∈ Q} and the start state will be Aq0,F.

Step1 − For every w, x, y, z ∈ Q, m ∈ S and a, b ∈ ∑, if δ (w, a, ε) contains (y, m) and (z, b, m) contains (x, ε), add the production rule Xwx → a Xyzb in grammar G.

Step2 − For every w, x, y, z ∈ Q, add the production rule Xwx → XwyXyx in grammar G.

Step3 − For w ∈ Q, add the production rule Xww → ε in grammar G.

Q9) Construct a PDA that accepts the language L over 0 and 1 by using an empty stack that accepts all strings of 0s and 1s where the number of 0s is twice the number of 1s.

A9) There are two parts to this PDA's design:

We'll start with the first portion, in which 1s occur before 0s. Read a single 1 and push two 1s onto the stack is the logic. After that, POP two 1s from the stack after reading two 0s. It's possible to δ

δ(q0, 1, Z) = (q0, 11, Z)        Here Z represents that stack is empty 

δ(q0, 0, 1) = (q0, ε) 

Consider the second portion, which is what happens if 0 arrives before 1's. The reasoning is to read the first 0 and place it on the stack, then change the state of q0 to q1. [Note that state q1 denotes that the first 0 has been read but the second 0 has not yet been read.]

If 1 is met while in q1, POP 0. If 0 is read while in q1, simply read the second 0 and go on. It δ will be as follows:

δ(q0, 0, Z) = (q1, 0Z) 

δ(q1, 0, 0) = (q1, 0) 

δ(q1, 0, Z) = (q0, ε)        (indicate that one 0 and one 1 is already read, so simply read the second 0) 

δ(q1, 1, 0) = (q1, ε) 

To summarize the PDA for the given L, it is as follows:

δ(q0, 1, Z) = (q0, 11Z) 

δ(q0, 0, 1) = (q1, ε) 

δ(q0, 0, Z) = (q1, 0Z) 

δ(q1, 0, 0) = (q1, 0) 

δ(q1, 0, Z) = (q0, ε) 

δ(q0, ε, Z) = (q0, ε)      ACCEPT state

Q10) Convert the following grammar to a PDA that accepts the same language.

1. S → 0S1 | A 
2. A → 1A0 | S | ε 

A10) The CFG can be first simplified by eliminating unit productions:

S → 0S1 | 1S0 | ε 

Now we will convert this CFG to GNF:

S → 0SX | 1SY | ε 

X → 1 

Y → 0 

The PDA can be:

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q11) Construct PDA for the given CFG, and test whether 0104 is acceptable by this PDA.

1. S → 0BB 
2. B → 0S | 1S | 0

A11) The PDA can be given as:

A = {(q), (0, 1), (S, B, 0, 1), δ, q, S, ?} 

The production rule δ can be:

R1: δ(q, ε, S) = {(q, 0BB)}

R2: δ(q, ε, B) = {(q, 0S) | (q, 1S) | (q, 0)}

R3: δ(q, 0, 0) = {(q, ε)}

R4: δ(q, 1, 1) = {(q, ε)}

Testing 0104 i.e., 010000 against PDA:

δ(q, 010000, S) ⊢ δ(q, 010000, 0BB) 

⊢ δ(q, 10000, BB)              R1 

⊢ δ(q, 10000,1SB)              R3   

⊢ δ(q, 0000, SB)               R2       

⊢ δ(q, 0000, 0BBB)             R1    

⊢ δ(q, 000, BBB)               R3       

⊢ δ(q, 000, 0BB)               R2     

⊢ δ(q, 00, BB)                 R3    

⊢ δ(q, 00, 0B)                 R2   

⊢ δ(q, 0, B)                   R3   

⊢ δ(q, 0, 0)                   R2 

⊢ δ(q, ε)                      R3   

ACCEPT 

Thus 0104 is accepted by the PDA.

Q12) Convert the given grammar to a PDA that accepts the same language.

1. S → 0S1 | A 
2. A → 1A0 | S | ε 

A12) To simplify the above grammar eliminating unit production in CFG:

S → 0S1 | 1S0 | ε

Here, we convert the CFG to GNF:

1. S → 0SX | 1SY | ε 
2. X → 1 
3. Y → 0 

The final PDA can be:

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}