Unit – 1
Introduction
Q1) Write the phases of compilation?
A1) Phases of compilation
The method of compilation includes the sequence of different stages. Each phase takes a source programme in one representation and produces output in another representation. From its previous stage, each process takes input.
The various stages of the compiler take place:
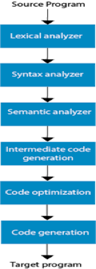
Fig: phases of compiler
Q2) Describe a compiler with its features?
A2) Compilers
● A compiler is a translator that translates the language at the highest level into the language of the computer.
● A developer writes high-level language and the processor can understand machine language.
● The compiler is used to display a programmer's errors.
● The main objective of the compiler is to modify the code written in one language without altering the program's meaning.
● When you run a programme that is written in the language of HLL programming, it runs in two parts.
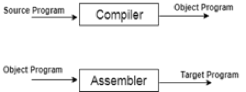
Fig: Execution process of Compiler
Features of compilers:
● Maintaining the right interpretation of the code
● The speed of the target code
● Understand prototypes for legal and illegal systems
● Good documentation / management of errors
● Correctness
● Speed of compilation
● Code debugging help
Q3) Write the task of the compilers?
A3) Task of compilers
Tasks which are performed by compilers:
● Divides the source programme into parts and imposes on them a grammatical structure.
● Allows you from the intermediate representation to construct the desired.
● target programme and also create the symbol table.
● Compiles and detects source code errors.
● Storage of all variables and codes is handled.
● Separate compilation support.
● Learn, interpret, and translate the entire programme to a semantically equivalent.
● Depending on the computer sort, conversion of the source code into object code.
Q4) Define DFA and NFA?
A4) DFA
DFA stands for Deterministic Finite Automata. Deterministic refers to computational uniqueness. In DFA, the character of the input goes to only one state. The DFA does not allow the null shift, which means that without an input character, the DFA does not change the state.
DFA has five tuples {Q, ∑, q0, F, δ}
Q: set of all states
∑: finite set of input symbol where δ: Q x ∑ →Q
q0: initial state
F: final state
δ: Transition function
NDFA
NDFA applies to Finite Non-Deterministic Automata. It is used for a single input to pass through any number of states. NDFA embraces the NULL step, indicating that without reading the symbols, it can change the state.
Like the DFA, NDFA also has five states. NDFA, however, has distinct transformation features.
NDFA's transition role may be described as:
δ: Q x ∑ →2Q
Q5) What is a regular expression?
A5) Regular Expression
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty
string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = {})
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular
● Expression denoting the language L(Y), then
● X + Y is a Regular Expression corresponding to the language L(X) ∪
L(Y) where L(X+Y) = L(X) ∪ L(Y).
● X. Y is a Regular Expression corresponding to the language L(X).
L(Y) where L (X.Y) = L(X). L(Y)
● R* is a Regular Expression corresponding to the language L(R*)
where L(R*) = (L(R)) *
● If we apply any of the rules several times from 1 to 5, they are Regular
Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by unix. These operators are used for
convenience only.
● character classes: ‘[‘<list of chars> ‘]’
● start of a line: ‘^’
● end of a line: ‘$’
● wildcard matching any character except newline: ‘.’
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
Q6) Explain regular language?
A6) Regular Language
A language is regular if, in terms of regular expression, it can be presented.
Regular expressions have the capability to express finite languages by defining a pattern for finite strings of symbols.
The grammar defined by regular expressions is known as regular grammar. The language defined by regular grammar is known as regular language.
Regular languages are closed under a wide variety of operations.
● Union and intersection
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection.
● Set complement
Pick a DFA recognizing the language, then swap the accept/non- accept markings on its states.
● String reversal
Pick an NFA recognizing the language. Create a new final state, with epsilon transitions to it from all the old final states. Then swap the final and start states and reverse all the transition arrows.
● Set difference
Rewrite set difference using a combination of intersection and set complement.
● Concatenation and Star
Pick an NFA recognizing the language and modify.
● Homomorphism
A homomorphism is a function from strings to strings. What makes it a homomorphism is that it’s output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w: w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So, h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For
example, 0 * 1 * is regular, but its subset {O n 1 n: n > = 0} is not regular, but its subset {01, 0011, 000111} is regular again.
Q7) Describe lexical analyzer generator?
A7) Lexical analyzer generator
Lex is a lexical analyzer generating programme. It is used to produce the YACC parser. A software that transforms an input stream into a sequence of tokens is the lexical analyzer. It reads the input stream and, by implementing the lexical analyzer in the C programme, produces the source code as output.
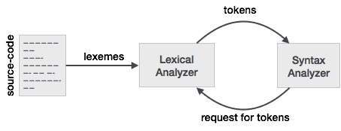
Fig: lexical analyzer generator
If a token is considered invalid by the lexical analyzer, it produces an error. The lexical analyzer works with the syntax analyzer in close collaboration. It reads character streams from the source code, checks for legal tokens, and, when necessary, passes the information to the syntax analyzer.
Tokens
It is said that lexemes are a character sequence (alphanumeric) in a token. For each lexeme to be identified as a valid token, there are some predefined rules. These rules, by means of a pattern, are described by grammar rules. A pattern describes what a token can be, and by means of regular expressions, these patterns are described.
Keywords, constants, identifiers, sequences, numbers, operators and punctuation symbols can be used as tokens in the programming language.
Example: the variable declaration line in the C language
int value = 100;
contains the tokens:
int (keyword), value (identifiers) = (operator), 100 (constant) and; (symbol)
Q8) What is role of parser?
A8) Role of a parser
The parser or syntactic analyzer obtains from the lexical analyzer a string of tokens and verifies that the grammar will produce the string for the source language. In the software, it reports any syntax errors. It also recovers from frequently occurring errors so that its input can continue to be processed.
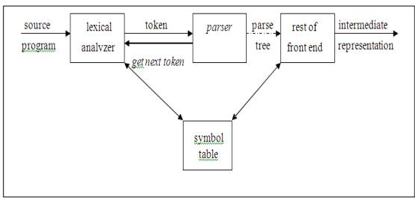
Fig: position of parser
Issues:
The parser is unable to detect errors like:
● Re-declaration of Variable
● Initialization of variable before use
● For an operation, data type mismatch.
The above problems are discussed in the Semantic Analysis stage.
Syntax Error Handling:
At several different levels, programmes can contain errors. For instance:
● Lexical, such as misspelling, keyword, or operator of an identifier.
● Syntactics, such as unbalanced parentheses in an arithmetic expression.
● Semantic, such as being applied to an incompatible operand by an operator.
● Logical, such as a call which is infinitely recursive.
Functions of error handler:
● It should clearly and reliably report the existence of errors.
● It should recover quickly enough from each mistake to be able to detect subsequent errors.
● The processing of right programmes does not substantially slow down.
Error recovery strategies:
The various methods a parse uses to recover from a syntactic error are:
The above topic described below:
Panic mode recovery
The parser discards input symbols one at a time upon finding an error before a synchronizing token is found. Typically, the synchronizing tokens are delimiters, such as end or semicolon. It has the value of simplicity and doesn't go through an endless loop. This approach is very useful when several errors in the same statement are uncommon.
Phase level recovery
The parser performs local correction on the remaining input when finding an error, which allows it to proceed. Example: Insert the missing semicolon, or erase the alien semicolon, etc.
Error production
The parser is constructed with error outputs using augmented grammar. If the parser uses error generation, suitable error diagnostics can be created to show the erroneous constructs that the input recognizes.
Global correction
Some algorithms can be used to find a parse tree for the y string because of the incorrect input string x and grammar G, such that the number of token insertions, deletions and changes is as limited as possible. In general, however, these methods are too expensive in terms of time and space.
Q9) Explain context-free grammar?
A9) Context free grammars
Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.
It consists of:
● a set of terminal symbols,
● a set of non-terminal symbols,
● a set of productions,
● a start symbol.
Context-free grammar G can be defined as:
G = (V, T, P, S)
Where
G - grammar, used for generate string,
V - final set of non-terminal symbol, which are denoted by capital letters,
T - final set of terminal symbols, which are denoted be small letters,
P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)
S - start symbol, which is used for derive the string
A CFG for Arithmetic Expressions -
An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:
1. <expression> --> number
2. <expression> --> (<expression>)
3.<expression> --> <expression> +<expression>
4. <expression> --> <expression> - <expression>
5. <expression> --> <expression> * <expression>
6. <expression> --> <expression> / <expression>
The only non-terminal symbol in this grammar is <expression>, which is also the
start symbol. The terminal symbols are {+, -, *, /, (,), number}
● The first rule states that an <expression> can be rewritten as a number.
● The second rule says that an <expression> enclosed in parentheses is also an <expression>
● The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.
Q10) Define context free language?
A10) Context free language
A context-free language (CFL) is a language developed by context-free grammar (CFG) in formal language theory. In programming languages, context-free languages have many applications, particularly most arithmetic expressions are created by context-free grammars.
A grammatical description of a language has four essential components -
● A variable that is being defined by the production. This variable is also called the production head.
● The production symbol ->
● A string of zero terminals and variables, or more.
Q11) Explain parse tree and derivation?
A11) Parse tree and Derivation
Derivation is a sequence of the laws of development. Via these production laws, it is used to get the input string. We have to make two decisions during parsing. That are like the following:
● The non-terminal that is to be replaced must be determined by us.
● We have to determine the law of development by which the non-terminal would be substituted.
We have two choices to determine which non-terminal is to be replaced by the rule of output.
Left most derivation:
The input is scanned and replaced with the development rule from left to right in the left-most derivation. In most derivatives on the left, the input string is read from left to right.
Example:
Production rules:
Input
a - b + c
The left-most derivation is:
S = S + S
S = S - S + S
S = a - S + S
S = a - b + S
S = a - b + c
Right most derivation:
The input is scanned and replaced with the development rule from right to left in the rightmost derivation. So, we read the input string from right to left in most derivatives on the right.
Example:
Input:
a - b + c
The right-most derivation is:
S = S - S
S = S - S + S
S = S - S + c
S = S - b + c
S = a - b + c
Parse Tree
● The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.
● In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.
● It is the symbol's graphical representation, which can be terminals or non-terminals.
● The parse tree follows operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.
Following these points, the parse tree:
● The terminals have to be all leaf nodes.
● Non-terminals have to be all interior nodes.
● In-order traversal supplies the initial string of inputs.
Example
Production rules:
Input
a * b + c
Step 1:
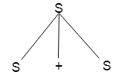
Step 2:
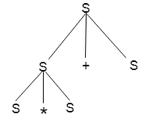
Step 3:
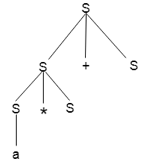
Step 4:
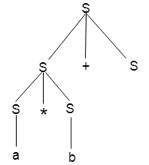
Step 5:

Q12) Write short notes on ambiguous grammar?
A12) Ambiguous grammar
A grammar is said to be ambiguous if there exists more than one leftmost derivation or more than one rightmost derivative or more than one parse tree for the given input string. If the grammar is not ambiguous then it is called unambiguous.
Example:
For the string aabb, the above grammar generates two parse trees:
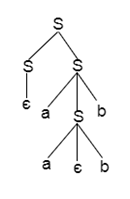
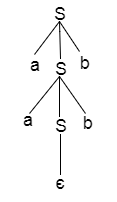
Fig: two parse trees
If the grammar has ambiguity, then it is not good for a compiler construction. No method can automatically detect and remove the ambiguity but you can remove ambiguity by re-writing the whole grammar without ambiguity.
Q13) Explain top down parsing?
A13) Top down parsing
Recursive or predictive parsing is known as top-down parsing.
The parsing begins with the start symbol in the top-down parsing and transforms it into the input symbol.
The top-down parser is the parser that, by expanding the non-terminals, generates a parse for the given input string with the aid of grammar productions, i.e., it begins from the start symbol and ends on the terminals.
Parse Tree The input string representation of acdb is as follows:
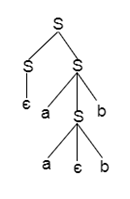
Fig: parse tree
There are 2 types of additional Top-down parser: Recursive descent parser, and non-recursive descent parser.
I. Recursive descent parser:
It is also known as Brute force parser or the with backtracking parser. Basically, by using brute force and backtracking, it produces the parse tree.
A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures.
The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking. But the related grammar (if not left-faced) does not prevent back-tracking. Predictive is considered a type of recursive-descent parsing that does not require any back-tracking.
As it uses context-free grammar that is recursive in nature, this parsing technique is called recursive.
II. Non-recursive descent parser:
It is also known with or without a backtracking parser or dynamic parser, LL (1) parser or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.
Q14) Describe LL (1) parsing?
A14) LL (1) parsing
It is also known with or without a backtracking parser or dynamic parser, LL (1) parser or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.
Predictive parser is a recursive descent parser, which has the capability to predict which production is to be used to replace the input string. The predictive parser does not suffer from backtracking.
To accomplish its tasks, the predictive parser uses a look-ahead pointer, which points to the next input symbols. To make the parser back-tracking free, the predictive parser puts some constraints on the grammar and accepts only a class of grammar known as LL(k) grammar.
Predictive parsing uses a stack and a parsing table to parse the input and generate a parse tree. Both the stack and the input contain an end symbol $ to denote that the stack is empty and the input is consumed. To make some decision on the input and stack element combination, the parser refers to the parsing table.
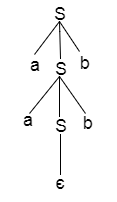
Fig: predictive parser
In recursive descent parsing, for a single instance of input, the parser can have more than one output to choose from, while in predictive parser, each stage has at most one production to choose from. There may be instances where the input string does not fit the production, making the parsing procedure fail.
Q15) Explain shift reduction parsing?
A15) Shift reduce parsing
● Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.
● Using a stack to hold the grammar and an input tape to hold the string, Shift reduces parsing.
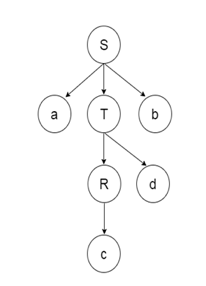
● The two acts are done by Shift Decrease Parsing: move and decrease. This is why it is considered that shift reduces parsing.
● The current symbol in the input string is moved into the stack for the shift operation.
● The symbols will be substituted by the non-terminals at each reduction. The mark is the right side of manufacturing and the left side of output is non-terminal.
Example:
Grammar:
Input string:
a1-(a2+a3)
Parsing table:
For bottom-up parsing, shift-reduce parsing uses two special steps. Such steps are referred to as shift-step and reduce-step.
Shift - step: The shift step refers to the progression to the next input symbol, which is called the shifted symbol, of the input pointer. Into the stack, this symbol is moved. The shifted symbol will be viewed as a single parse tree node.
Reduce - step: When a complete grammar rule (RHS) is found by the parser and substituted with (LHS), it is known as a reduction stage. This happens when a handle is located at the top of the stack. A POP function is performed on the stack that pops off the handle and substitutes it with a non-terminal LHS symbol to decrease.
Q16) Write about Parsing using Ambiguous grammars?
A16) Parsing using Ambiguous grammars
You may use the LR parser to parse ambiguous grammar. In the parsing table of ambiguous grammars, the LR parser resolves the conflicts (shift/reduce or decrease/reduce) based on certain grammar rules (precedence and/or associativity of operators).
Example:
Let's take the unclear grammar below:
E -> E+E
E -> E*E
E -> id
The precedence and associativity of the grammar operators (+ and *) can be considered to be as follows:
● “+” and “*” both are left associative,
● Precedence of “*” is higher than the precedence of “+”.
If we use LALR (1) parser, the LR (1) item DFA will be:
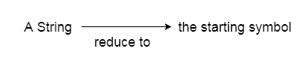
Fig: LR (1) item with DFA
We can see from the LR (1) DFA item that there are shift/reduce conflicts in the I5 and I6 states.
Fig: parsing table
"In I5 and I6, moves on "+ and "*" are both moved and decreased. To settle this dispute, we will use the precedence and associativeness of the operators to decide which phase to preserve and which to discard from the table.
Q17) Describe a parser generator?
A17) Parser generator
YACC is a program that generates the parser software automatically.
As we addressed YACC in the first unit of this course, you can go through the fundamentals again to make sure you understand everything.
YACC is an automatic tool which generates the programme for the parser.
YACC stands for Compiler Compiler Yet Another. The software is available under UNIX OS
LR parser construction requires a lot of work for the input string to be parsed.
Therefore, in order to achieve productivity in parsing and data, the procedure must provide automation.
Basically, YACC is an LALR parser generator that reports conflicts or uncertainties in the form of error messages (if at all present).
As we addressed YACC in the first unit of this tutorial, to make it more understandable, you can go through the concepts again.
● YACC
As shown in the picture, the standard YACC translator can be represented as
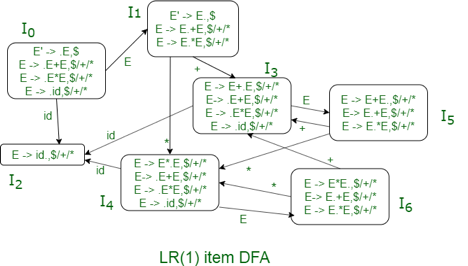
Fig: YACC automatic parser generator
Q18) Explain LR (1) parser?
A18) LR (1) parser
Different steps involved in LR (1) Parsing:
● Write context-free grammar for the specified input string.
● Verify the grammar's uncertainty.
● Add the Augmentation output to the specified grammar.
● Creating a canonical set of objects from LR (0).
● Drawing a diagram of data flow (DFA).
● Build a table for LR (1) parsing.
Augment Grammar:
If we add one more output to the given grammar G, Augmented Grammar G will be generated. It allows the parser to define when the parsing should be stopped and to announce the acceptance of the input.
Example
Given grammar
S → AA
A → aA | b
The Augment grammar G is represented by
Constructing canonical LR (1) parser
● Canonical lookahead is referred to by CLR. To create the CLR (1) parsing table, CLR parsing utilizes the canonical set of LR (1) objects. As compared to the SLR (1) parsing, the CLR (1) parsing table produces a greater number of states.
● We only position the reduction node in the lookahead symbols in the CLR (1).
● Different steps used in CLR (1) Parsing:
● Write a context free grammar for the specified input string
● Verify the grammar's uncertainty
● Add Increase output in the grammar specified
● Build a canonical set of things from LR (0)
● Drawing a diagram of data flow (DFA)
● Build a CLR (1) table for parsing
LR (1) item
Item LR (1) is a list of things from LR (0) and a look-ahead sign.
LR (1) item = LR (0) item + look ahead
The look ahead is used to decide where the final item will be put.
For the development of claims, the look ahead often adds the $ symbol.
Example
CLR (1) Grammar
Add Augment Production, insert the symbol '•' for each production in G at the first position and add the lookahead as well.
I0 state:
Add the output of Augment to the I0 State and compute the closure
I0 = Closure (S → •S)
In changed I0 State, add all productions beginning with S since "." is followed by the non-terminal. So, it will become the I0 State.
I0 = S → •S, $
S → •AA, $
In changed I0 State, add all productions beginning with A since "." is followed by the non-terminal. So, it will become the I0 State
I0= S → •S, $
S → •AA, $
A → •aA, a/b
A → •b, a/b
I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $
I2= Go to (I0, A) = closure (S → A•A, $)
"In I2 State, add all productions beginning with A since "." is followed by the non-terminal. The I2 Condition, then, becomes
I2= S → A•A, $
A → •aA, $
A → •b, $
I3= Go to (I0, a) = Closure (A → a•A, a/b)
In the I3 State, add all productions beginning with A since "." is followed by the non-terminal. The I3 Condition, then, becomes
I3= A → a•A, a/b
A → •aA, a/b
A → •b, a/b
Go to (I3, a) = Closure (A → a•A, a/b) = (same as I3)
Go to (I3, b) = Closure (A → b•, a/b) = (same as I4)
I4= Go to (I0, b) = closure (A → b•, a/b) = A → b•, a/b
I5= Go to (I2, A) = Closure (S → AA•, $) =S → AA•, $
I6= Go to (I2, a) = Closure (A → a•A, $)
"In I6 State, add all productions beginning with A since "." is followed by the non-terminal. The I6 Condition, then, becomes
I6 = A → a•A, $
A → •aA, $
A → •b, $
Go to (I6, a) = Closure (A → a•A, $) = (same as I6)
Go to (I6, b) = Closure (A → b•, $) = (same as I7)
I7= Go to (I2, b) = Closure (A → b•, $) = A → b•, $
I8= Go to (I3, A) = Closure (A → aA•, a/b) = A → aA•, a/b
I9= Go to (I6, A) = Closure (A → aA•, $) = A → aA•, $
Diagram DFA:
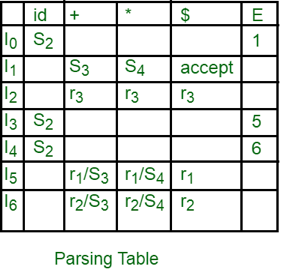
Fig: DFA
CLR (1) Parsing Table:

Productions are numbered according to the following:
The location of the move node in the CLR (1) parsing table is the same as the parsing table of the SLR (1).
Q19) Constructing LALR parser?
A19) LALR parser
The lookahead LR is alluded to by LALR. We use the canonical set of LR (1) objects to create the LALR (1) parsing table.
In the LALR (1) analysis, the LR (1) products that have the same outputs but look ahead differently are combined to form a single set of items
The parsing of LALR (1) is the same as the parsing of CLR (1), the only distinction in the parsing table.
LALR (1) Parsing:
LALR refers to the lookahead LR. To construct the LALR (1) parsing table, we use the canonical collection of LR (1) items.
In the LALR (1) parsing, the LR (1) items which have same productions but different look ahead is combined to form a single set of items
LALR (1) parsing is the same as the CLR (1) parsing, only difference in the parsing table.
Example
LALR (1) Grammar
Add Augment Production, insert the '•' symbol for each production in G at the first place and add the look ahead as well.
S → •S, $
S → •AA, $
A → •aA, a/b
A → •b, a/b
I0 State:
Add the output of Augment to the I0 State and measure Closure L
I0 = Closure (S → •S)
Add all productions beginning with S to I0 State, since the non-terminal is followed by '•'. The I0 Condition, then, becomes
I0 = S → •S, $
S → •AA, $
In changed I0 State, add all productions beginning with A since "•" is followed by the non-terminal. So, it will become the I0 State.
I0= S → •S, $
S → •AA, $
A → •aA, a/b
A → •b, a/b
I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $
I2= Go to (I0, A) = closure (S → A•A, $)
In the I2 State, add all productions beginning with A since "•" is followed by the non-terminal.
Q20) Describe SLR parsers and construction or SLR parsing tables?
A20) SLR parsers and construction or SLR parsing tables
Except for the decreased data, the SLR parser is similar to the LR (0) parser. Reduced outputs are written only in the FOLLOW of the variable whose output is reduced.
Construction of SLR parsing table: -
● If [A ->? A. .a? ] is set to 'move j' in Ii and GOTO(Ii, a) = Ij, then set ACTION[i, a]. A must-be terminal here.
● If [A ->? .] is in Ii and then ACTION[i, a] is set to "reduce A ->??" In FOLLOW(A) for all a '; here A may not be S'.
● Is [S -> S.] in Ii, then 'accept' is set to action [i, $].
3. For all nonterminal A, the goto transitions for state I are constructed using the rule:
if GOTO( Ii , A ) = Ij then GOTO [i, A] = j.
4. A mistake is made in all entries not specified by Rules 2 and 3.
If we have several entries in the parsing table, then it is said that a dispute is
Consider the grammar E -> T+E | T
T ->id
Augmented grammar - E’ -> E
E -> T+E | T
T -> id