Module 4

Electrical Machines

Q1) Explain the construction of transformer?

A1)

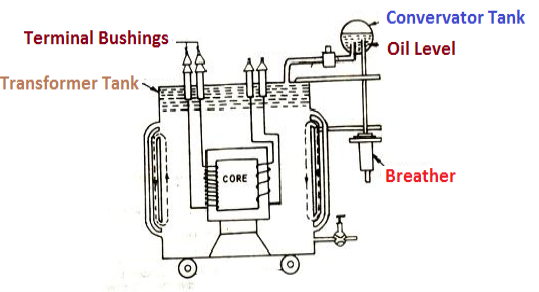
Material used for core is (silicon steel) it is used for its (high permeability) and (low magnetic reluctance) magnetic field produced is very strong

The core is formed of (stacks of laminated thin steel sheets) which are electrically isolated from each other.  They are typically (0.35 to 0.5 mm thick)

We can used 2 ‘L’ shaped sheets or 2 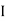 shaped sheets for laminations

Construction and types

L.V. = low voltage  H.V. = high voltage   are mounted on same limb to minimum leakage .

L.V. Winding placed inside and H.V. winding placed outside with (proper insulation between the winding as it is easy to insulated L.V. winding) than H.V. winding.

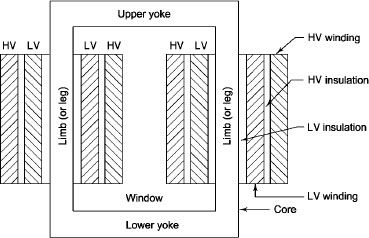
2.     Sandwiched

The H.V. and L.V. winding are divided into no. of small coils and there small windings are interleaved.

(the top and bottom winding are L.V. coils because they are close to core)

(To increase cooling surface are tubes or fins are provided)

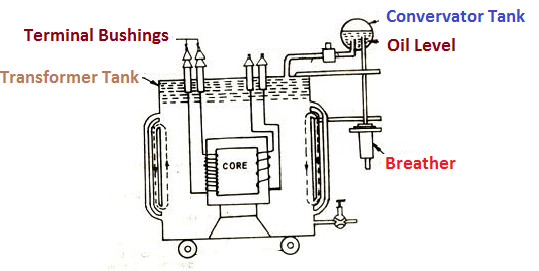
However during  contraction outside air can have moisture which will deteriorate the insulating properly of oil.

There is pipe connecting rain tank and conservator. On the pipe a protective device called Buccholz Relay is mounted.

When the Transformer is about to be faulty and draw range current the oil becomes very hot and decompose.

During this process different types of gases are liberated.(The Bucchoz Relay get operated by these gases) and gives an alarm to the operator. ɡȴ the fault continues to persist then there lay will trip off main circuit breaker to protect the Transformer.

An explosion Vent  or relief value is the bent up pipe filled on the main tank.

(The explosion vent consist of aluminium of oil ) when the T/F becomes faulty the cooling oil get decomposed and various types of gases are liberated

(ɡȴ the gas pressure exodus certain level then the aluminium of oil (diagram) in explosion vent will burst) to release pressure. The will save main tank from getting damaged.

Q2) Explain shell type transformer?

A2)

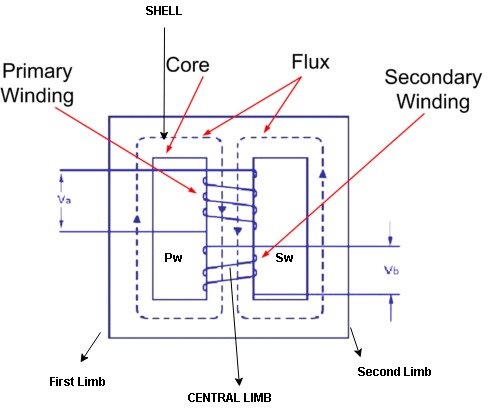
2 limbs

2.     single magnetic circuit    2. Double magnetic ckt.

3.     Winding encircles the core              3. Core encircles the winding

4.     One window                4. Two window

5.     Cylindrical type winding is used  5. Sandwich type is used

6.     Easy to repair                6. Not easy repair

7.     Preferred for Low voltage application  7. Preferred for high voltage application

8.     Provides better cooling since winding 8. Does not provide effective cooling as

Are uniformly distributed on 2 limbs     the winding are surrounding core.

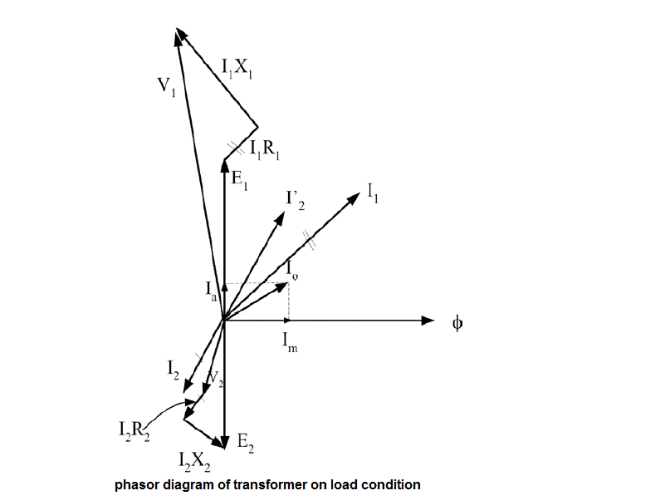
Q3) Explain the phasor diagram?

A3) When the transformer is connected to the AC source, an electrical current pass in the primary winding and this current called No load current (Io).

This current causes a production of variable magnetic flux.

This magnetic flux cuts both the primary and the secondary winding and generates in each of them an opposite Electro Motive Force (E.M.F) proportional to the number of turns and the rate of change in the flux of time. And the No load current is divided into two compounds Ia, Im

Ia:  is the cause of iron loss

Im:  is the cause of magnetizing circuit

Such that :

Ia = Io * cosφo

Im = Io * sinφo

Φo:  the angle between current Io and voltage for primary side

Power of transformer at no load condition:

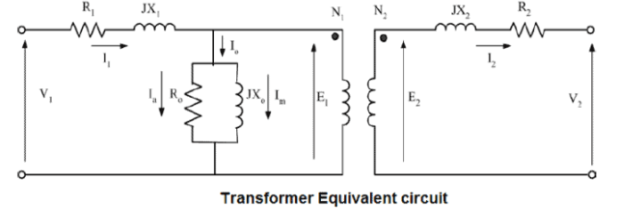
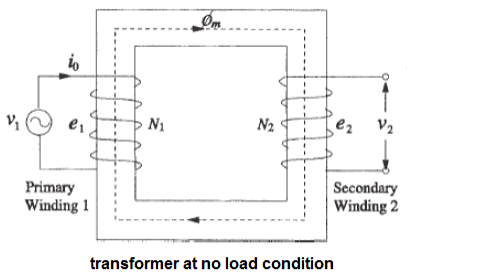
Because the primary winding has physical resistance (R1) and inductive reactance (X1), the current of the load causes a voltage drop at the terminals of the primary winding shown in the following relationship

= + *

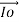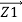
Z1 = [ R1 2 + X1 2] ½

At no load condition, the output power of transformer is equal to “Zero” and therefore the power withdrawn from the source (input power) is consumed in the loss of iron and copper So, we can neglect the losses of copper because of the small primary current and the absence of current in the secondary.

Po = V1 * Io * cosφo

This iron loss is consumed in the resistance of the magnetic circuit Ro and shown at the following relationship :

Ro = (V1/ Ia) = (V1/ Io * cosφo)

Also we can calculate reactance Xo from following relationship :

Xo = (V1/ Im) = (V1/ Io * sinφo)

So, We notice that the current (Io) is passed in the case of  “on load ” or “without load” and also the iron loss is fixed as long as the transformer is connected to the rated operating voltage.

How to draw phasor diagram of transformer at no load condition:

If we assume that the voltage wave V1 is a sine wave, the current (Im) causing the magnetic flux is 90 degrees lagging and therefore the flux is also lagging at the same angle due to the flow of current in the inductive reactance

So,

= + *

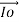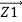
Z1 = [ R1 2 + X1 2] ½

Phasor diagram of transformer on load condition:

When a load is connected to the terminals of the secondary winding (Z2) , an electrical current passes in secondary side called the secondary winding current (I2) due to the impedance of the load. This current causes a magnetic flux  in the iron core. this value of magnetic flux depends on the current of I2 So, This flux must be opposite by another counter flux in the primary winding.

So, at loading condition the total current of the load (I2), I2 = (V2/Z2) is the total current which drawn by the load from the source so we can represent the phasor diagram of transformer as follows :

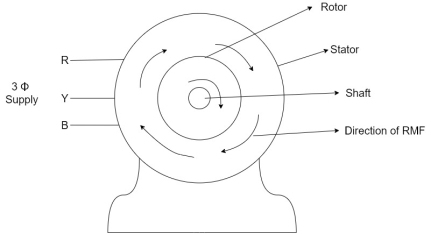
Q4) Explain the basic principle of three phase induction motor?

A4) Principle of operation of induction motor:

Q5) Explain the torque equation of induction motor?

A5) Torque produced in induction motor depends upon the following factors

1.The rotor power factors ( CosФ) under running condition

2.The rotor current under running condition

We can mathematically say that,

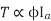,    As per DC (M) equation

  But in case of induction motor

Suffix 1 -> used for stator/stator parts (qty)

Suffix 2-> used for rotor/rotor parts(qty)

Therefore,    ----(1)

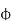= flux that induces the EMF in rotor

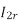= rotor current under running condition

= P.F of rotor

But,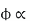stator vtg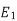also i.e

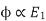----(2)

Transformation ratio i.e. given by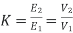

Therefore, 

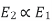and hence

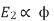also

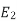at slip ’S’ is given by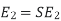

And also at slip ‘S’ i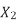s =S.

Hence 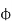in equation can be replaced by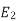 

i.e. 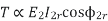U

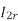= ----(3)----()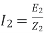

4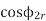 = 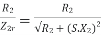  ------(4)

Substract (3) and (4) into (1) equation we get,

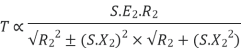
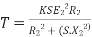(N-m) , Torque equation of I.M.

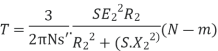
At starting condition slip S=1

So,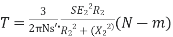

Q6) Explain rotating magnetic field ?

A6) Rotating magnetic field is magnetic field which rotates in space about some point or axis. The North and South poles continuously rotates with a specific speed, called synchronous speed.  All poly phase electrical machines are associated with rotating magnetic field in the air gap. Therefore, an understanding of rotating magnetic field produced by poly phase winding is very important to analyze and understand the principle and operation of electrical machine viz. Synchronous Machine and Induction Machine.

Condition for Generation of Rotating Magnetic Field

When a balanced poly phase current flows in the balanced poly phase winding, a rotating magnetic field is produced. The necessary condition for generation of rotating magnetic field is that “the time angle displacement between the currents and space angle displacement between the winding axes must be equal.”

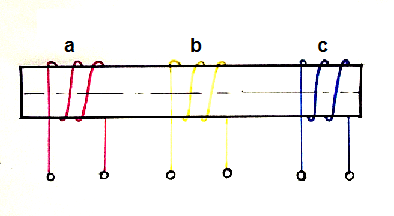
Let us consider an example for better understanding of the above mentioned condition. In the figure below, three coils a, b and c with their magnetic axis coincident are excited by three phase balanced current Imsinωt, Imsin(ωt-120°) and Imsin(ωt+120°).

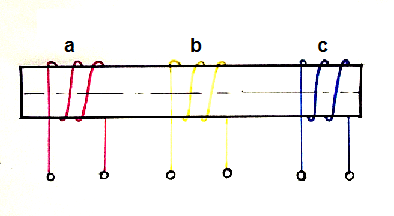
In this case, the time angle displacement between the currents is 120 degree but the space angle displacement between the winding axes zero. Therefore, rotating magnetic field will not be produced.

Q7)Explain the phasor diagram of rotating magnetic field?

A7) Two Conditions for production of Rotating Magnetic field :

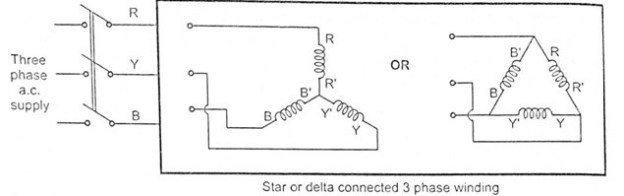
The three phase currents flow simultaneously through the windings and are displaced from each other by 120 degree electrical. Each alternating phase current produces its own flux which is sinusoidal. So all three fluxes are sinusoidal and are separated from each other by 120 degree. If the phase sequence of the windings is R-Y-B, then mathematical equations for the instantaneous values of the three fluxes ΦR, ΦB, ΦY can be written as, (The flux ΦR is taken as reference phasor) :

ΦR = Φm sin (ωt) = Φm sin θ

ΦY = Φm sin (ωt – 120∘) = Φm sin( θ – 120∘)

ΦB = Φm sin (ωt – 240∘) = Φm sin( θ – 240∘)

As windings are identical and supply is balanced, the magnitude of each flux is . Due to phase sequence R-Y-B, flux ΦY lags behind ΦR by 120 degree and ΦB  lags ΦY by 120 degree. So ΦB ultimately lags ΦR by 240 degree.

 ΦR = Φm sin(0∘) = 0

ΦY = Φm sin(-120∘) = – 0.866 Φm

ΦB =  Φm sin(-240∘) = + 0.866 Φm

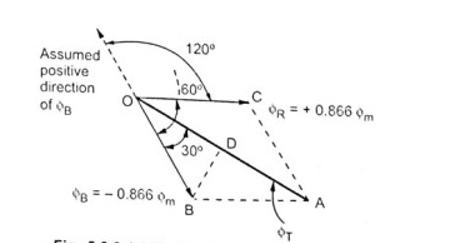
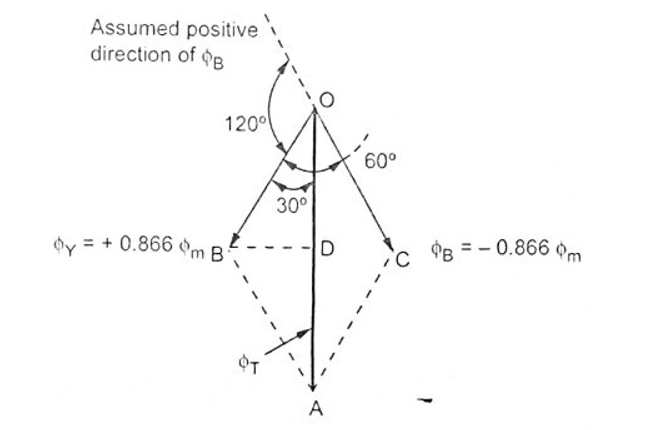
The phasor addition is shown in the figure. BD is drawn perpendicular from B on ΦT. It bisects ΦT.

OD = DA = ΦT  / 2

In triangle OBD, angle BOD = 30∘

cos(30∘) = OD / OB = (ΦT  / 2) / 0.866Φm

⇒ ΦT = 2 × 0.866 Φm × cos(30∘) = 1.5 Φm 

So magnitude of ΦT is 1.5 Φm  and its position is vertically upwards at θ = 0∘.

ΦR = Φm sin(60∘) = + 0.866 Φm

ΦY = Φm sin(-60∘) = – 0.866 Φm

ΦB =  Φm sin(-180∘) = 0

So ΦR is positive and ΦY  is negative and hence drawing in appropriate directions we phasor diagram as shown in figure.

Doing the same construction, drawing perpendicular from B on ΦT at D we get the same results.

ΦT = 1.5 Φm

But it can be seen that though its magnitude is 1.5 Φm it has rotated through 60∘ in space, in clockwise direction, from its previous position. 

ΦR = Φm sin(120∘) = + 0.866 Φm

ΦY = Φm sin(0∘) = 0

ΦB =  Φm sin(-120∘) = – 0.866 Φm

After doing the same construction as before it can be proved again that,

ΦT = 1.5 Φm

But it can be seen that though its magnitude is 1.5 Φm it has rotated through 120∘ in space, in clockwise direction, from its 1st position θ = 0∘. 

ΦR = Φm sin(180∘) = 0

ΦY = Φm sin(60∘) = + 0.866 Φm

ΦB =  Φm sin(-160∘) = – 0.866 Φm

Magnitude of net flux remains same, if further rotated through 60∘ from its previous position in clockwise direction.

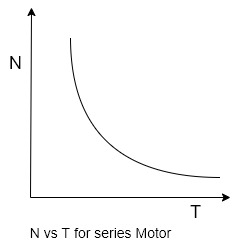
Q8) Explain the torque speed characteristics of DC machine?

A8) Speed torque characteristics

These characteristics can be derived from above two characteristics

Motor characteristics

This graph is similar to speed armature current characteristics as torque is proportional to the armature current this curve shows that the speed almost remains constant torque changes from no load to full load conditions.

Characteristics of DC series motor

For the series motor the series field winding is carrying the entire armature current hence,

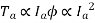
The torque in case of series motor is proportional to the square of the armature current this relation is parabolic in nature as shown in the figure

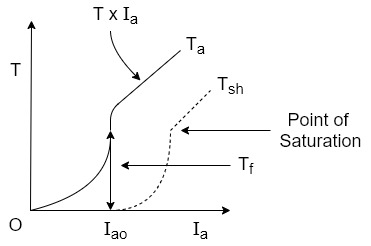
As load increases armature current increases and torque produced increases proportional to the square of the armature current upto a certain limit.

As the entire current passes through the series field there is a property of an electromagnet called saturation may occur.

Saturation means though the current through the winding increases the flux produced remains constant hands after saturation the characteristics take the shape of straight line is flux becomes constant as shown.

The difference between is loss torque . shown in figure

Speed armature current characteristics

From the speed equation we get

As in case of series motor

The values of 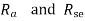   are so small that the effect of change in 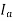on the speed overrides effect of change in  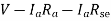on the speed . Hence in the speed equation  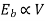and can be assumed constant

So speed equation reduces to

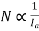
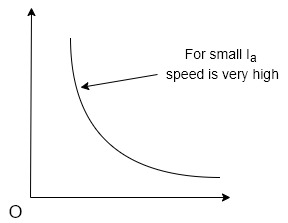
Speed armature current characteristics is rectangular hyperbola type as shown in figure

Speed torque characteristics

In case of series motors

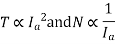
Hence we can write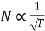

Thus as torque increases when load increases the speed decreases.

On no load torque is very less and hence speed increases to dangerously high value.

Thus the nature of the speed torque characteristics is similar to the nature of the speed armature current characteristics.

Speed control of DC shunt motor

The set of for speed control of DC shunt motor using the flux control technique is shown in figure.

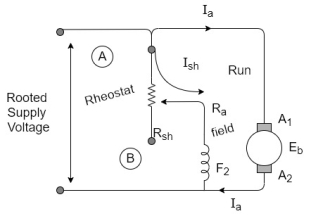
In order to change speed we have to change flux this can be achieved by changing the field current the field current can be changed by changing the value of rheostat R, connected in series with the field winding as shown in figure

See at the time of starting we need to run the motor slowly that means the clock should be maximum because

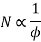
To obtain maximum Flux the field current should be maximum for this the value of rheostat(R) should be maximum.

Hence at the time of starting the variable point at rheostat is kept at point A and figure (a)

A rated constant supply voltage is applied to the set up so aerated field current will flow.

Hence a rated flux is produced which ultimately result in a rated speed of the motor.

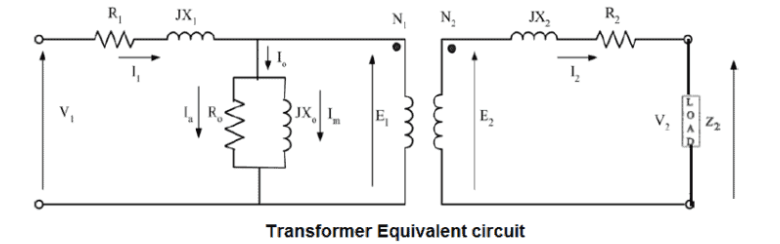
Q9) Explain the EMF equation?

A9)

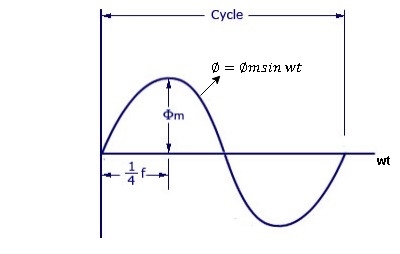
As primary winding excited by the a sinusoidal alternating voltage an alternating current flows in the winding producing an alternating varying flux Ø

Ø = Øm sin wt

As per Faradays Law of Electromagnetic Induction emf E1 is induced

E1 = N1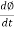 

E1 = N1 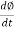   (Ø Sin wt)

= -  N1  Øm w  Cos wt

                       Sin (90-wt)

= - Sin (wt-90)

E1 = N1 Øm   w Sin (wt-90)

w =

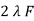
E1 = 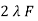N1 Ø m Sin (wt-90)

Max value of E1 = E max

Is when Sin (wt-90) = 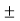1

E1 max = 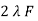N1 Ø m

Hence rms value of induced EMF in primary winding

E1 rms =   =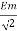  

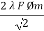
E1 = 4.44 F Ø m N1

Similarly RMS value of induced EMF in secondary wdg Is

E2 = 4.44 F Ø m N2

Q10) What are the methods of DC excitation?

A10) There are three methods of excitation, and thus three main types of DC generators:

Separately Excited DC Generator

These are the generators whose field magnets are energized by some external DC source, such as a battery.

A circuit diagram of separately excited DC generator is shown in the figure below. The symbols below are:

Voltage drop in the armature = Ia × Ra (R/sub>a is the armature resistance)

Let,

Ia = IL = I

Then,

Voltage across the load V = I Ra

Power generated is equal to

Pg = Eg X I

And power delivered to the external load is equal to

PL = V x I

Self Excited DC Generators

Self-excited DC generators are generators whose field magnets are energized by the current supplied by themselves. In these type of machines, field coils are internally connected with the armature.

Due to residual magnetism, some flux is always present in the poles. When the armature is rotated, some EMF is induced. Hence some induced current is produced. This small current flows through the field coil as well as the load and thereby strengthening the pole flux.

As the pole flux strengthened, it will produce more armature EMF, which cause the further increase of current through the field. This increased field current further raises armature EMF, and this cumulative phenomenon continues until the excitation reaches the rated value.

According to the position of the field coils,self excited DC generator may be classified as:

Series Wound Generator

In these type of generators, the field windings are connected in series with armature conductors, as shown in the figure below.

Whole current flows through the field coils as well as the load. As series field winding carries full load current it is designed with relatively few turns of thick wire. The electrical resistance of series field winding is therefore very low (nearly 0.5Ω ).

Here:

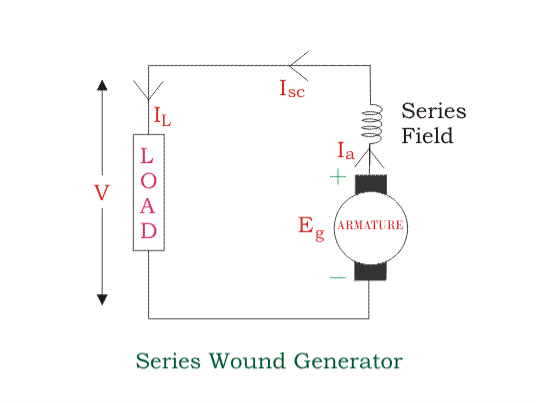
Then,

Ia = Isc = IL = I

Voltage across the load is equal to,

V = Eg – I (Ia x Ra)

Power generated is equal to,

Pg = Eg x I

Power delivered to the load is equal to,

PL = V x I

Shunt Wound DC Generators

In these type of DC generators, the field windings are connected in parallel with armature conductors, as shown in the figure below. In shunt wound generators the voltage in the field winding is same as the voltage across the terminal.

Here:

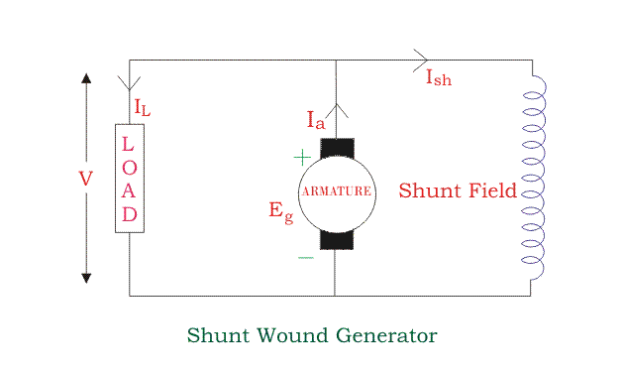
Here armature current Ia is dividing in two parts – one is shunt field current Ish, and another is load current IL.

So,

Ia = Ish + IL

The effective power across the load will be maximum when IL will be maximum. So, it is required to keep shunt field current as small as possible. For this purpose the resistance of the shunt field winding generally kept high (100 Ω) and large no of turns are used for the desired EMF.

Shunt field current is equal to,

Ish = V/ Rsh

Voltage across the load is equal to,

V = Eg – Ia Ra

Power generated is equal to,

Pg = Eg x Ia

Power delivered to the load is equal to,

PL = V x IL