MODULE-3

Linear differential equation

Question-1: Solve (4D² +4D -3)y =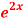 

Solution: Auxiliary equation is 4m² +4m – 3 = 0

    We get,             (2m+3)(2m – 1) = 0

                               m =   ,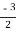

Complementary function:  CF is  A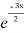+ B

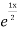
Now we will find particular integral,

                         P.I. = 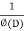f(x)

=   .

=    .

=    .

=   . =   .

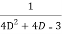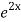
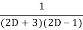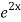
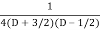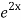
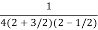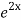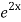
General solution is y =  CF + PI

                                                    = A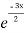+ B  .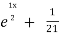

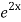
Question-2: Solve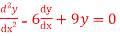

Or,

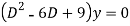
Ans. Auxiliary equation is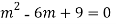

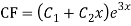
Question-3: Solve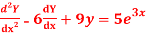

Ans. Given,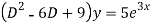

Auxiliary equation is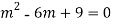

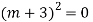
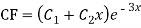
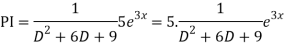
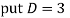
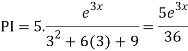
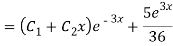
Question-4: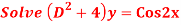

Ans. Auxiliary equation are

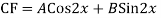
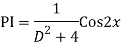
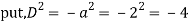
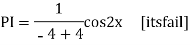
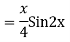
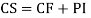
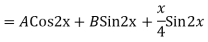
Question-5: Solve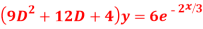

Ans. The AE is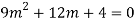

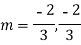
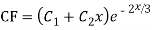
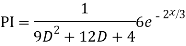
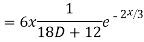
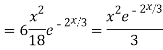
Complete solution y= CF + PI

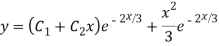
Question-6: Solve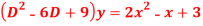

Ans. The AE is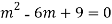

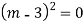
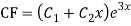
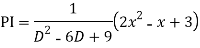
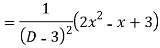
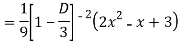
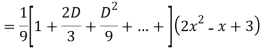
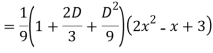
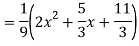
Complete solutio0n is y= CF + PI

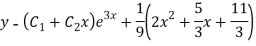
Question-7: solve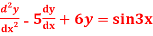

Ans. Given equation in symbolic form is

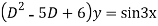
Its Auxiliary equation is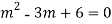

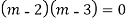
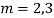
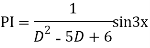
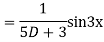
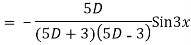
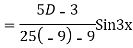
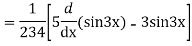
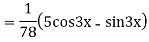
Complete solution is y= CF + PI

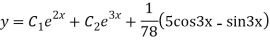
Question-8: Solve(D3-7D-6) y=e2x (1+x)

Ans. The auxiliary equation i9s

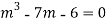
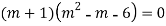
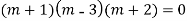
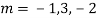
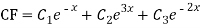
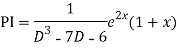
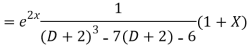
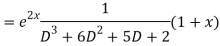
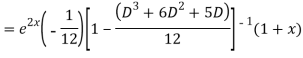
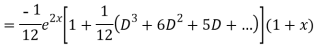
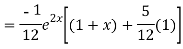
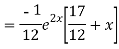
Hence complete solution is y= CF + PI

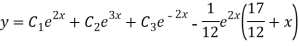
Question-9: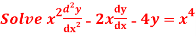

Ans. Putting,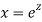

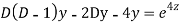
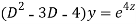
AE is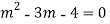

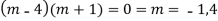
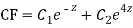
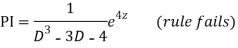
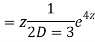
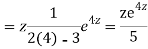
CS = CF + PI

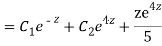
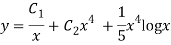
Question-10: solve – y = 2x² - x – 3

Solution.: first we find general solution:

    The characteristic function is:   r² - 1 = 0

( r-1)(r+1) = 0

                                                           R = 1, -1

General solution is -  A + B,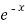

Now , let        

                                              y = ax² + bx +c

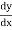  = 2ax + b

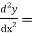2a

Put these value in  – y = 2x² - x – 3,

                           2a – (ax² + bx +c) = 2x² - x – 3

                           2a – ax² - bx - c = 2x² - x – 3

Now compare coeff.

Coeff. Of x² ,    a = -2

Coeff. Of x ,      b = 1

Constant coeff.

                                 2a – c = -3,       c =-1

So the particular solution will be,

             y =  -2x² + x – 1

Complete solution is,

              y = A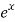 + B- 2x² + x – 1

Question-11: Solve the following by using the method of variation of parameters.

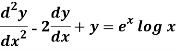
Sol. This can be written as-

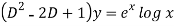
C.F.-

Auxiliary equation is-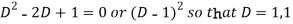

So that the C.F. Will be-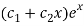

P.I.-

Here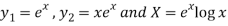

Now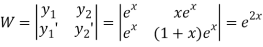

Thus PI = 

            = 

            = 

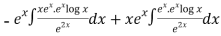
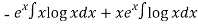
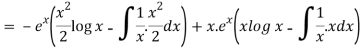
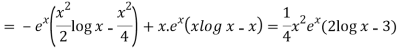
So that the complete solution is-

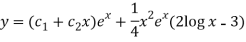
Question-12: Resistors of R1= 10Ω, R2 = 4Ω and  R3 = 8Ω are connected up to two batteries (of negligible resistance) as shown. Find the current through each resistor.

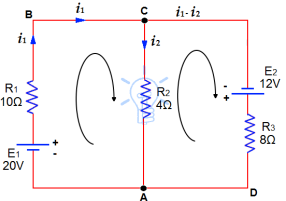
Solution:

Assume currents to flow in directions indicated by arrows

Apply KCL on junctions C and A

Therefore, current in mesh ABC = i1

Current in Mesh CA = i2

Then current in mesh is = i1-  i2

Now, apply KVL on mesh ABC,20V are acting in clockwise direction,equating the sum of IR products, we get

10i1 +4i2 = 20.....(1)

In mesh ACD 12 volts are acting in clock-wise direction, then

8( i1 -  i2)-4i2 = 12

8 i1 - 8 i2-4i2 = 12

8 i1 - 12 i2 = 12...(2)

Multiplying eq(1) by 3 we get

30 i1 + 12 i2 = 60

By solving equation 1 and 2 we get,

38i1 = 72

The above equation can be also simplified by elimination or cramer’s ruke

  I1 = 72/38 = 1.895 Amperes = current in 10 ohms resistor

Substituting this value in (1) we get,

10(1.895)+4i2 = 20

4i2 = 20-18.95

I2 = 0.263 Amperes=current in 4 ohms resistors

Now ,

i1-  i2 = 1.895-0.263=1.632 Amperes