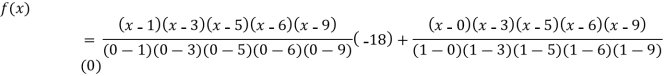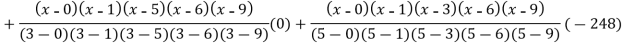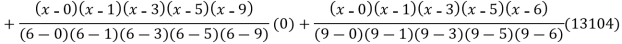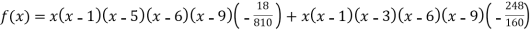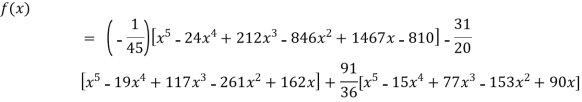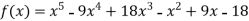Unit - 1
Solution of non-linear, linear equations and interpolation
Q1) Define algebraic and transcendental equations with examples.
A1)
There are two types of equations Linear and Non-linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 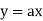 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
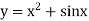 is a non-linear equation.
is a non-linear equation.

Algebraic Equation:
If f(x) is a pure polynomial, then the equation 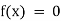 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 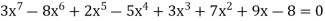
Transcendental Equation:
If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 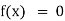 is called transcendental equation.
is called transcendental equation.
Ex 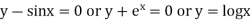
Q2) What do you understand by bisection method?
A2)
Bisection method consists of finding the root of the equation 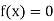 which lies between a and b (say).
which lies between a and b (say).
The function 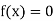 is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
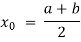
If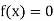 , then the correct root is
, then the correct root is  .But if
.But if , then the root either lies between a and
, then the root either lies between a and 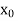 or
or  and b according as
and b according as 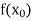 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
Q3) State the Newton-Raphson formula.
A3)
Let 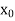 be the approximate root of the equation
be the approximate root of the equation .
.
By Newton Raphson formula 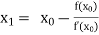
In general, 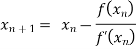
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Q4) Find a real root of 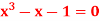 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
A4)
Let 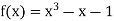 then by hit and trial we have
then by hit and trial we have
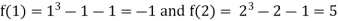
Thus 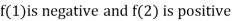 .So the root of the given equation should lies between 1 and 2.
.So the root of the given equation should lies between 1 and 2.
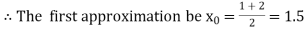
Now, 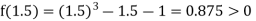
i.e., positive so the root of the given equation must lie between 

Now, 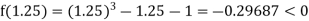
i.e., negative so the root of the given equation lies between 
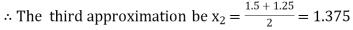
Now, 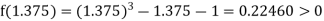
i.e., positive so the root of the given equation lies between 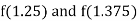
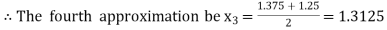
Now, 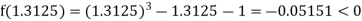
i.e., negative so that the root of the given equation lies between 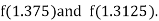
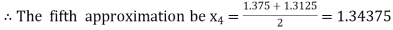
Now, 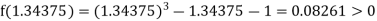
i.e., positive so that the root of the given equation lies between 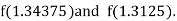
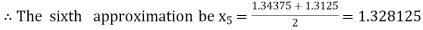
Now, 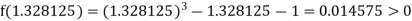
i.e., positive so that the root of the given equation lies between 
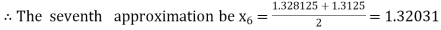
Now, 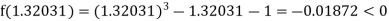
I.e. negative so that the root of the given equation lies between 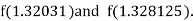

Now, 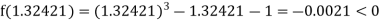
i.e., negative so that the root of the given equation lies between 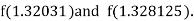
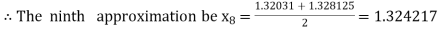
Hence the approximate root of the given equation is 1.32421
Q5) Find the root of the equation 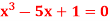 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
A5)
Let 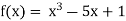
Where 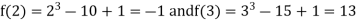
Thus 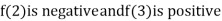 .So the root of the given equation should lies between 2 and 3.
.So the root of the given equation should lies between 2 and 3.

Now, 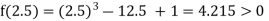
i.e., positive so the root of the given equation must lie between 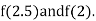

Now, 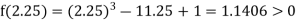
i.e., positive so the root of the given equation must lie between 

Now, 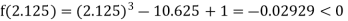
i.e., negative so the root of the given equation must lie between 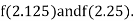
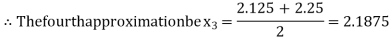
Now, 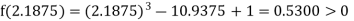
i.e., positive so the root of the given equation must lie between 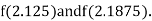
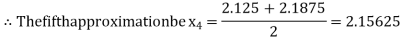
Now, 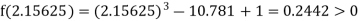
i.e., positive so the root of the given equation must lie between 
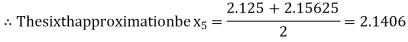
Now, 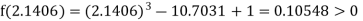
i.e., positive so the root of the given equation must lie between 
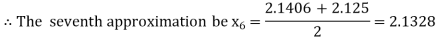
Now, 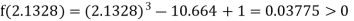
i.e., positive so the root of the given equation must lie between 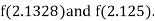
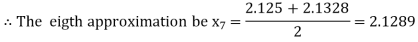
Now, 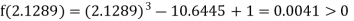
i.e., positive so the root of the given equation must lie between 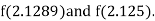
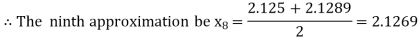
Hence the root of the given equation correct to two decimal place is 2.1269
Q6) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places)  near to 4.5
near to 4.5
A6)
Let 

The initial approximation 
By Newton Raphson Method

For n =0, the first approximation 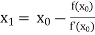
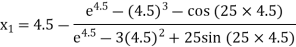
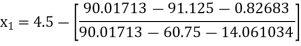
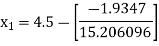
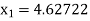
For n =1, the second approximation 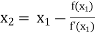
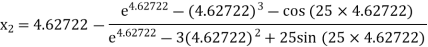

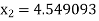
For n =2, the third approximation 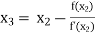
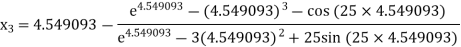
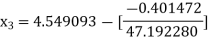
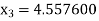
For n =3, the fourth approximation 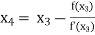
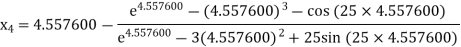
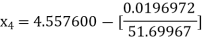
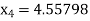
Hence the root of the equation correct to three decimal places is 4.5579
Q7) Find the real root of the equation 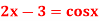
A7)
Correct to three decimal places in the interval 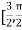 ]
]
The given equation is 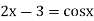 ... (1)
... (1)

Or 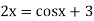
Or  =
=  ... (2)
... (2)
Or 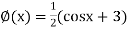
Let 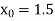 , in the interval
, in the interval 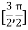 .
.
The successive approximation we have

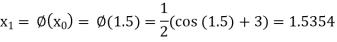
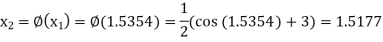
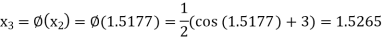
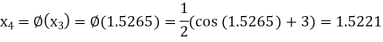

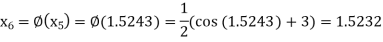

Hence the root of the equation correct to three decimal places is 1.524.
Q8) By iteration method, find the value of 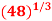 , correct to three decimal places.
, correct to three decimal places.
A8)
Let 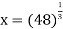

Let  .
.
Also 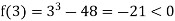

Therefore the root of the equation lies between 3 and 4.
Given equation can rewrite 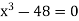 .
.


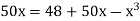
Or  … (2)
… (2)
Let  , in the interval
, in the interval 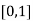 .
.
The successive approximation we have
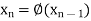
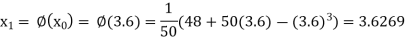
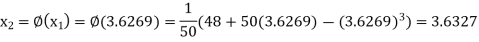
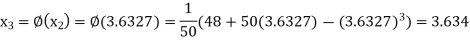
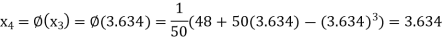
Hence the root of the equation correct to three decimal places is 3.634.
Q9) State the Jacobi iteration method.
A9)
Let us consider the system of simultaneous linear equation
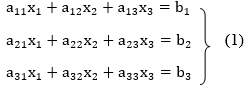
The coefficients of the diagonal elements are larger than the all-other coefficients and are non-zero. Rewrite the above equation we get
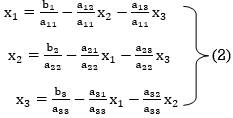
Take the initial approximation 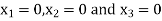 we get the values of the first approximation of
we get the values of the first approximation of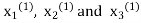 .
.
By the successive iteration we will get the desired the result.
Q10) Use Gauss –Seidel Iteration method to solve the system of equations 
A10)
Since 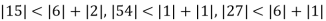
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations

Let the initial approximation be 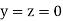
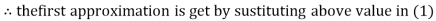
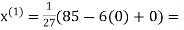 3.14814
3.14814
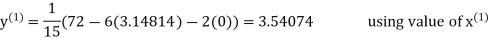

 2.43217
2.43217
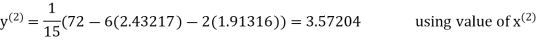
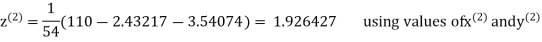
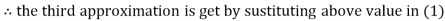
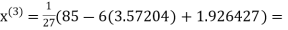 2.42571
2.42571
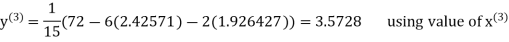
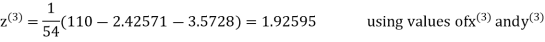
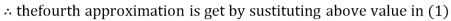
 2.4260
2.4260
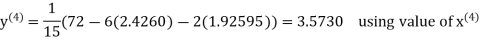

Hence the solution correct to three decimal places is

Q11) Solve the following equations by Gauss-Seidel Method
A11)



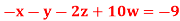
A11)
Rewrite the above system of equations
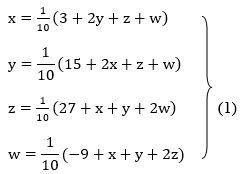
Let the initial approximation be 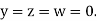

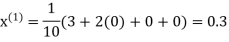
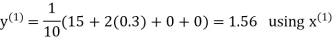




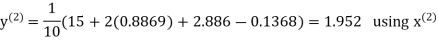
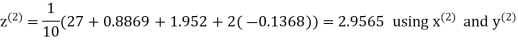
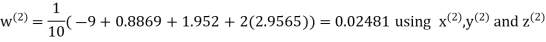


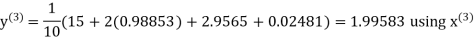
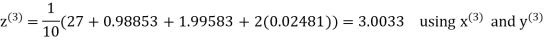
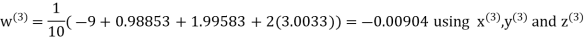

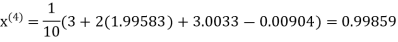
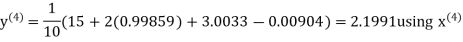
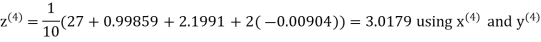
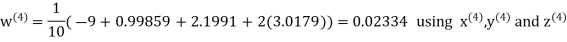


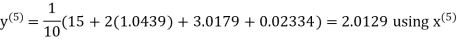
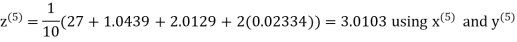
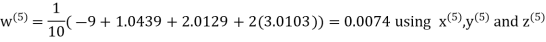
Hence the required solution is 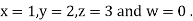
Q12) Solve the equations-
A12)
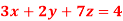

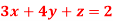
A12)
Let

So that-

3. 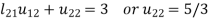
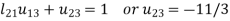
4. 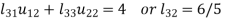
5. 
So

Thus-
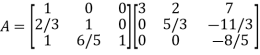
Writing UX = V,
The system of given equations become-
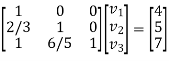
By solving this-
We get-
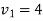
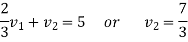
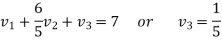
Therefore the given system becomes-
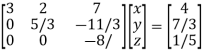
Which means-
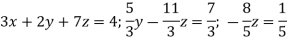
By back substitution, we get the values of x, y and z
Q13) State Cholesky method.
A13)
Consider a system of equations
AX = B … (1)
If the coefficient matrix A is symmetric and positive definite then A can be decomposed as
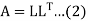
Where L is a lower triangular matrix.
A may also be decomposed as 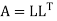 where U is an upper triangular matrix.
where U is an upper triangular matrix.
From (1) and (2),

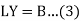
Where
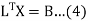
The values 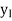 , 1
, 1 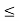 i
i 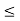 n can be obtained by forward substitution and the solution
n can be obtained by forward substitution and the solution 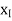 ,,1
,,1  i
i  n is obtained by back substitution.
n is obtained by back substitution.
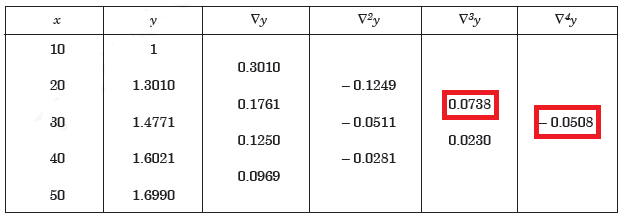
Q14) Construct a backward difference table for y = log x, given-
A14)
X | 10 | 20 | 30 | 40 | 50 |
y | 1 | 1.3010 | 1.4771 | 1.6021 | 1.6990 |
A14)
The backward difference table will be-
Q15) Given  find
find  , by using Newton forward interpolation method.
, by using Newton forward interpolation method.
A15)
Let 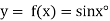 , then
, then
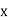 | 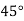 |  | 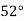 | 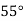 | 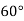 |
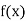 | 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
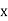 | 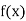 |  | 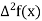 | 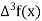 |
45 50 55 60 | 0.7071 0.7660 0.8192 0.8660 | 0.0589 0.0532 0.0468 | -0.0057 -0.0064 | -0.0007 |
By Newton forward difference method
Here initial value 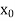 = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.

By Formula
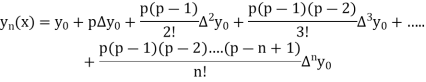
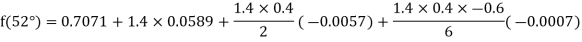
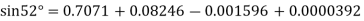
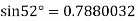
Q16) Find 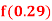 from the following table)
from the following table)
A16)
 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
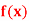 | 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
A16)
Consider the backward difference method
 | 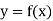 | 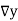 |  | 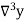 | 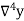 | 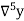 |
0.20 0.22 0.24 0.26 0.28 0.30 | 1.6596 1.6698 1.6804 1.6912 1.7024 1.7139 | 0.0102 0.0106 0.0108 0.0112 0.0115 | 0.0004 0.0002 0.0004 0.0003 | -0.0002 0.0002 -0.0001 | 0.0004 -0.0003 | -0.0007 |
Here 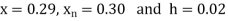
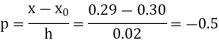
By Newton backward difference formula
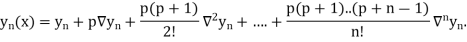
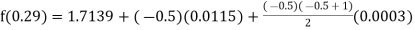
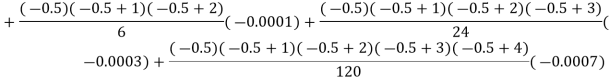


Q17) y means of Newton’s divided difference formula, find the values of  from the following table)
from the following table)
A17)
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
A17)
We construct the divided difference table is given by:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference | Fourth order divide difference |
4 5 7 10 11 13 | 48 100 294 900 1210 2028 | 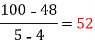 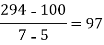 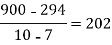 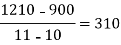 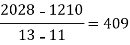 | 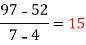 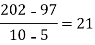 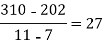  | 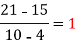 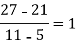 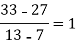 | 0 0 |
By Newton’s Divided difference formula
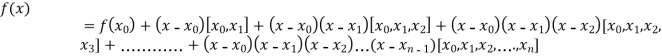 .
.
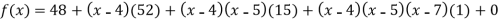
Now, putting 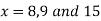 in above we get
in above we get
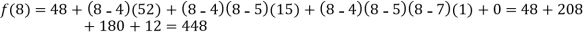 .
.
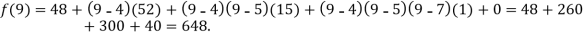
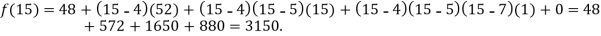
Q18) Find a polynomial satisfied by 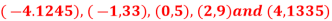 , by the use of Newton’s interpolation formula with divided difference.
, by the use of Newton’s interpolation formula with divided difference.
A18)
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
We will construct the divided difference table:
x | F(x) | First order divided difference | Second order divided difference | Third order divided difference | Fourth order divided difference |
-4 -1 0 2 4 | 1245 33 5 9 1335 | 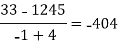 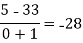 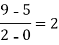 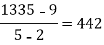 | 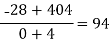 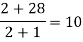 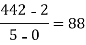 | 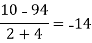  | 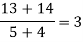 |
By Newton’s divided difference formula
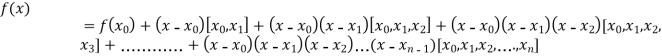 .
.
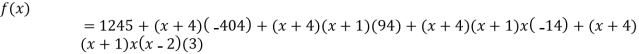
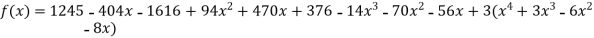
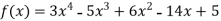
This is the required polynomial.
Q19) Deduce Lagrange’s formula for interpolation. The observed values of a function are respectively 168,120,72 and 63 at the four position3,7,9 and 10 of the independent variables. What is the best estimate you can for the value of the function at the position of the independent variable?
A19)
We construct the table for the given data:
X | 3 | 6 | 7 | 9 | 10 |
Y=f(x) | 168 | ? | 120 | 72 | 63 |
We need to calculate for x = 6, we need f (6) =?
Here 
We get 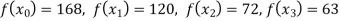
 By Lagrange’s interpolation formula, we have
By Lagrange’s interpolation formula, we have
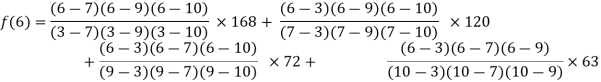
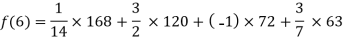
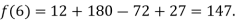
Hence the estimated value for x=6 is 147.
Q20) Find the polynomial of fifth degree from the following data
A20)
X | 0 | 1 | 3 | 5 | 6 | 9 |
Y=f(x) | -18 | 0 | 0 | -248 | 0 | 13104 |
A20)
Here 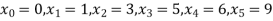
We get 
 By Lagrange’s interpolation formula
By Lagrange’s interpolation formula