Unit - 2
Numerical differentiation, integration and solution of differential equations
Q1) Given that
A1)
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find 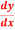 at
at 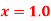 .
.
A1)
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y | 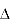 |  | 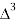 |
1.0 1.1 1.2 1.3 | 0.841 0.891 0.932 0.962 | 0.050 0.041 0.031 | -0.009 -0.010 | -0.001 |
By Newton’s forward differentiation formula for differentiation
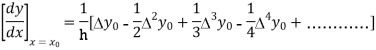
Here 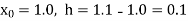
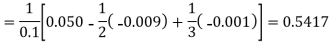
Q2) Given that
A2)
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find  ?
?
A2)
Backward difference table:
X | Y | 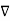 | 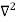 |  |
0.1 0.2 0.3 0.4 | 1.10517 1.22140 1.34986 1.49182 | 0.11623 0.12846 0.14196 | 0.01223 0.01350 | 0.00127 |
Newton’s Backward formula for differentiation
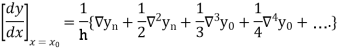
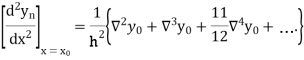
Here 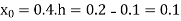


Q3) State Trapezoidal rule.
A3)
Let the interval [a, b] be divided into n equal intervals such that  <
< <…. <
<…. < =b.
=b.
Here 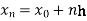 .
.
To find the value of 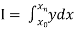 .
.
Setting n=1, we get
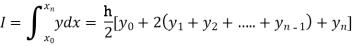
Or I = 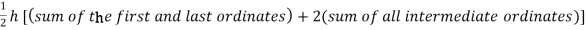
The above is known as Trapezoidal method.
Q4) State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below)
A4)
(0, 23), (0.5, 19), (1.0, 14), (1.5, 11), (2.0, 12.5), (2.5, 16), (3.0, 19), (3.5, 20), (4.0, 20).
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
A4)
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =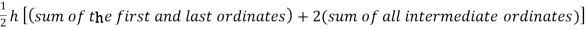
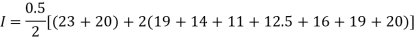


Q5) Compute the value of 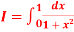
A5)
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
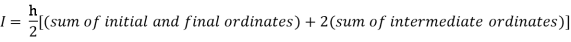
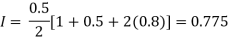
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
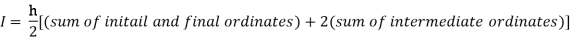
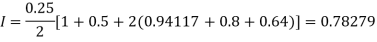
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
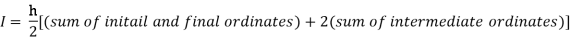
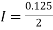 [(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
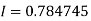
Q6) Write a short note on Simpson’s rule.
A6)
Generally fundamental theorem of calculus is used find the solution for definite integrals, but sometime integration becomes too hard to evaluate, numerical methods are used to find the approximated value of the integral.
Simpson’s rules are very useful in numerical integration to evaluate such integrals.
Here we will understand the concept of Simpson’s rule and evaluate integrals by using numerical technique of integration.
We find more accurate value of the integration by using Simpson’s rule than other methods
Simpson’s rule
We will study about Simpson’s one-third rule and Simpson’s three-eight rules.
But in order to get these two formulas, we should have to know about the general quadrature formula-
General quadrature formula-
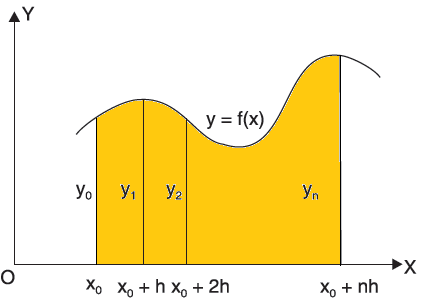
The general quadrature formula is gives as-

Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.
Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.
Simpson’s one-third rule-
Put n = 2 in general quadrature formula-
We get-

Note- the given interval of integration has to be divided into an even number of sub-intervals.
Simpson’s three-eighth rule-
Put n = 3 in general quadrature formula-
We get-

Note- the given interval of integration has to be divided into sub-intervals whose number n is a multiple of 3.
Q7) Evaluate the following integral by using Simpson’s 1/3rd and 3/8th rule.
A7)
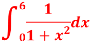
A7)
First, we will divide the interval into six parts, where width (h) = 1, the value of f(x) is given in the table below-
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
f(x) | 1 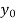 | 0.5 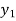 | 0.2 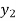 | 0.1 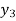 | 1/17 = 0.05884 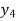 | 1/26 = 0.0385 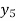 | 1/37 = 0.027 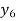 |
Now using Simpson’s 1/3rd rule-
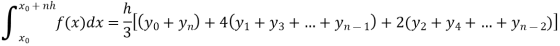
We get-

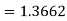
And now
Now using Simpson’s 3/8th rule-

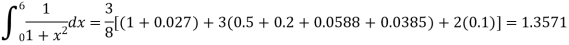
Q8) Estimate the value of the integral
A8)
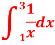
A8)
By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 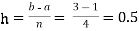
E construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
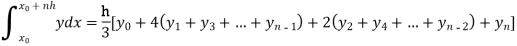
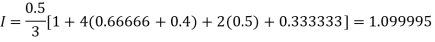
For n = 8, we have 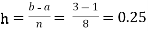
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule

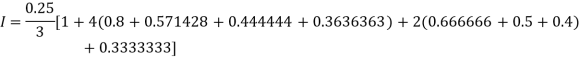

Q9) Using Simpson’s 1/3 rule with h = 1, evaluate
A9)

A9)
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
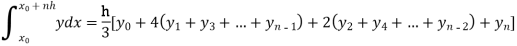

= 177.3853
Q10) Evaluate 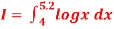
A10)
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
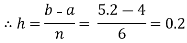
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4. 4 | 4.6 | 4.8 | 5.0 | 5.2 |
Y=logx | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule


= 1.8278475
Q11) Evaluate 
A11)
Here 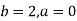
Using 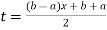 =
=
Also 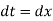
For 
For 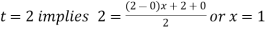
Hence 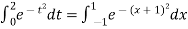
Here 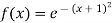
By Gauss quadrature 3-point rule
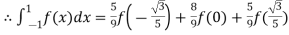

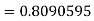
Q12) Solve by Gauss quadrature 3-point method 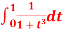
A12)
Given 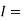
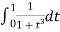
Here 
Using 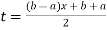 =
=
Also 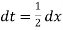
For 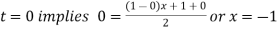
For 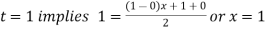
Hence 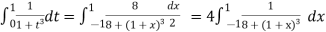
Here 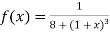
By Gauss quadrature 3-point rule
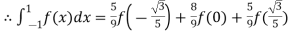
Hence 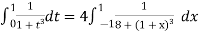
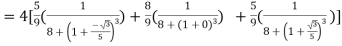

Q13) Define Euler’s method.
A13)
Euler’s method:
In this method the solution is in the form of a tabulated values
Integrating both side of the equation (i) we get
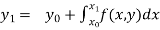
Assuming that 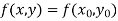 in
in 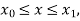 this gives Euler’s formula
this gives Euler’s formula
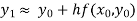
In general formula
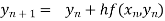 , n=0,1, 2…...
, n=0,1, 2…...
Error estimate for the Euler’s method
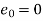

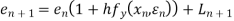
Q14) Use Euler’s method to find y (0.4) from the differential equation
A14)
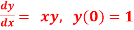 with h=0.1
with h=0.1
A14)
Given equation 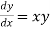
Here 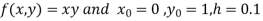
We break the interval in four steps.
So that 
By Euler’s formula
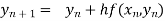 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
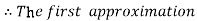
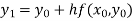
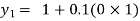
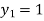
For n=1 in equation (i) we get
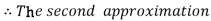
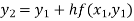

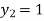 .01
.01
For n=2 in equation (i) we get
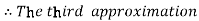
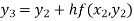
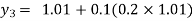

For n=3 in equation (i) we get
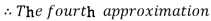
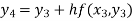

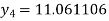
Hence y (0.4) =1.061106.
Q15) Given 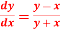 with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
A15)
Given equation is 
Here 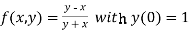
No. Of steps n=5 and so that 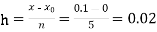
So that 
Also 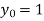
By Euler’s formula
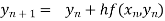 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
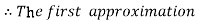

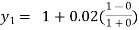
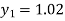
For n=1 in equation (i) we get
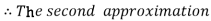

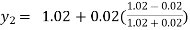
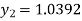
For n=2 in equation (i) we get

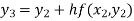
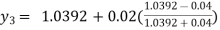

For n=3 in equation (i) we get
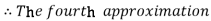

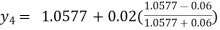
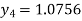
For n=4 in equation (i) we get


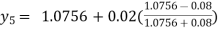
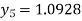
Hence 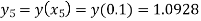
Q16) What is Euler’s modified method?
A16)
Modified Euler’s Method:
Instead of approximating 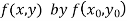 as in Euler’s method. In the modified Euler’s method, we have the iteration formula
as in Euler’s method. In the modified Euler’s method, we have the iteration formula

Where 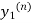 is the nth approximation to
is the nth approximation to  .The iteration started with the Euler’s formula
.The iteration started with the Euler’s formula
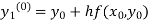
Q17) Using modified Euler’s method, obtain a solution of the equation
A17)
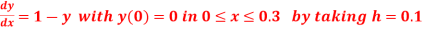
A17)
Given equation 
Here 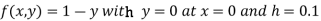
By modified Euler’s formula the initial iteration is
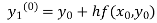


The iteration formula by modified Euler’s method is
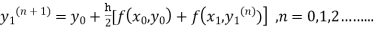 -----(i)
-----(i)
For n=0 in equation (i) we get

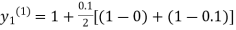
Where 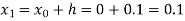 and
and 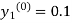 as above
as above
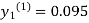
For n=1 in equation (i) we get


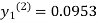
For n=2 in equation (i) we get
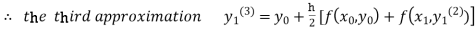

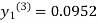
For n=3 in equation (i) we get
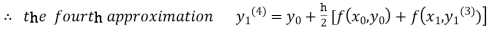
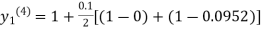
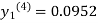
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
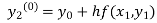
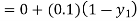

The iteration formula by modified Euler’s method is
 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
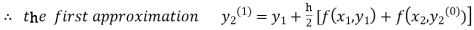
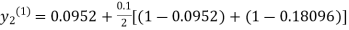
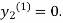 1814
1814
For n=1 in equation (ii) we get
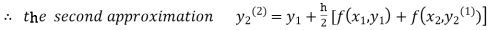
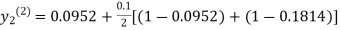
 1814
1814
Since first and second approximation are equal.
Hence y = 0.1814 at x=0.2
To calculate the value of 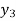 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is

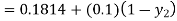

The iteration formula by modified Euler’s method is
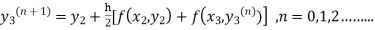 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
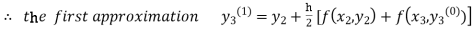
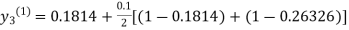
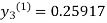
For n=1 in equation (iii) we get
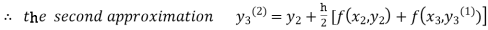
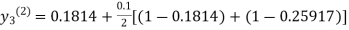
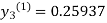
For n=2 in equation (iii) we get

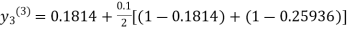

For n=3 in equation (iii) we get

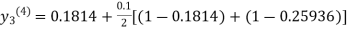
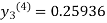
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Q18) Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
A18)
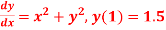
A18)
Given equation 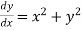
Here 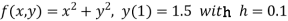
Also 
By Runge Kutta formula for first interval
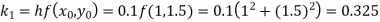

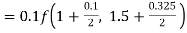
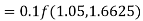

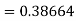

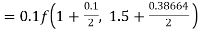

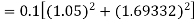
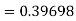
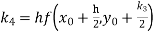

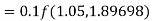
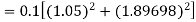
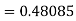
Again 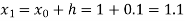
A fourth order Runge Kutta formula:
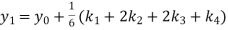


To find y at 
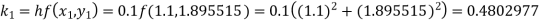
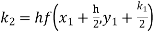
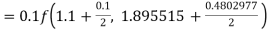

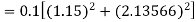
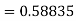
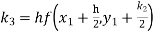


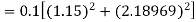
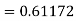
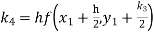
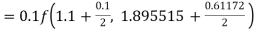
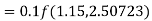
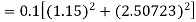

A fourth order Runge Kutta formula:

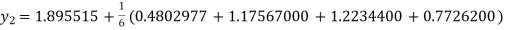

Q19) Using Runge Kutta method of fourth order, solve
A19)

A19)
Given equation 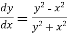
Here 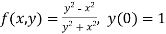
Also 
By Runge Kutta formula for first interval

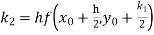
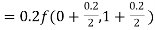
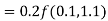
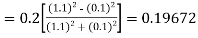

 )
)
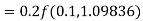
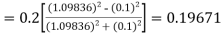
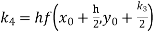

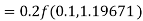

A fourth order Runge Kutta formula:
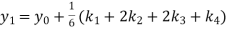
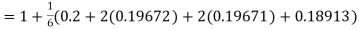
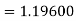
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 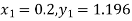

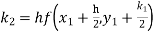
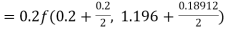

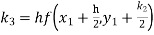
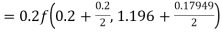
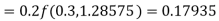
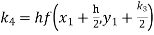


A fourth order Runge Kutta formula:

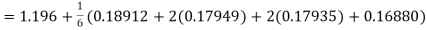

Hence at x = 0.4 then y=1.37527
Q20) Using Runge-Kutta method, solve
A20)
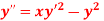 for
for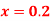 correct to four decimal places with initial condition
correct to four decimal places with initial condition 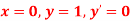
A20)
Given second order differential equation is
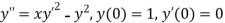
Let 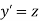 then above equation reduces to
then above equation reduces to
Or 
 (say)
(say)
Or  .
.
By Runge-Kutta Method we have

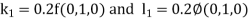

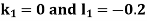



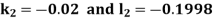
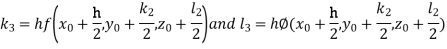
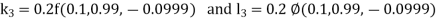
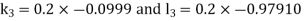
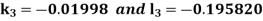
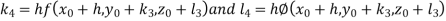



A fourth order Runge-Kutta formula:
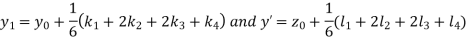

And 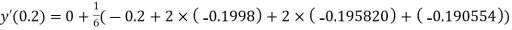
 .
.
Q21) Solve the boundary value problem defined by
A21)

By finite difference method. Compare the solution at y (0.5) by taking h=0.5 and h=0.25.
A21)
Given equation 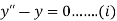
With boundary condition 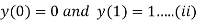
By finite difference method
 …. (iii)
…. (iii)
Putting(iii) in (i) we get
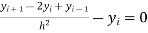 …. (iv)
…. (iv)
For h=0.5, here for 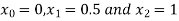 which corresponds to
which corresponds to 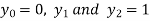
For i=1 in equation (iv) we get
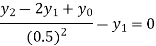

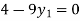

For h=0.25, here 
Which corresponds to 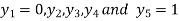
For i=1 in equation (iv) we get
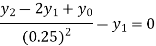
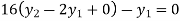
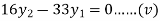
For i=2 in equation (iv) we get

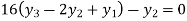
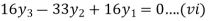
For i=3 in equation (iv) we get
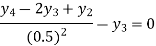
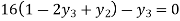

From equation (v), (vi) and (vii) we get
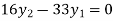
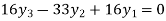

On solving above triangular equation we get

Hence for h=0.5 we get y (0.5) =0.44444
And for h=0.25 we get y (0.5) =0.443674