Unit - 5
Correlation and regression analysis
Q1) Define correlation.
A1)
If the change in one variable affects a change in other variable, then these two variables are said to be correlated.
Positive correlation- When both variables move in the same direction, or if the increase in one variable results in a corresponding increase in the other one is called positive correlation.

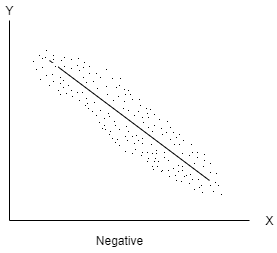
Negative correlation- When one variable increases and other decreases or vice-versa, then the variables said to be negatively correlated.
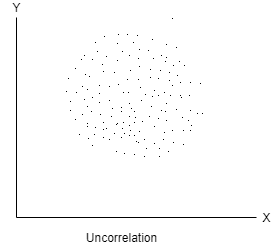
No correlation- When two variables are independent and do not affect each other then there will be no correlation between the two and said to be un-correlated.
Note- (Perfect correlation)- When a variable changes constantly with the other variable, then these two variables are said to be perfectly correlated.
Q2) What is Karl Pearson’s coefficient of correlation?
A2)
Karl Person’s coefficient of correlation is also called product moment correlation coefficient.
It is denoted by ‘r’, and defined as-

Here 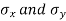 are the standard deviations of these series.
are the standard deviations of these series.
Alternate formula-
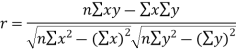
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Q3) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A3)
x | y | 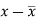 | 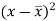 | 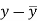 | 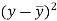 | ( 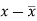 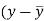 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
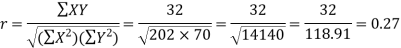
Q4) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
A4)
X | Y |  |  | 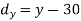 | 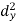 |  |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
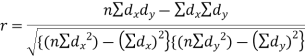
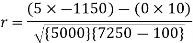

Q5) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A5)
The two lines of regression can be expressed as-
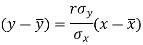
And
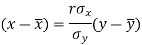
x | y | 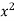 | 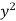 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
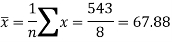
And
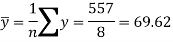
Standard deviation of x-
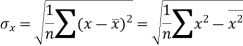

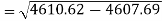
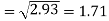
Similarly-
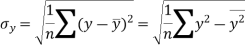
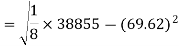
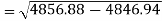
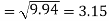
Correlation coefficient-
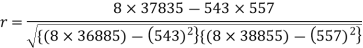
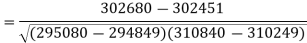
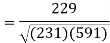
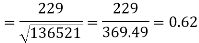
Put these values in regression line equation, we get
Regression line y on x-
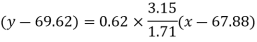
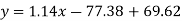
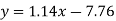
Regression line x on y-
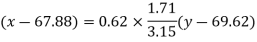
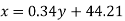
Q6) Derive Spearman rank correlation.
A6)
Spearman’s rank correlation-
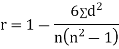
Let 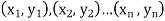 be the ranks of
be the ranks of 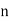 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 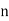 and hence their arithmetic means are, each
and hence their arithmetic means are, each
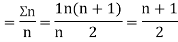
Let  ,
, 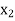 ,
, 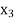 ,
,  be the values of variable
be the values of variable 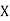 and
and 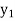 ,
,  ,
, 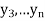 those of
those of 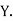
Then 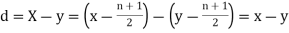
Where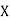 and y are deviations from the mean.
and y are deviations from the mean.
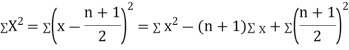

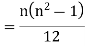
Clearly, 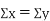 and
and 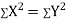

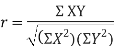
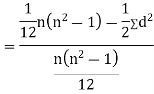
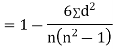
Q7) Compute the Spearman’s rank correlation coefficient of the dataset given below-
Person | A | B | C | D | E | F | G | H | I | J |
Rank in test-1 | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in test-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A7)
Person | Rank in test-1 | Rank in test-2 | d = 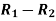 | 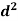 |
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
Sum |
|
|
| 280 |
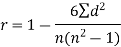

Q8) What is likelihood function?
A8)
Let  be a random sample of size n from a population with density function f (x.
be a random sample of size n from a population with density function f (x. 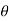 ). Then the likelihood function of the sample values
). Then the likelihood function of the sample values 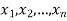 . Usually denoted by L = L (
. Usually denoted by L = L (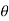 ) is their joint density function; given-by
) is their joint density function; given-by
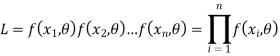
L gives the relative likelihood that the random variables assume a particular set of values 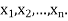 For a given sample
For a given sample  L becomes a function of the variable
L becomes a function of the variable 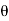 , the parameter.
, the parameter.
Q9) Prove that the. Maximum likelihood estimates of the parameter a of a population having density function:
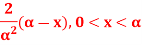
For a sample of, unit size is 2x. x being the sample value. Show also that the estimate is biased.
A9)
For a random sample of unit size (n = 1). The likelihood function is-

Likelihood equation gives-

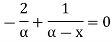

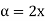
Hence MLE of 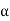 is given by
is given by 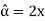
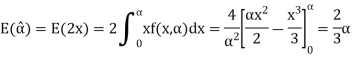
Since  is not an unbiased estimate of
is not an unbiased estimate of 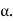
Q10) Write a short note on method of moments.
A10)
The principle of this method consists of equating the sample moments to the corresponding moments of the population, which are the function of unknown population parameter.
Here we will equate as many sample moments as there are unknown parameters and solve these simultaneous equations for estimating unknown parameter(s). This method of obtaining the estimate(s) of unknown parameter(s) is called “Method of Moments”.
Suppose 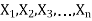 be a random sample of size n taken from a population whose probability density (mass) function is f(x,
be a random sample of size n taken from a population whose probability density (mass) function is f(x,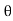 ) with k unknown parameters, say,
) with k unknown parameters, say, 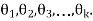
Then the r’th sample moment about origin is
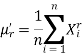
And about mean is
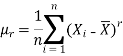
While the rth population moment about origin is
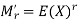
And about mean is
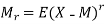
Generally, the first moment about origin (zero) and rest central moments (about mean) are equated to the corresponding sample moments. Thus, the equations are
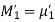
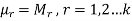
By solving these k equations for unknown parameters, we get the moment estimators.
Q11) Explain confidence intervals.
A11)
Let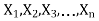 be a random sample of size n taken from normal population N (
be a random sample of size n taken from normal population N (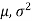 ) when
) when 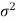 is known.
is known.
To find out the confidence interval for population mean, first of all we search the statistic for estimating μ whose distribution is known.
We know that when parent population is normal N (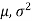 ) then sampling distribution of sample mean
) then sampling distribution of sample mean  is normally distributed with mean
is normally distributed with mean 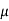 and variance
and variance  /n.
/n.
The variate

Follows the normal distribution with mean 0 and variance unity. Therefore, the probability density function of Z is
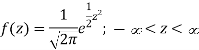
Here we will introduce two constants, 
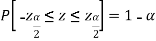
Where, 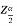 is the value of the variate Z having an area of
is the value of the variate Z having an area of  under the right tail of the probability curve of Z
under the right tail of the probability curve of Z
By putting the value of Z in above equation, we get-
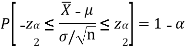
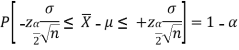
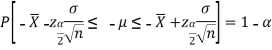
Multiplying each term by (-1) in above inequality, we get
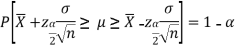
This can be rewritten as

Hence, (1-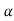 ) 100% confidence interval of population mean is given by
) 100% confidence interval of population mean is given by

Q12) The mean life of the bulbs manufactured by a company follows normal distribution with standard deviation 3200 hrs. A sample of 250 bulbs is taken and it is found that the average life of the bulbs is 50000 hrs with a standard deviation of 3500 hrs. Establish the 99% confidence interval within which the mean life of bulbs of the company is expected to lie.
A12)
Here, we have
n = 250 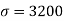 ,
,  and S = 3500
and S = 3500
Since population standard deviation i.e., population variance 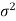 is known,
is known,
Therefore, we use (1-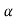 ) 100% confidence limits for population mean when population variance is known which are given by
) 100% confidence limits for population mean when population variance is known which are given by
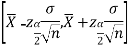
Where 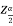 is the value of the variate Z having an area of
is the value of the variate Z having an area of  under the right tail of the probability curve of Z and for 99% confidence interval, we have
under the right tail of the probability curve of Z and for 99% confidence interval, we have
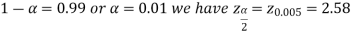
Therefore, the 99% confidence limits are

By putting the values of n, 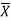 and σ, the 99% confidence limits are
and σ, the 99% confidence limits are
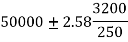
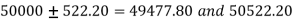
Hence, 99% confidence interval within which the mean life of bulb of the company is expected to lie is [49477.80, 50522.20].
Q13) What is p-value?
A13)
The p-value is the smallest value of level of significance (α) at which a null hypothesis can be rejected using the obtained value of the test statistic and it is defined as below-
The p-value is the probability of obtaining a test statistic equal to or more extreme (in the direction of sporting H1) than the actual value obtained when null hypothesis is true.
While testing a hypothesis, pre-selection of a significance level α does not account for values of test statistics that are “close” to the critical region.
Thus a test statistic value that is non-significant say for α = 0.05 may become significant for α = 0.01.
p-value approach is designed to give the user an alternative (in terms of probability) to a mere “reject” or “do not reject” conclusion.
Q14) A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
A14)
For v = 5, we have 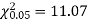
P, probability of getting a head=1/2; q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 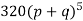
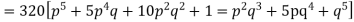
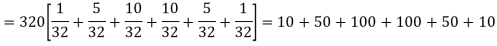
Thus, the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 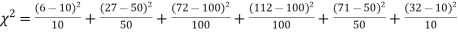

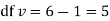
Since the calculated value of 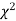 is much greater than
is much greater than 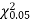 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Q15) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
A15)
The corresponding frequencies are
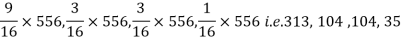
Hence,
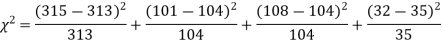
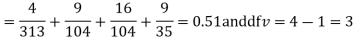
For v = 3, we have 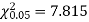
Since the calculated value of 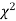 is much less than
is much less than  there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Q16) Explain the testing of hypothesis.
A16)
Hypothesis-
A hypothesis is a statement or a claim or an assumption about the value of a population parameter.
Similarly, in case of two or more populations a hypothesis is comparative statement or a claim or an assumption about the values of population parameters.
For example-
If a customer of a car wants to test whether the claim of car of a certain brand gives the average of 30km/hr is true or false.
Simple and composite hypotheses-
If a hypothesis specifies only one value or exact value of the population parameter then it is known as simple hypothesis. And if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.
Null and alternative hypothesis
The hypothesis which is to be tested as called the null hypothesis.
The hypothesis which complements to the null hypothesis is called alternative hypothesis.
In the example of car, the claim is 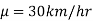 and its complement is
and its complement is 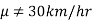 .
.
The null and alternative hypothesis can be formulated as-
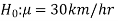
And
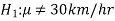
Q17) What are type-1 and type-2 errors?
A17)
Type-1 error-
The decision relating to rejection of null hypo. When it is true is called type-1 error.
The probability of type-1 error is called size of the test, it is denoted by 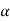 and defined as-
and defined as-
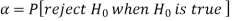
Note-
 is the probability of correct decision.
is the probability of correct decision.
Type-2 error-
The decision relating to non-rejection of null hypo. When it is false is called type-1 error.
It is denoted by 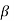 and defined as-
and defined as-
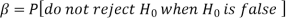
Decision |
 | 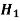 |
Reject 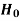 | Type-1 error | Correct decision |
Do not reject 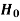 | Correct decision | Type-2 error |
Q18) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
A18)
It is given that-
Specified value of population mean = 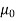 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
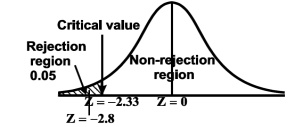
The null and alternative hypothesis will be-
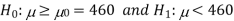
Also, the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by
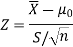
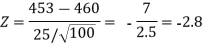
We get the critical value of left tailed Z test at 1% level of significance is 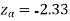
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Q19) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
A19)
We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
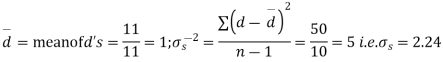
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.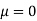
Then, 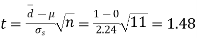 nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 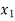 | 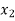 | 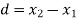 |  |  |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 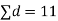 |
| 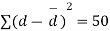 |
We find that 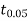 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of  , the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefitted by extra coaching.
Q20) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face-to-face mode yields examination results mean and SD respectively as-

And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?
A20)
Here we have-

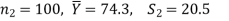
Here we wish to test that both educational methods are statistically equal. If 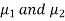 denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is 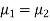 and its complement is
and its complement is 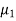 ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
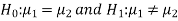
Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by
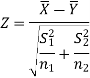

The critical (tabulated) values for two-tailed test at 5% level of significance are-
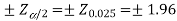
Since calculated value of Z (= 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
Reject the null hypothesis i.e., we reject the claim at 5% level of significance.