Unit - 1

Discrete Time System

Q1) For the system with y(t)=x(-t), find whether the system is linear or not?

Sol: To comment on linearity of system it should follow law of superposition. So, from model given below

Y(t)=ax1(-t)+bx2(-t)

Now from second model

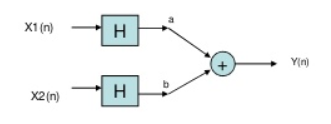
Y(t)= ax1(-t)+bx2(-t)

Since, output from both the model is same so system is linear.

Q2) For y(t)=cos[x(t)], comment whether it is time invariant or not?

 Sol: From model 1

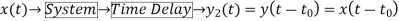
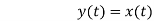
Y(t)=cos[x(t-t0)]

From model 2

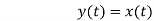
Y(t)=cos[x(t-t0)]

Since, time delay or advance in the input signal produces the corresponding change in the output. Hence, it is time invariant.

Q3) For y(t)=x(t2), is the system causal or anti causal?

Sol: y(t)= x(t2)

If the output for any time depends on the future than its not causal. So, Let t=1

Y(1)=x(1)

t=2

y(2)=x(4)

Since, it depends on future values, so it is anti-causal.

Q4) For y(t)=x(t)+2. Comment whether system has memory or memoryless?

Sol: For t=1

Y(1)=x(1)+2

For t=2

Y(2)=x(2)+2

So, for any value of t the output depends only on present input. Hence, it is memoryless.

Q5) For sequence h[n]={ 1, 2 , 1, -1} determine the response of system with input signal x[n] = {1, 2 ,3 ,1}

Sol:

a)     Finding x[k] and h[k] i.e n=k.

b)    Folding h[k] we get h[-k].

c)     Then shifting the above signal[-k] we get h[1-k]

d)    Multiplying above signal h[1-k] with x[n].

e)     Again, incrementing h[1-k] by 1 we get h[2-k] multiplying with x[n].

f)       Continuing this process till we get 0 for output y. In this case for n=5.

The graphical representation is shown below.

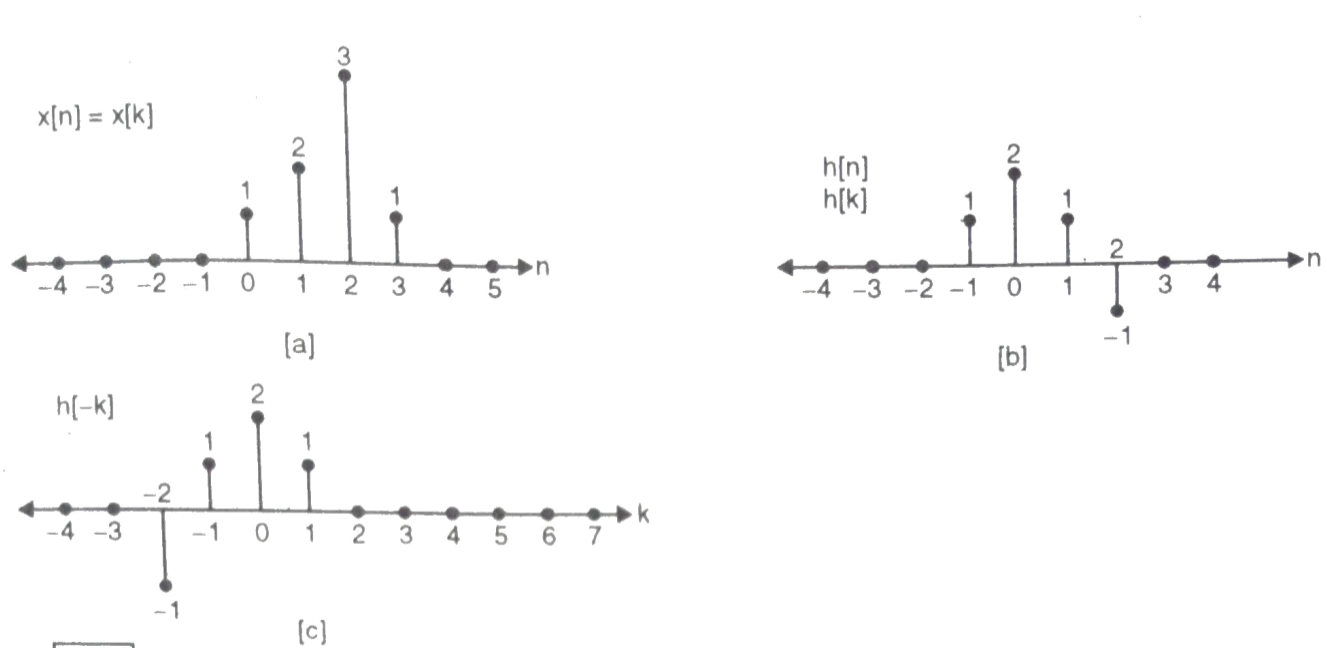
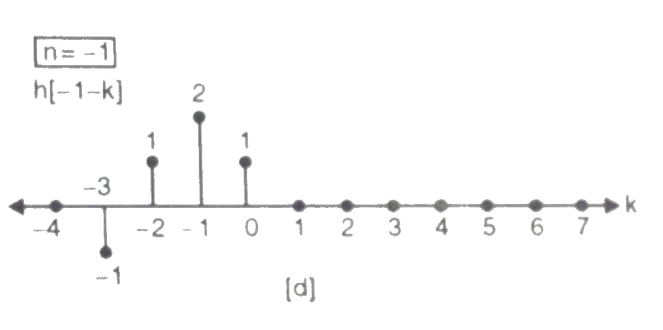
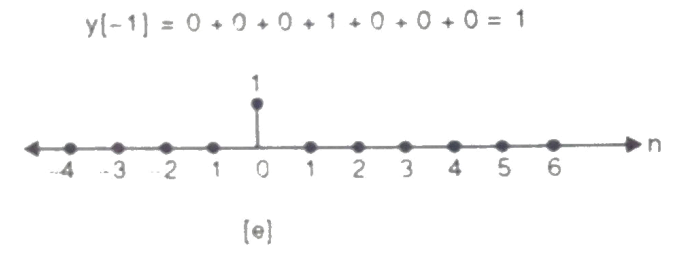
Q6) For h[n] = {1, 2, 1, -1}, x[n] = {1, 2, 3, 1}. Find x[n]*h[n]?

Sol:

y[-1] = 1

y[0]= 2+2 = 4

y[1] = 1+4+3 = 8

y[2]= -1+2+6+1 = 8

y[3]= -2+3+2 = 3

y[4]= -3+1 = -2

y[5]= -1

y[n]= {1, 4, 8, 8, -2, -1}

The above sequence is the required convolution of x[n] and h[n].

Q7) Determine the cross-correlation sequence rxy(l) of sequence

x[n] = {…… 0, 0, 0, -3, -2 ,1, 4, 8, -3, 0 ,0 ,0 ….}

y[n] = {…… 0, 0, 0, 1, 1, -1, 2, -2, 0 ,0 ,0 ….}

Sol: The cross-correlation is given as

rxy(l) = 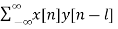                                l= 0, ±1, ±2,….

For l=0

rxy(l) =                               

M[n] = {…… 0, 0, 0, -3, -2 ,-1, -4, 16, 6, 0 ,0 ,0 ….}

For l=1

rxy(l) =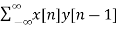            

x[n] = {-3, -2 ,1, 4, 8, -3}  

y[n]= {0, 1, 1, -1, 2, -2, 0}

y[n-1] = {0, 1, 1, -1, 2, -2}

rxy(l) = rxy(+1) = = -11

For l= 2

x[n] = {-3, -2 ,1, 4, 8, -3}  

y[n-2] = { 0,0, 1, 1, -1, 2, -2, 0}

rxy(l) = rxy(+2) = 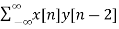= 16

 For l= 3

x[n] = {-3, -2 ,1, 4, 8, -3,0,0,0…}  

y[n-3] = {0, 0,0, 1, 1, -1, 2, -2, 0}

rxy(l) = rxy(+3) = 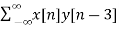= 9

For l = 4

x[n] = {-3, -2 ,1, 4, 8, -3,0,0,0…}  

y[n-4] = {0,0, 0,0, 1, 1, -1, 2, -2, 0}

rxy(l) = rxy(+4) = = 5

For l=5

x[n] = {-3, -2 ,1, 4, 8, -3,0,0,0…}  

y[n-5] = {0,0,0, 0,0, 1, 1, -1, 2, -2, 0}

rxy(l) = rxy(+5) = = -3

For l>6

rxy(l) = 0

Similarly finding for l= -1, -2,……

rxy(-l) = -14

rxy(-2) = -7

rxy(-3) = -3

rxy(-4) = -2

rxy(-5) = 6

rxy(-6) = 0

rxy(l) = {6, -2, -3, -7, -14, 14, -11, 16, 9, 5, -3}

Q8) Auto-correlate x[n] = {1,2,1,1}

Sol: rxx(l) =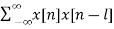

For l=0

rxx(0) =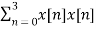

       =1x1+2x2+1x1+1x1=7

For l=1

rxx(1) =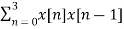

x[n-1] = {0,1,2,1,1} 

rxx(1) = 5

For l=2

rxx(2) = x[n-2] = {0,0,1,2,1,1} 

rxx(2) = 5

For l=3

rxx(3) = x[n-3] = {0,0,0,1,2,1,1} 

rxx(3) = 1

rxx(-1) =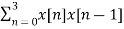

For l=-1

x[n+1] = {1,2,1,1,0} 

rxx(-1) = 5

For l= -2

rxx(-2) = x[n+2] = {1,2,1,1,0,0} 

rxx(-2) = 2

For l= -3

rxx(-3) = x[n+3] = {1,2,1,1,0,0,0} 

rxx(-3) = 1

rxx(l) = {1,3,5,7,5,3,1}

Q9) What are discrete time signals?

A9) If a discrete variable x(t) is defined at discrete time then x(t) is a discrete time signal. A discrete time signal is often identified as a sequence of number denoted by x(n), where ‘n’ is an integer.

Fig:1 Discrete time signal

Q10) Explain the types of discrete time systems?

A10) Even and Odd Signals

The even signals are symmetrical about Y-axis. They lie in first and second quadrants.

x[-n]=x[n]

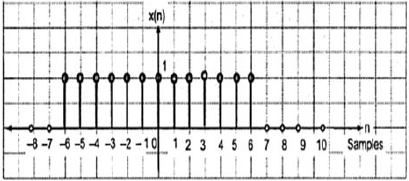
Fig:2 Even signal

The odd signals are symmetrical about origin. They lie in first and third quadrants.

x[-n]= -x[n]

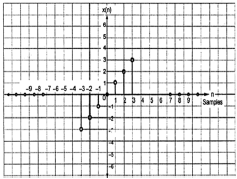
Fig:3 Odd signal

A signal having even and odd parts is mixed signal.

Periodic and Non-periodic signals:

A signal which repeats itself after a particular period of time is called as Periodic signal. The condition for any signal to be periodic is

x(n+N) = x(n)

considering a cosine signal −

x(n)=A cos(2πf0n+θ) x(n)= A cos(2πf0n+θ)

x (n +N) = A cos (2πf0(n +N) +θ)

                 =A cos(2πf0n+2πf0N+θ) x (n+ N)

                =A cos (2πf0(n +N) +θ) =A cos(2πf0n+2πf0N+θ)

                =A cos(2πf0n+2πf0N+θ) = A cos(2πf0n+2πf0N+θ)

For the signal to become periodic, following condition should be satisfied;

X (n+ N) = x(n) x (n +N) = x(n)

A cos(2πf0n+2πf0N+θ) =A cos(2πf0n+θ)

A cos(2πf0n+2πf0N+θ) = A cos (2πf0n+ θ)

As, 2πf0N is an integral multiple of 2π

2πf0N=2πK

N=Kf0

Frequencies of discrete sinusoidal signals are separated by integral multiple of 2π.

Energy and Power Signals

Energy Signal

Energy of a discrete time signal is denoted as E. It can be written as

E =

If each individual values of x(n)x(n) are squared and added, we get the energy signal. Here x(n) is the energy signal and its energy is finite over time i.e 0<E<∞

Power Signal

Average power of a discrete signal is represented as P. This can be written as

P =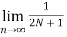

Q11) Explain linear and non-linear discrete time systems?

A11)

1)     Linear and Non-Linear system:

A system is said to be linear when it obeys law of superposition.

If we have two inputs x1(n) and x2(n), and output y(n). The operator ‘H’ is called linear operator if it satisfies the following condition.

Fig 4 Input first pass through adder

In the above figure first the two inputs pass through an adder than through the operator. So, the equation after adder will be ax1(n)+bx2(n). Now final output equation after passing through operator is

Y(n)=H[ax1(n)+bx2(n)]=Hax1(n)+H bx2(n)

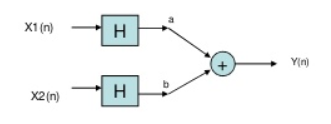
Fig 5 Input first pass through operator

Now, in above figure the two inputs first pass through the operator and then through the summer. The equation at output is

Y(n)= Hax1(n)+H bx2(n)

The two output equations in both the systems are same. Hence, the system operator H is linear.

Non-Linear system: If the system does not obey law of superposition, it is said to be non-linear.

2)     Time variant and Time Invariant system:  A time delay or advance in the input signal produces the corresponding change in the output. Then the system is said to be time invariant.

Fig:6 Time-Invariant system

 If the delay or advance in the system does not produce corresponding              change in the output then it’s called as Time variant System.

Q12) What is BIBO stability explain?

A12) BIBO stability stands for bounded input, bounded output stability. BIBO stability is the system property that any bounded input yields a bounded output. This is to say that as long as we input a signal with absolute value less than some constant, we are guaranteed to have an output with absolute value less than some other constant.

In order to understand this concept, we must first look more closely into exactly what we mean by bounded. A bounded signal is any signal such that there exists a value such that the absolute value of the signal is never greater than some value. Since this value is arbitrary, what we mean is that at no point can the signal tend to infinity, including the end behaviour.

Fig 7 Discrete time BIBO Stable System

Now that we have identified what it means for a signal to be bounded, we must turn our attention to the condition a system must possess in order to guarantee that if any bounded signal is passed through the system, a bounded signal will arise on the output. It turns out that a continuous-time LTI system with impulse response h[n] is BIBO stable if and only if it is absolutely summable. That is

Discrete-Time Condition for BIBO Stability

In the z-domain is about as easy to demonstrate as it is for continuous-time signals in the Laplace domain. However, instead of the region of convergence needing to contain the jω-axis, the ROC must contain the unit circle. Consequently, for stable causal systems, all poles must be within the unit circle.

Q13) Explain recursive and non-recursive discrete time systems?

A13) A recursive system is a system in which current output depends on previous output(s) and input(s) but in non-recursive system current output does not depend on previous output(s).

The system with memory is not necessarily a recursive system. For example: in FIR systems for input x[n] and output y[n] if we have

y[n] = 0.5(x[n]+x[n-1]) then the current output does not depend on previous output but depends on current input and previous input. But for IIR case like an accumulator

y[n] = y[n-1] + x[n], current output is depended on previous output as well as on current input (generally current and previous inputs). So, accumulator is a recursive system.

Q14) Derive equation for impulse response of discrete time systems?

A14) The LTI system can be represented by its impulse response with x(t) as its input signal and y(t) as its output.

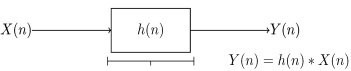
Fig 8 LTI System

Let input signal be x[n]

x[n] =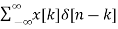

The output obtained when we apply input as unit sample sequence for n=k

y[n,k] = h[n,k] = H[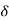[n-k]]

y[n] = H[x[n]]

         = H [ ]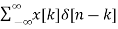

But y[n,k] = h[n,k] = H[[n-k]]

Hence, the output will now be

y[n] = [ ]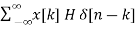

         = ]                                    

Q15) Compare discrete time and continuous time signals?

A15)