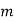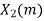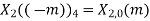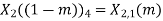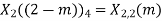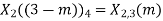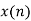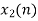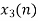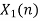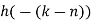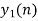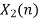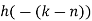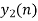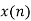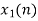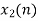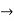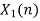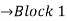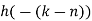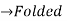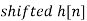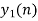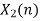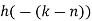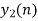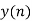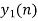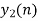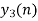Unit - 3
Discrete Fourier Transform
Q1) The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].
A1)
We know,
X[n] =x(nT)
= cos(200πnT)
= cos(2πn/3) , where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
Q2) Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of: X(t) = 1+ sin(2000πt) + cos (4000πt)
A2)
The frequencies are 0, 2000π and 4000π.
The Nyquist frequency is 4000π rad/s and the Nyquist rate is 8000π rad/s.
Q3) Consider an analog signal.  calculate Nyquist frequency?
calculate Nyquist frequency?
A3)
The frequency in the analog signal
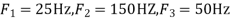
The largest frequency is
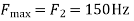
The Nyquist rate is
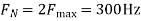
Q4) The analog signal 


A4)
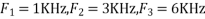
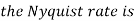

2. For 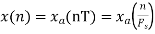


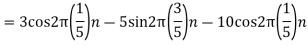
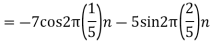
For 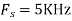 ,the folding frequency is
,the folding frequency is 
Hence 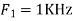 is not effected by aliasing
is not effected by aliasing
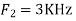 Is changed by the aliasing effect
Is changed by the aliasing effect 
 Is changed by the aliasing effect
Is changed by the aliasing effect 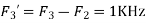
So that normalizing frequencies are
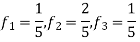
The analog signal that we can recover is
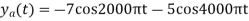
Which is different than the original signal 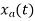
Q5) For 

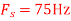
A5) a. 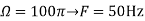
The minimum sampling rate is
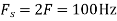
And the discrete time signal is
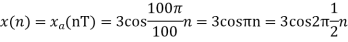
b. if 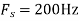 , the discrete time signal is
, the discrete time signal is

c. If Fs=75Hz , the discrete time signal is

d. For the sampling rate 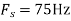
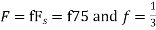 in part in (c). Hence
in part in (c). Hence
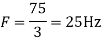
So, the analog sinusoidal signal is
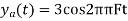
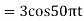
Q6) Suppose a continuous-time signal x(t) = cos (Ø0t) is sampled at a sampling frequency of 1000Hz to produce x[n]: x[n] = cos(πn/4). Determine 2 possible positive values of Ø0, say, Ø1 and Ø2. Discuss if cos(Ø1t) or cos(Ø2t) will be obtained when passing through the DC converter.
A6)
Taking T= 1/1000s
cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000)
Ø1 is easily computed as 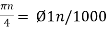
Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
 Ø2n/1000)
Ø2n/1000)
Ø2 = 2250π
Q7) Compute 4-point DFT of given sequence {1,0,0,1}. Use matrix for DFT computation?
A7)
x[n] = {1,0,0,1}
N-1 = 3
N= 4
W4 = 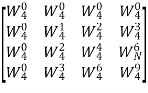 =
= 
X4 = 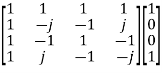
X4 = 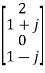
Q8) Compute the N-point DFT of x(n)=3δ(n).
A8)
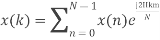
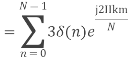
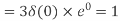
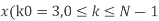
Q9) Compute the N-point DFT of x(n)=7(n−n0)
A9) We know that,

Substituting the value of x(n),
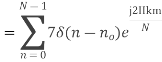
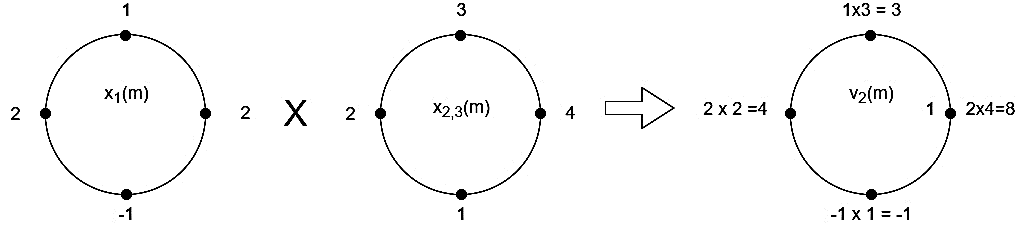
Q10) Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}
A10) 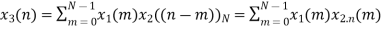
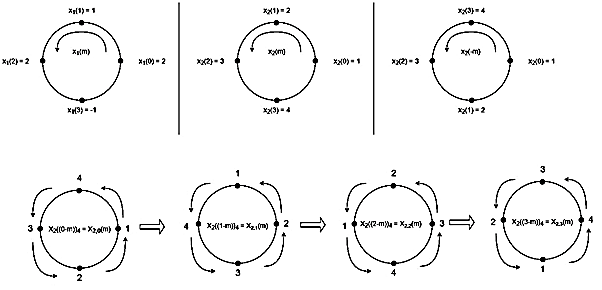
(2) 
When n=0; 

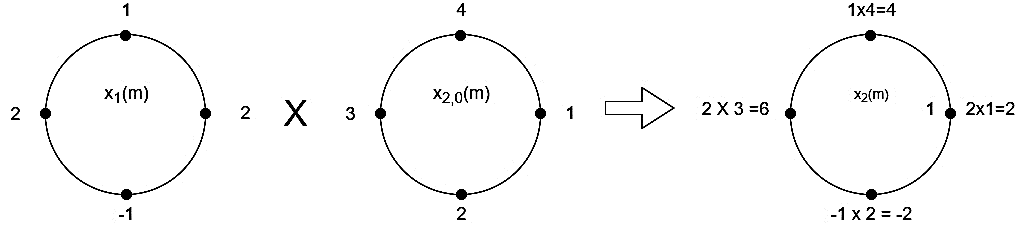
The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
When n=1; 

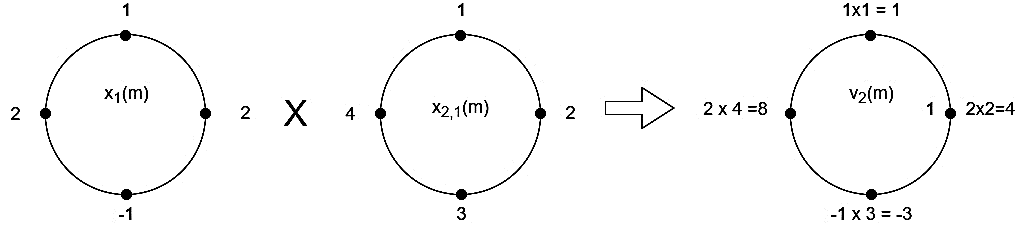
The sum of samples of v1(m) gives x2(1)
⸫ x3(1) =4 + 1 +8-3=10
(3)When n=2; 
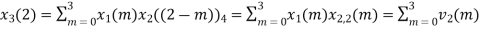
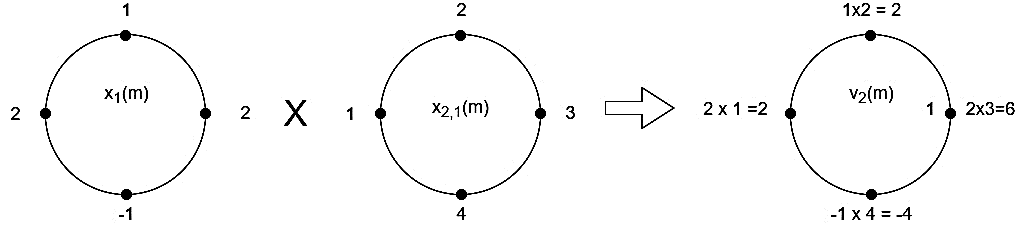
The sum of samples of v2(m) gives x3(2)
⸫ x3(2) = 6+2+2-4=6
(4) When n=3; 
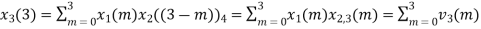
The sum of samples of v3(m) gives x3(3)
⸫ x3(3) =8+ 3+ 4-1= 14
x3(n) = {10,10,6,14}
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
|
|
| 2 | 1 | 2 | -1 |
|
|
|
| 1 | 2 | 3 | 4 |
| 4 | 3 | 2 | 1 | 4 | 3 | 2 |
|
| 4 | 3 | 2 | 1 | 4 | 3 |
|
|
| 4 | 3 | 2 | 1 | 4 |
|
|
|
| 4 | 3 | 2 | 1 |
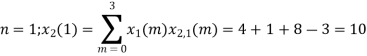

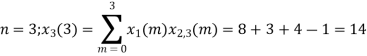
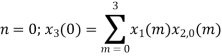
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
Q11) The unit sample response sequence of a system h[n] = {3,2,1}. Use the overlap save method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,-2,-1,0}. Take N=8.
A11)
8=L+2
L=6
The length of block selected is 6.
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
|
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | … |
|
| 0) | 2 | 0 | -2 | 0 | 2 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 | … |
 Block 1
Block 1  Zeros added
Zeros added
 Block 2
Block 2
 Block 3
Block 3
h[n] = {3,2,1,0,0,0,0,0}
| Periodic extension of data block 1 | Data block 1 | ||||||||||||||
| 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 4 | 1 | 6 | 4 | -4 | 4 | 4 | 7 | |
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
| 1 | 0 | -2 | -1 | 0 | 2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | 4 | 5 | 4 | |
Fig 8 Final answer from overlap save method
Q12) The unit sample sequence of a system is h[n] = {3,2,1}. Use overlap add method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,0,-2,-1,0}. Take N=8.
A12)
8=L+2
L=6
From input every time 6 elements are selected and two zeros (M-1) are padded after them as shown below.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … |
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | -2 | 0 | … |
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -2 | 0 | … |
|
Fig 10 Breaking up long input sequence into blocks of data
h[n] = {3,2,1,0,0,0,0,0}
| Periodic extension of data block 1 | Data block 1 |
| ||||||||||||||||
| 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |
| |||
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |
| |||
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
| -2 | -1 | 0 | 2 | 0 | 0 | 0 | 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 | |
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | X | X | … |
Fig 10 Final answer from overlap add method
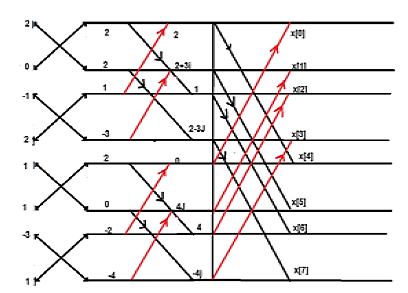
Q13) Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.
A13) Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Q14) Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
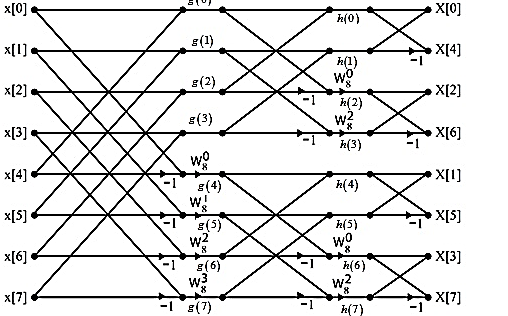
X(0)= 20 X(4) =0
X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141
X(2) = 0 X(6) = 0
X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142