Unit - 1
Cartesian
Q1) Obtain the unit vector in the direction from the origin towards the point P (3, -3, -2)
A1)
The origin O (0,0,0) while P (3, -3, -2) hence the distance vector 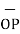 is
is
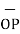 = (3-0)
= (3-0) 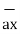 + (-3-0)
+ (-3-0) 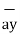 +(-2-0)
+(-2-0)  = 3
= 3 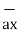 -3
-3 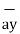 -2
-2 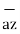
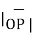 =
= 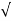 (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
 OP=
OP= 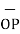 / |
/ |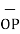 | = 3
| = 3 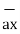 -3
-3  -2
-2  / 4.6904 =
/ 4.6904 =
= 0.6396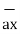 -0.63963
-0.63963 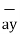 -0.4264
-0.4264 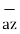
Q2) Given the three points in cartesian co-ordinate system as A (3, -2,1) B (-3, -3,5), C (2,6, -4)
Find
i) The vector from A to C
ii) The unit vector from B to A
A2) The position vectors for the given points are:
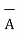 = 3
= 3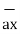 - 2
- 2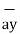 +
+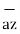 .
.
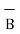 = -3
= -3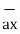 - 3
- 3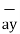 +5
+5 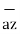 .
.
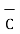 = 2
= 2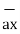 +6
+6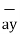 -4
-4 .
.
i) The vector from A to C is
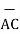 =
= 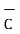 -
- 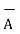 = [ 2-3]
= [ 2-3] 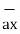 + [6– (-2)]
+ [6– (-2)]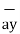 + [-4-1]
+ [-4-1] 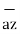 .
.
= - 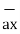 + 8
+ 8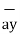 -5
-5 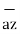 .
.
ii) For unit vector from B to A obtain the distance vector 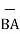 first
first
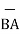 =
=  -
- 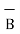
= [ 3 – (-3)]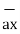 + [ (-2) – (-3)]
+ [ (-2) – (-3)] 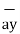 + [ -4-1]
+ [ -4-1] 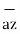
= 6 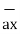 +
+  -4
-4 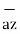 .
.
|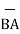 | =
| = 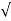 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
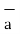 BA =
BA =  / |
/ | | = 6
| = 6 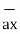 +
+ 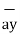 -4
-4 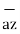 ./ 7.2801
./ 7.2801
Q3) Given the three points in cartesian co-ordinate system as A (3, -2, 1) B (-3, -3,5), C (2,6, -4)
Find
i) The distance from B to C
ii) The vector from A to the mid-point of the straight-line joining B to C.
A3) The position vectors for the given points are:
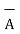 = 3
= 3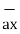 - 2
- 2 +
+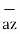 .
.
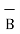 = -3
= -3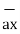 - 3
- 3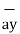 +5
+5  .
.
 = 2
= 2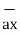 +6
+6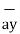 -4
-4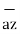 .
.
i) For distance between B and C
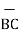 =
= 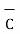 -
-  = [ 2 – (-3]
= [ 2 – (-3] 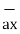 + [6-(-3)]
+ [6-(-3)]  + [-4) – (-5)]
+ [-4) – (-5)]  = 5
= 5 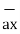 + 9
+ 9 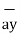 – 9
– 9 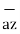
Distance BC =  2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
ii) Let B (x1, y1, z1) and C (x2, y2, z2) then the co-ordinates of the mid-point BC are (x1+x2/2, y1+y2/2, z1+z2/2)
Q4) A charge Q1=-20µC is located at P (-6,4,6) and a charge Q2=50µC is located at R (5,8, -2) in a free space. Find the force exerted on Q2 by Q1 in vector form. The distances given are in meters.
A4) From the co-ordinates of P and R the respective position vectors are:
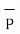 = -6
= -6 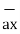 + 4
+ 4 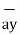 + 6
+ 6 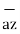
and
 = 5
= 5 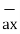 + 8
+ 8 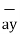 -2
-2 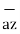
The force on Q2 is given by
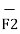 = Q1 Q2 / 4 π
= Q1 Q2 / 4 π  R212.
R212.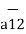
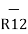 =
= 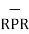 =
= 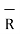 -
- 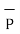 = [ 5 – (-6)]
= [ 5 – (-6)] 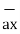 + (8-4)
+ (8-4) 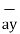 + [-2-(-6)
+ [-2-(-6) 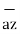 ]
]
= 11 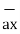 + 4
+ 4  - 8
- 8 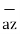
|R12| = 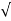 (11) 2 + (4) 2 +(-8) 2 = 14.1774
(11) 2 + (4) 2 +(-8) 2 = 14.1774
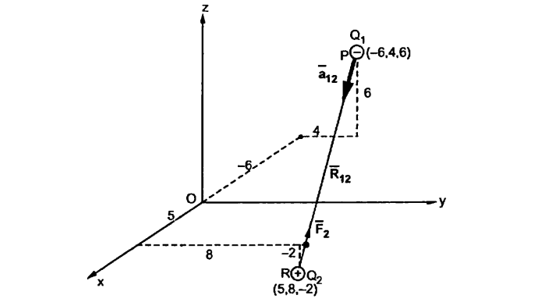
 =
= 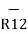 / |
/ | | = 11
| = 11 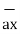 + 4
+ 4 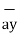 -8
-8 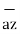 / 14.1774
/ 14.1774
 = -20 x 10 -6 x 50 x 10 -6 / 4 π x 8.854 x 10 -12 x (14.1774) 2 [
= -20 x 10 -6 x 50 x 10 -6 / 4 π x 8.854 x 10 -12 x (14.1774) 2 [ 
= -0.0447 [ 0.7758 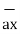 + 0.2821
+ 0.2821  - 0.5642
- 0.5642 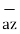 ]
]
= -0.0346 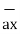 - 0.01261
- 0.01261 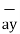 + 0.02522
+ 0.02522 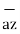 N
N
This is the required force exerted on Q2 by Q1
The magnitude of the force is
|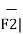 =
= 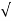 (0.0346) 2 + (0.01261) 2 + (-0.02522) 2 = 44.634mN
(0.0346) 2 + (0.01261) 2 + (-0.02522) 2 = 44.634mN
Q5) A scalar field is given by



Find its gradient at P (0,1,1) for Cartesian, P (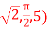 for cylindrical and P
for cylindrical and P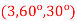 for the spherical.
for the spherical.
A5)
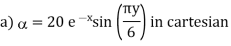
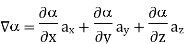
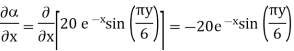

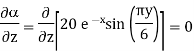
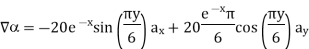
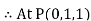 the
the 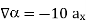 +9.0689
+9.0689 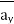
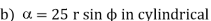
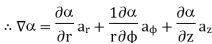
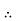 At
At 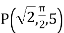 the
the 

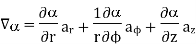
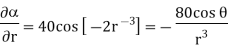
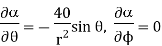
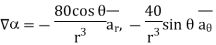

Q6) Find the expression of energy stored in magnetic field?
A6) Let us consider the magnetic field is due to electromagnet that is a coil of several no. turns.
This coil or inductor is carrying current I when it is connected across a battery or voltage source through a switch.
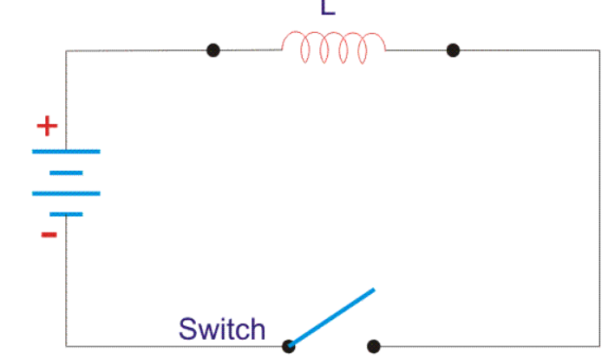
Figure. Inductor circuit
Suppose battery voltage is V volts, value of inductor is L Henry, and current I will flow at steady state.
When the switch is ON, a current will flow from zero to its steady value. But due to self- induction an induced voltage appears which is
E = -L dI/dt ---------------------------------------------------------------------(1)
Here E always in the opposite direction of the rate of change of current.
The energy or work done due to this current passing through this inductor is U. As, the current starts from its zero value and flows against the induced emf E, the energy will grow up gradually from zero value to U.
dU = W. dt, where W is the small power and W = – E.I
So, the energy stored in the inductor is given by
dU = W. dt = -E. I dt = L dI/dt. I dt = LIdI
Now integrate the energy from 0 to its final value.
U =  =
=  dI = ½ LI 2
dI = ½ LI 2
Again
L = 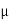 o N 2 A /l
o N 2 A /l
where N is the number of turns of the coil,
A is the effective cross-sectional area of the coil and l is the effective length of the coil.
Again,
I = H.l/N
Where, H is the magnetizing force, N is the number of turns of the coil and l is the effective length of the coil.
I = B.l/ 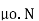
Now putting expression of L and I in equation of U, we get new expression i.e.
U = μoN2 A /l. B.L/ μo N / 2 = B 2 Al/ 2 μo
Q7) What are scalar and vector fields?
A7) If at every point of a region, there is corresponding value of some physical function, the region is called a field. Mathematically, a field is a function which describes a physical quantity at all points in space. Field is classified as scalar or vector.
i) Scalar field: If the value of the physical function at every point is scalar quantity, then the field is scalar field for example temperature of atmosphere density of the nonhomogeneous body and electric potential scalar field.
ii) Vector field: If the value of the physical function at every point is vector quantity, the field is vector field for example the wind velocity of atmosphere, gravitational force and electric field intensity are vector fields.
Q8) Write the expressions for line, surface and volume integral?
A8) Line Integrals
It is defined as any integral which is to be determined along a curve. Line integral can be defined in terms of limits of sum as are the integrals of ordinary calculus.
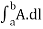

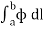
Above mentioned are some examples of line integrals calculated from point a to point b. In first case each element of length dl on the curve is multiplied by the local value A scalarly and then these products are summed to get the value of the integral.
Line integral in terms of cartesian coordinate can be represented as

Surface Integrals
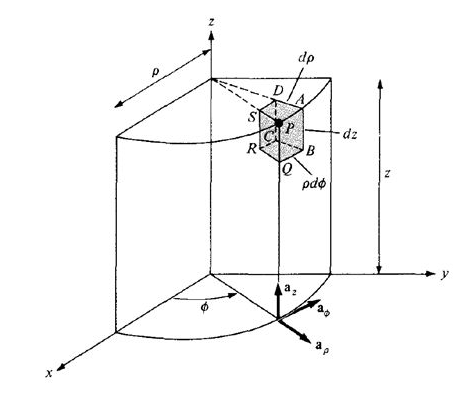
Fig: A two-sided surface
Differential Distances: 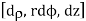
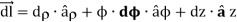
Differential Surfaces:


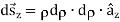
Different Volume:
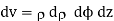
Volume Integrals
If a closed surface in space enclosing a volume V is considered then the integrals
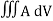
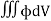
Are the examples of volume integrals. Since volume is a three-dimensional quantity and hence three integrals.
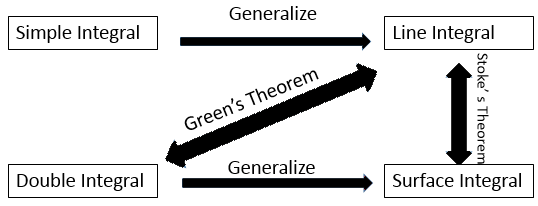
Q9) Draw a block diagram to show the relation between line surface and volume integral. How they are related by Green’s theorem?
A9)
Q10) Define Coulombs Law?
A10) It states that force between two-point charges Q1 and Q2
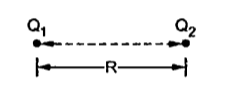
Figure. Two point charge
Consider two point charges Q1 and Q2 as shown in the figure seperated by distance R. The charge Q1 exerts a force on Q2 while Q2 also exerts a force on Q1. The force acts along the line joining Q1 and Q2. The force exerted between them is repulsive if the chrages are of same polarity while it is attractive if the charges are of different polarity.
Mathematically the force F between the charges can be expressed as,
F α Q1Q2/ R 2
Q1Q2------ Product of two charges
R ------- Distance between the two charges
The law also states that the force depends on the medium in which the point charges are located. The effect of medium is introduced in the equation of force as a constant of proportionality denoted as k.
F = k. Q1 Q2/ R2
The constant of proportionality takes into account the effect of medium.
Therefore,
k = 1/ 4 π 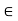
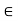 = Permittivity of medium in which charges are located. The units of
= Permittivity of medium in which charges are located. The units of 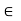 are farads/metre(F/m)
are farads/metre(F/m)
In general,  is expressed as,
is expressed as,
 =
= 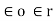
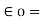 Permittivity of free space or vacuum
Permittivity of free space or vacuum
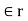 = Relative permittivity or dielectric constant of the medium with respect to free space.
= Relative permittivity or dielectric constant of the medium with respect to free space.
 Absolute permittivity
Absolute permittivity
For free space or vacuum the relative permittivity 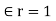 hence
hence
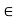 =
= 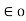
F = 1/ 4 π 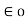 . Q1Q2/ R2
. Q1Q2/ R2
The value of permittivity of free space 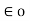 is
is
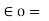 1/ 36 π x 10 -9 = 8.854 x 10 -12 F/m
1/ 36 π x 10 -9 = 8.854 x 10 -12 F/m
k = 1/ 4π 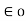 = 1/ 4π x 8.854 x 10 -12 = 8.98 x 10 9 = 9 x 10 9 m/F
= 1/ 4π x 8.854 x 10 -12 = 8.98 x 10 9 = 9 x 10 9 m/F
Hence the Coulombs law can be expressed as,
F = Q1 Q2 / 4π 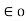 R 2
R 2
This the force between the two-point charges located in free space or vacuum.
Q11) Define electric field intensity and also derive its expression?
A11) Consider a point charge Q1 as shown in figure:

Fig: Electric Field Intensity
If any other similar charge Q2 is brought near it Q2 experiences a force. Infact if Q2 is moved around Q1 still Q2 experiences a force as shown in figure.
Thus, there exists a region around a charge in which it exerts force on any other charge. This region where a particular charge exerts a force on any other charge located in that region called electric field of that charge. The electric field of Q1 is shown in figure (b).
The force experienced by the charge Q2 due to Q1 is given by Coulombs law as,
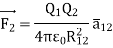
Thus, force per unit charge can be written as:
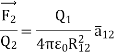
This force exerted per unit charge is called electric field intensity or electric field strength. It is a vector quantity and is directed along a segment from the charge Q1 to the position of any other charge.
It is denoted as 
Another definition of electric field is the force experienced by a unit positive test charge that is Q2 = 1C.
Consider a charge Q1 as shown in figure below. The unit positive charge Q2=1C is placed at distance R from Q1. Then the force acting on Q2 due to Q1 is along the unit vector  . As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity
. As the charge Q2 is unit charge the force exerted on Q2 is nothing but electric field intensity 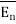 of Q1. Then the force acting on Q2 due to Q1 is along the unit vector
of Q1. Then the force acting on Q2 due to Q1 is along the unit vector 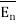 . As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity
. As the charge Q2 is unit charge the force exerted onQ2 is nothing but electric field intensity 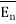 of Q1 at a point where unit charge is placed.
of Q1 at a point where unit charge is placed.
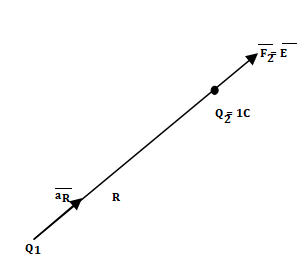
Fig: Concept of electric field intensity

If a charge Q1 is located at the centre of the spherical coordinate system then unit vector  in equation (3) becomes the radial unit vector
in equation (3) becomes the radial unit vector 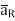 coming radially outwards from Q1 and the distance R is the radius of the sphere r.
coming radially outwards from Q1 and the distance R is the radius of the sphere r.
Q12) Define electric flux?
A12) The region in which the influence of an electric charge can be felt is known as electric field. The force experienced by a unit positive charge at a point is called is electric field strength.
E= F/q N/C or V/m
Electric flux density is defined as the amount of flux passes through unit surface area in the space at right angle to the direction of electric field.
E = 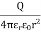
Q: charge
r: distance between the object and field
Q13) Define Gauss Law and also prove it?
A13) The surface integral of electrostatic field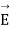 produced by any source over any closed surface S enclosing a volume V in vacuum i.e., total electric flux over the closed surface S in vacuum is X the total charge (
produced by any source over any closed surface S enclosing a volume V in vacuum i.e., total electric flux over the closed surface S in vacuum is X the total charge ( ) contained inside S i.e.
) contained inside S i.e.
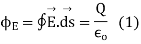
The charge inside S maybe point charges as well as continuous charge distributions.
The surface chosen to calculate the surface integral is called Gaussian surface.
Proof: -
Suppose an isolated positive point charge q is situated at the centre of the sphere of radius r,
According to coulomb’s law, electric field intensity at every point on the surface of the sphere is
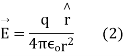
Where is unit vector directed from +q to the surface element
is unit vector directed from +q to the surface element
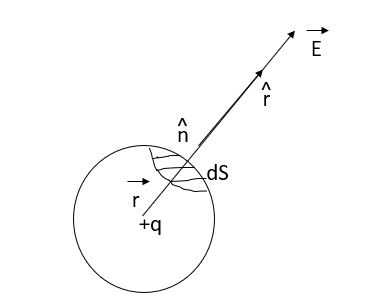
Fig: Charge q at centre of Sphere
Consider small area element ds represented by the vector where is unit vector  along out drawn normal to the area element
along out drawn normal to the area element

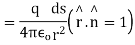
Integrating over the closed surface area of sphere we get
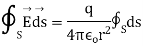

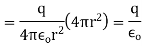
Which proves gauss theorem.
If there are two-point charges 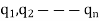 lying inside the surface, each will contribute the electric flux independent of the others.
lying inside the surface, each will contribute the electric flux independent of the others.
(Superposition principle)
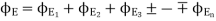
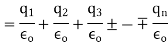
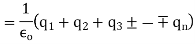
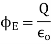
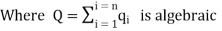 sum of all the charges inside the closed surface if the medium surrounding the charge has a dielectric constant K, then
sum of all the charges inside the closed surface if the medium surrounding the charge has a dielectric constant K, then
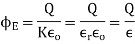
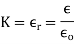
If there is no net charge within the closed surface that is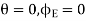
Q14) Derive Poisons equation?
 .
.  =
= 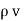
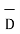 = flux density
= flux density
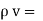 Volume charge density.
Volume charge density.
For a homogeneous isotropic and linear medium, flux density and the electric field are directly proportional. Thus,
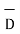 =
= 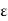 .
. 
 .
. 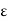 .
.  =
= 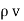
From the gradient relationship
E = - 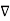 . V
. V
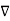 .
. 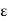 (-
(-  . V) =
. V) = 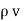
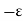 (
(  .
. 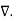 V) =
V) = 
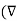 .
. 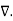 V) =-
V) =- 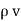 /
/ 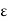
Now 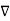 .
. 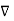 operation is called ‘del squared’ operation denoted as
operation is called ‘del squared’ operation denoted as  2.
2.
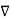 2. V = -
2. V = - 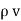 /
/ 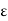
This equation is called as Poisson’s Equation
Q15) Derive Laplace equation and mention the application of Laplace and Poisons equation?
A15) If in a certain region volume charge density is zero ( 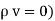 which is true for dielectric medium then the Poisson’s equation takes the form,
which is true for dielectric medium then the Poisson’s equation takes the form,
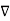 2. V =0.
2. V =0.
This equation is called Laplace’s equation.
Application of Laplace and Poisson’s Equations
Using Laplace or Poisson’s equation we obtain:
We can also obtain capacitance between these two surfaces.