Unit - 5

Formulation of Field Equations

Q1) Derive electric field and magnetic field wave equation?

A1) Maxwell’s equation can be combined into a wave equation by making use of the vector identity

                                           (1)

Let us apply the identity above to the Maxwell’s electric field curl equation

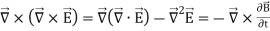            (2)

In a region of space free of charges, ∇~ ·E~ = 0. Assuming that we are only interested in well-behaved analytic functions (i.e., those for which we can reverse the order of differentiations with impunity), we can transform the magnetic field term in Equation 2 from the curl of a time derivative to the time derivative of a curl.

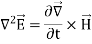
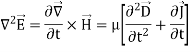
If we assume that the region of interest is also current-free, we can replace D~ with E~ to obtain

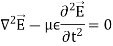
Above equation is the wave equation for electric field. Similarly, the wave equation for magnetic field is given below

Q2) Explain types of waveguides?

A2) Waveguide is a linear structure that conveys EM waves between its end points. At frequencies more the 3GHz losses in the transmission line and cable become significant due to losses that occur in the dielectric needed to support the conductor and within the conductor itself. In general, a waveguide consists of hollow metallic tube of a rectangular or circular shape used to guide an EM wave by successive reflections from the inner walls of tube.

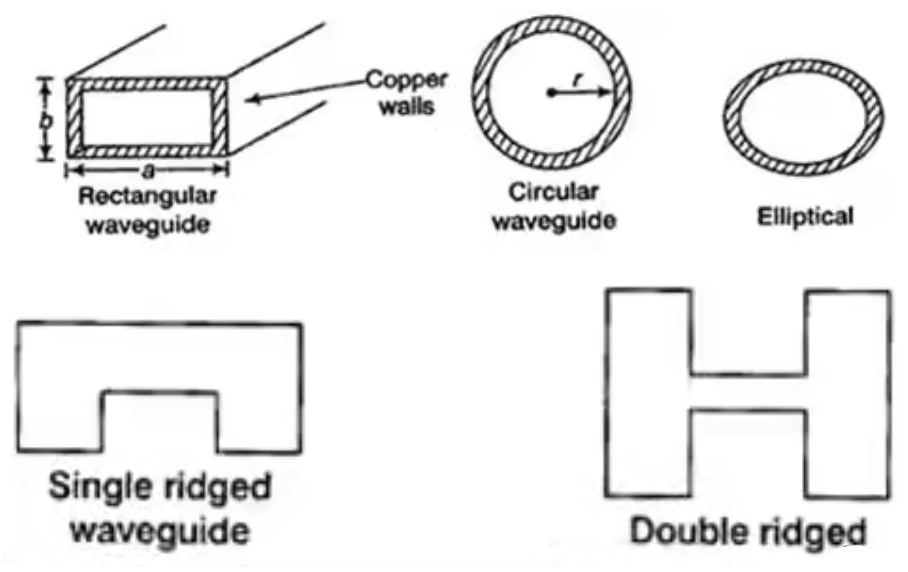
Fig: Types of waveguides

In the waveguide no traverse electromagnetic mode can exist but TE and TM wave can exist. The dominant mode in particular guide is the mode having the lowest cut-off frequency.

Q3) Define parallel plate waveguide and derive expression for electric field in it?

A3) For a parallel-plate waveguide, the plates are infinite in the y-extent; we need to study the propagation in the z-direction. The following assumptions are made in the wave equation.

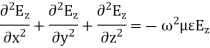
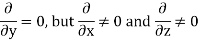
These two conditions define the TE modes and the wave equation.

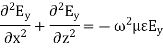
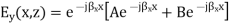
At x = 0, Ey = 0 which leads to A + B = 0. Therefore, A = -B = Eo/2j, where Eo is an arbitrary constant

At x = a, Ey (x, z) = 0. Let a be the distance separating the two PEC plates

Moreover, from the differential equation

where m = 1, 2, 3, ... Since propagation is to take place in the z direction, for the wave to propagate, we must have z 2 > 0, or

This leads to the following guidance condition which will ensure wave propagation The cutoff frequency fc is defined to be at the onset of propagation

The cutoff frequency is the frequency below which the mode associated with the index m will not propagate in the waveguide. Different modes will have different cutoff frequencies. The cutoff frequency of a mode is associated with the cutoff wavelength c

Each mode is referred to as the TEm mode. It is obvious that there is no TE0 mode and the first TE mode is the TE1 mode.

Q4) Define parallel plate waveguide and derive expression for magnetic field in it?

A4) Magnetic Field

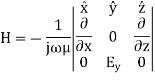
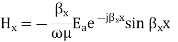
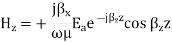
As can be seen, there is no Hy component, therefore, the TE solution has Ey, Hx and Hz only.

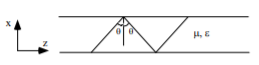
From the dispersion relation, it can be shown that the propagation vector components satisfy the relations

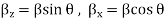
where  is the angle of incidence of the propagation vector with the normal to the conductor plates. The phase and group velocities are given by

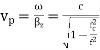  and

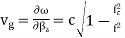
The effective guide impedance is given by:

Q5) Derive TM mode for parallel plate waveguide?

A5)

The magnetic field also satisfies the wave equation

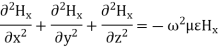
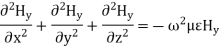
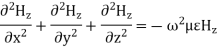
For TM modes, we assume

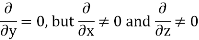
Assume only

These two conditions define the TM modes

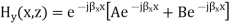
From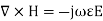

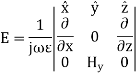
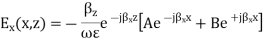
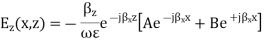
At x=0, Ez = 0 which leads to A = B = Ho/2 where Ho is an arbitrary constant. This leads to

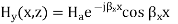
At x =a, Ez = 0 which leads to

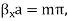where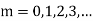

This defines the TM modes which have only Hy, Ex and Ez components. The effective guide impedance is given b

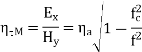
Q6) For parallel plate waveguide list the equation for TE and TM modes?

A6) For TE Mode

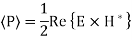
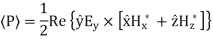
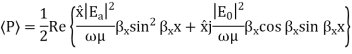
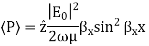
For TM Mode

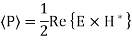
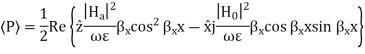
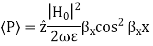
Q7) What are basic equations involved in rectangular waveguide for E and H?

A7) Rectangular waveguide is situated in the rectangular coordinate system with its breadth along x-direction, width along y-direction and z-indicates direction of propagation. Vector Helmholtz equation is

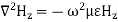
For TE wave (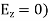

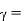Propagation constant

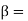Phase constant

 = attenuation constant

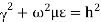
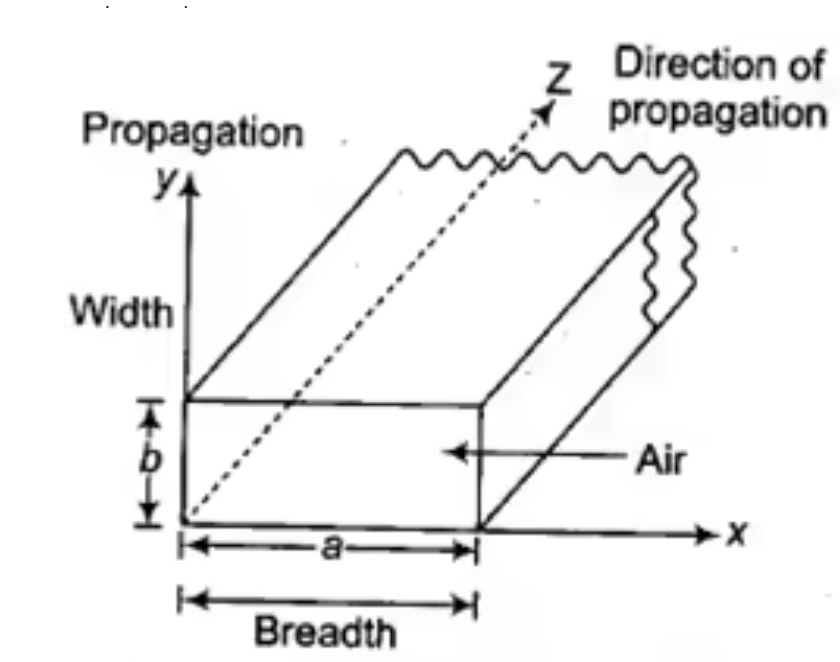
Fig: Rectangular Waveguide

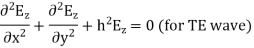
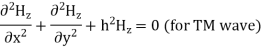
Solving above equations we fi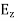nd and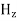

Also applying Maxwell equations, we can find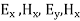

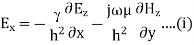
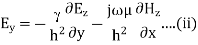
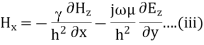
Q8) Derive expression for TE mode of propagation in a rectangular waveguide?

A8) TEmn modes in rectangular cavity are characterized by Ez = 0 which means z component of magnetic field Hz must be existing in order to have energy transmission in guide. TEmn field equation in rectangular wave guide are

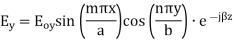
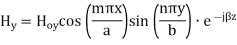
Propagation Constant:

The propagation of the wave in the guide is assumed in positive z- direction. Propagation constant 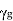in waveguide differs from intrinsic propagation constant  of dielectric.

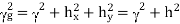
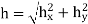is cut-off wave number

For lossless dielectric

Cut-off Wave Number

The Cut-off Wave Number h is defined by

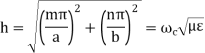
for 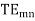mode

There are three cases for the propagation constant 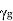in waveguide.

Case 1:

If 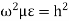, then 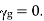Hence there will be no wave propagation (evanescence) in the guide.

Thus at a given operating frequency f, only those mode having f>fc will propagate, and

Modes with 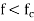will lead to imaginary β (or real ).

Such modes are called evanescent modes. The cut-off frequency is

Case 2:

If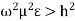

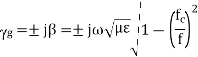
Case 3:

If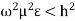

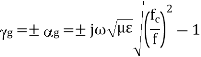
So, wave cannot propagate through waveguide as 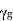is a real quantity

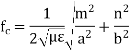
For free space/loss less dielectric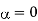

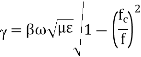
The phase velocity in the positive z-direction for the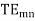

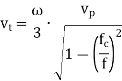
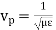is the phase velocity in vacuum.

The characteristic wave impedance of 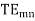mode in the guide

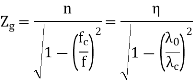
Q9) Derive expression for TM mode of propagation in rectangular waveguide?

A9) The EM wave inside rectangular waveguide has an infinite number of patterns called as modes. Generally, two types of mode (TE and TM) are present in the waveguide. These modes are denoted as TEmn and TMmn.

m=half wave variation along wider dimension a

n= Half wave variation along narrow dimension b

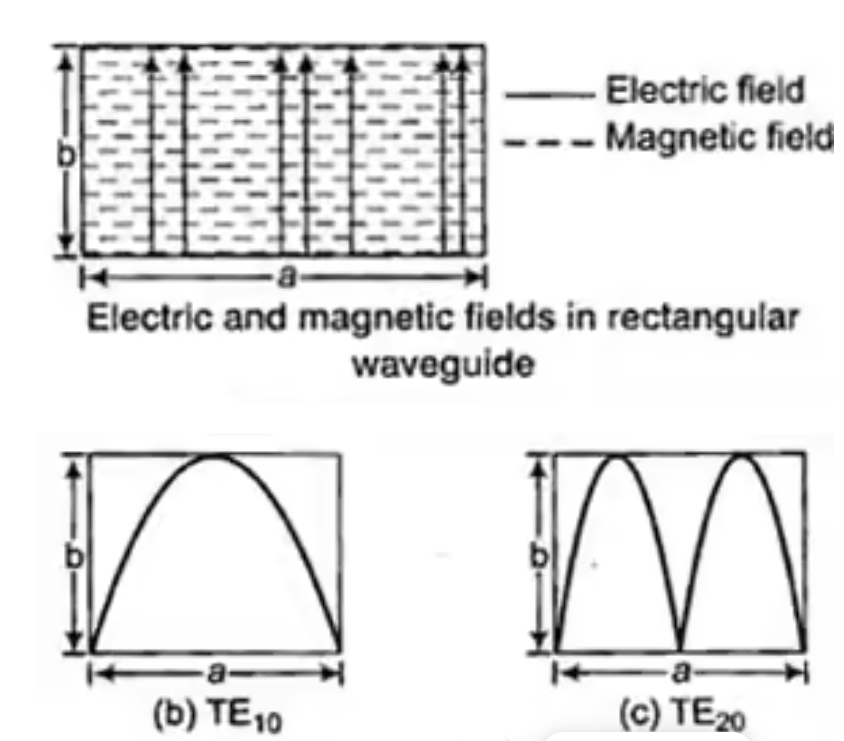
Fig: TE10 and TE20 mode in rectangular waveguide

TM modes of propagation in a Rectangular waveguide

For TM mode the z component of electric field E must exist in order to have energy transmission in the guide.

The mode field equations are

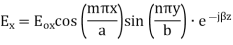
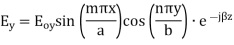
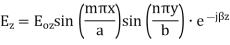
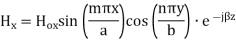
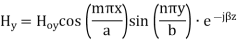
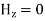
Some of the TM mode characteristic equations are same as that of TE mode but some are different and they are given as

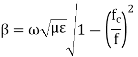
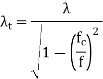
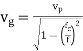
Q10) Define half wave dipole antenna?

A10) The dipole antenna is cut and bent for effective radiation. The length of the total wire, which is being used as a dipole, equals half of the wavelength (i.e., l = λ/2). Such an antenna is called as half-wave dipole antenna. This is the most widely used antenna because of its advantages. It is also known as Hertz antenna. The range of frequency in which half-wave dipole operates is around 3KHz to 300GHz. This is mostly used in radio receivers.

It is a normal dipole antenna, where the frequency of its operation is half of its wavelength. Hence, it is called as half-wave dipole antenna.

The edge of the dipole has maximum voltage. This voltage is alternating (AC) in nature. At the positive peak of the voltage, the electrons tend to move in one direction and at the negative peak, the electrons move in the other direction. This can be explained by the figures given below.

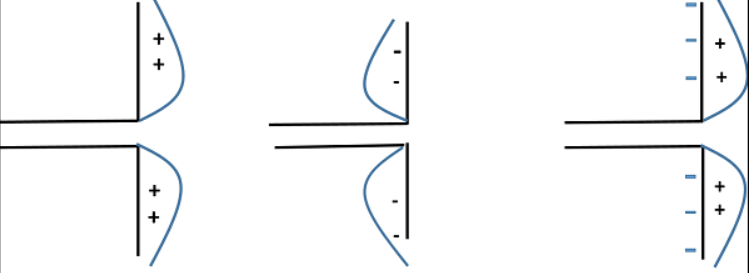
Fig: Half wave Dipole

The cumulative effect of this produces a varying field effect which gets radiated in the same pattern produced on it. Hence, the output would be an effective radiation following the cycles of the output voltage pattern. Thus, a half-wave dipole radiates effectively.

Q11) Explain the radiation pattern of half wave dipole antenna?

A11) The radiation pattern of this half-wave dipole is Omni-directional in the H-plane. It is desirable for many applications such as mobile communications, radio receivers etc.

Fig: Radiation Pattern of Half-wave Dipole

The above figure indicates the radiation pattern of a half wave dipole in both H-plane and V-plane.

The radius of the dipole does not affect its input impedance in this half wave dipole, because the length of this dipole is half wave and it is the first resonant length. An antenna works effectively at its resonant frequency, which occurs at its resonant length.

Q12) Explain Yagi uda antenna?

A12) It is the most commonly used type of antenna for TV reception over the last few decades. It is the most popular and easy-to-use type of antenna with better performance, which is famous for its high gain and directivity. The frequency range in which the Yagi-Uda antennas operate is around 30 MHz to 3GHz which belong to the VHF and UHF bands.

A Yagi-Uda antenna was seen on top of almost every house during the past decades. The parasitic elements and the dipole together form this Yagi-Uda antenna. The figure shows a Yagi-Uda antenna. It is seen that there are many directors placed to increase the directivity of the antenna. The feeder is the folded dipole. The reflector is the lengthy element, which is at the end of the structure.

Fig: Yagi Uda Antenna

The center rod like structure on which the elements are mounted is called as boom. The element to which a thick black head is connected is the driven element to which the transmission line is connected internally, through that black stud. The single element present at the back of the driven element is the reflector, which reflects all the energy towards the direction of the radiation pattern. The other elements, before the driven element, are the directors, which direct the beam towards the desired angle.

The directional pattern of the Yagi-Uda antenna is highly directive as shown in the figure given below.

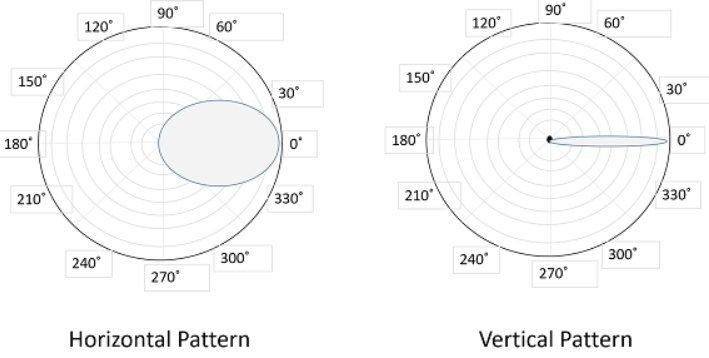
Fig: Yagi Uda Antenna

The minor lobes are suppressed and the directivity of the major lobe is increased by the addition of directors to the antenna.

Q13) Explain parabolic reflector antenna?

A13) Parabolic Reflectors are Microwave antennas. The frequency range used for the application of Parabolic reflector antennas is above 1MHz. These antennas are widely used for radio and wireless applications. The standard definition of a parabola is - Locus of a point, which moves in such a way that its distance from the fixed point (called focus) plus its distance from a straight line (called directrix) is constant.

The following figure shows the geometry of parabolic reflector. The point F is the focus (feed is given) and V is the vertex. The line joining F and V is the axis of symmetry. PQ are the reflected rays where L represents the line directrix on which the reflected points lie (to say that they are being collinear). Hence, as per the above definition, the distance between F and L lie constant with respect to the waves being focussed.

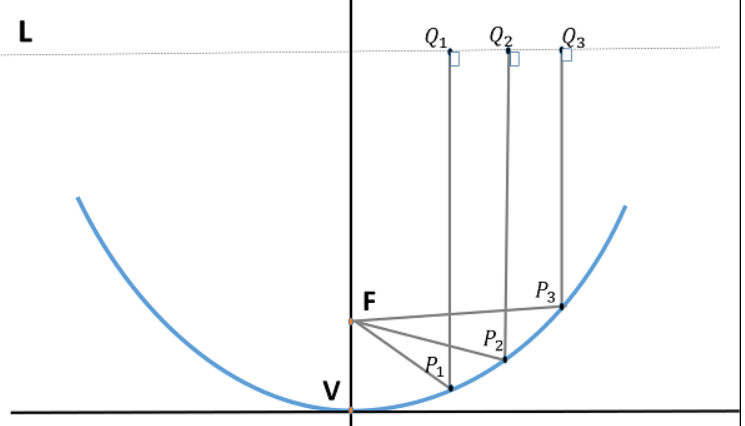
Fig: Parabolic Antenna

The reflected wave forms a collimated wave front, out of the parabolic shape. The ratio of focal length to aperture size (i.e., f/D) known as “f over D ratio” is an important parameter of parabolic reflector. Its value varies from 0.25 to 0.50.

The law of reflection states that the angle of incidence and the angle of reflection are equal. This law when used along with a parabola, helps the beam focus. The shape of the

Parabola when used for the purpose of reflection of waves, exhibits some properties of the parabola, which are helpful for building an antenna, using the waves reflected.

If a Parabolic Reflector antenna is used for transmitting a signal, the signal from the feed, comes out of a dipole or a horn antenna, to focus the wave on to the parabola. It means that, the waves come out of the focal point and strike the Paraboloidal reflector.

The gain of the paraboloid is a function of aperture ratio (D/λ). The Effective Radiated Power (ERP) of an antenna is the multiplication of the input power fed to the antenna and its power gain. Usually, a wave guide horn antenna is used as a feed radiator for the paraboloid reflector antenna.

Q15) Explain Cassegrain feed?

A15) Cassegrain is another type of feed given to the reflector antenna. In this type, the feed is located at the vertex of the paraboloid, unlike in the parabolic reflector. A convex shaped reflector, which acts as a hyperboloid is placed opposite to the feed of the antenna

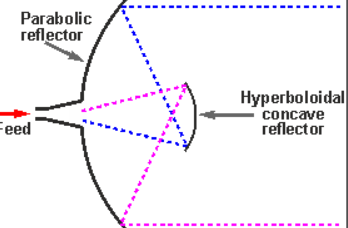
Fig: Cassegrain Feed

It is also known as secondary hyperboloid reflector or sub-reflector. It is placed such that it’s one of the foci coincides with the focus of the paraboloid. Thus, the wave gets reflected twice.