Unit - 1
Introduction
Q1) Find the four-point DFT of the sequence
A1)
x(n) = {0,1,2,3}
A1) Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 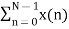 e-j2 π nk/N
e-j2 π nk/N
X (0) =
X (0) = x (0) + x (1) +x (2) + x (3) = 0 +1+2+3 = 6
X (1) = 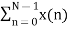 e-j2 π nk/N
e-j2 π nk/N
X (1) = 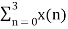 e-j2 π n/4
e-j2 π n/4
= x (0) e0 + x (1) e –j2 π /4+ + x (2) e-j4 π/4+ x (3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X (2) = 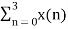 e-j2 π n2/4
e-j2 π n2/4
X (2) =  e-j π n
e-j π n
X (2) = x (0) 1+ x (1) e-j π + x (2) e-j2 π + x (3) e-j3 π
X (2) = -2
X (3) =  e-j2 π n3/4
e-j2 π n3/4
X (3) = x (0) e0 + x (1) e-j3 π/2 + x (2) e-j3 π + x (3) e-j9 π/2
X (3) = -2-2j.
DFT = {6, -2+2j, -2, _2-2j}
Q2) Shown in figure below is a system in which the sampling signal is an impulse train with alternating sign
A2)
(a)
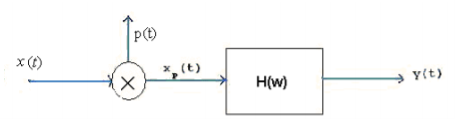
The sampling signal p(t), the Fourier Transform of the input signal x(t) and the frequency response of the filter are shown below:
(b)

-WM Wm
(c)

(d)
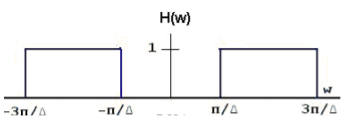
Find:
For  < π / 2wM sketch the Fourier transform of xp(t) and y(t).
< π / 2wM sketch the Fourier transform of xp(t) and y(t).
For,  < π / 2wM determine a system that will recover x(t) from xp (t) and another that will recover x(t) from y(t).
< π / 2wM determine a system that will recover x(t) from xp (t) and another that will recover x(t) from y(t).
What is the maximum value  in relation to wM for which x(t) can be recovered from either xp(t) or y(t)?
in relation to wM for which x(t) can be recovered from either xp(t) or y(t)?
A2) As xp(t) = x(t) p(t)
By dual of convolution theorem, we have Xp(w) = X(w) P(w)
So, we first find the Fourier Transform of p(t) as follows:
The Fourier Transform of a periodic function is an impulse train at intervals of. Strength of impulse at being:
Ck= π / 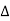
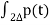 ej 2π Kt /
ej 2π Kt /  dt ------------(1)
dt ------------(1)
= π / 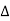 (1- ej 2π Kt /
(1- ej 2π Kt / 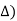
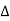 = π /
= π / 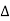 ( 1 – e jk π) -------------------(2)
( 1 – e jk π) -------------------(2)
= π / 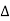 ( 1 – (-1) k) ------------(3)
( 1 – (-1) k) ------------(3)
Thus P(w) =
Thus, we sketch Xp(w) and Y(w) as
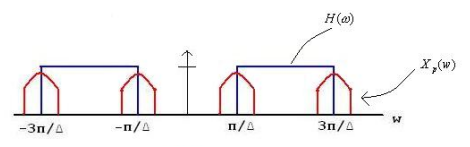
Which is equal to

To recover x(t) from xp(t):
Modulate xp(t) with cos (π/ . t)
. t)
Cos (π/ . t) has a spectrum with impluses of equal strength at -π/
. t) has a spectrum with impluses of equal strength at -π/ and π/
and π/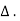
Thus, the new signal will have copies of the original spectrum (modulated by a constant of-course) at all even multiples of π/ .
.
Now an appropriate Low-pass filter can extract the original spectrum!
To recover x(t) from y(t):
Here too, notice from the figures that modulation of cos (π/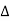 . t) with will do the job. Here too, the modulated signal will have copies of the original spectrum at all even multiples of
. t) with will do the job. Here too, the modulated signal will have copies of the original spectrum at all even multiples of
π/
So long as adjacent copies of the original spectrum do not overlap in Xp(w) theoretically one can reconstruct the original signal. Therefore, the condition is:
2wM < 2π/ ---
--- 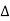 < π/ w M
< π/ w M
Q3) The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].
A3)
We know,
X[n] =x(nT)
= cos(200πnT)
= cos(2πn/3), where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
Q4) Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of:
A4)
X(t) = 1+ sin(2000πt) + cos (4000πt)
A4) The frequencies are 0, 2000π and 4000π.
The Nyquist frequency is 4000π rad/s and the Nyquist rate is 8000π rad/s.
Q5) Consider an analog signal 
A5)
Find the Nyquist rate?
A5) The frequency in the analog signal
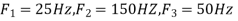
The largest frequency is
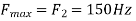
The Nyquist rate is

Q6) The analog signal 
A6)
- What is the Nyquist rate for this signal?
- Using a sampling rate
 . What is discrete time signal obtained after sampling?
. What is discrete time signal obtained after sampling? - What is analog signal
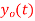 we can reconstruct from the samples if we use ideal interpolation?
we can reconstruct from the samples if we use ideal interpolation?
A6)
- The frequency of the analog signal is

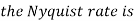

- For


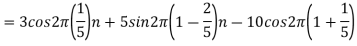


For  ,the folding frequency is
,the folding frequency is 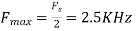
Hence 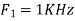 is not affected by aliasing
is not affected by aliasing
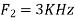 Is changed by the aliasing effect
Is changed by the aliasing effect 
 Is changed by the aliasing effect
Is changed by the aliasing effect 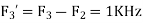
So that normalizing frequencies are
The analog signal that we can recover is
Which is different than the original signal 
Q7) For 
A7)
- Find the minimum sampling rate required to avoid aliasing.
- If
 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling? - If
 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling? - What is the frequency F of a sinusoidal that yields sampling identical to obtained in part c?
A7) a. 
The minimum sampling rate is
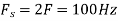
And the discrete time signal is

b. If 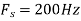 , the discrete time signal is
, the discrete time signal is
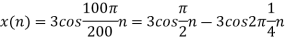
c. If Fs=75Hz, the discrete time signal is
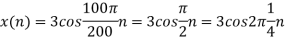
d. For the sampling rate 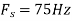
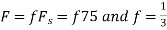 in part in (c). Hence
in part in (c). Hence
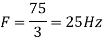
So, the analog sinusoidal signal is
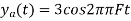
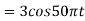
Q8) Suppose a continuous-time signal x(t) = cos (Ø0t) is sampled at a sampling frequency of 1000Hz to produce x[n]: x[n] = cos(πn/4)
A8)
Determine 2 possible positive values of Ø0, say, Ø1 and Ø2. Discuss if cos(Ø1t) or cos(Ø2t) will be obtained when passing through the DC converter.
A8) Taking T= 1/1000s
Cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000)
Ø1 is easily computed as 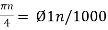
Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
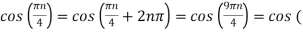 Ø2n/1000)
Ø2n/1000)
Ø2 = 2250π
Q9) For the following diagram explain whether it is even or odd.
A9)
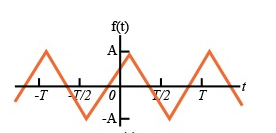
A9) The signal is neither even nor odd.
To make the signal even there is a slight shift to be applied as shown in the figure.
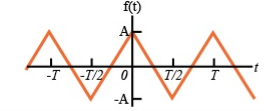
To make the signal odd
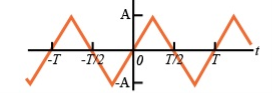
A periodic signal satisfying the condition
x(t) = -x (t ± T/2)
Is said to half symmetry. The Fourier series expansions of such type of periodic signals contains odd harmonics only.
Q10) Show that the signal x(t) that satisfies half wave symmetry contains Fourier coefficients with odd harmonics only.
A10)
A signal with half-wave symmetry that satisfies the condition x(t+T/2) = - x(t)
The Fourier coefficients of the signal are
Cn = 1/T 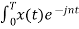 Ω0 dt
Ω0 dt
= 1/T [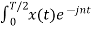 Ω0 dt +
Ω0 dt + 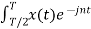 Ω0 dt
Ω0 dt
= 1/T 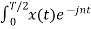 Ω0 dt +
Ω0 dt + 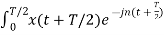 Ω0 dt
Ω0 dt
=  Ω0 dt -
Ω0 dt - 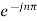
 Ω0 dt
Ω0 dt
Here e-jnπ = 1 for n
Even.
Hence Cn=0
Ω0 = 2π/T
Q11) Compute the Exponential series of the following series.
A11)
The time period of the signal x(t) isT=4.
A11) For our convenience let us choose one period signal from t= -1 to t=3
That is t0=-1 and t0+ T =3.
The fundamental frequency
 = 2 π/T =2 π/4= π/2.
= 2 π/T =2 π/4= π/2.
x(t) = {1 for -1 ≤t ≤1
-1 for 1≤t≤3}
a0= 1/T 
= ¼ 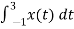 = ¼ [
= ¼ [ 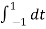 +
+ 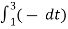 ]
]
= ¼ [ t |-1 1 + (-t) | 1 3]
= ¼ [ 1 – (-1) – (3-1)] = 0
a0 = 0.
An = 2/T 
½ 
= ½ 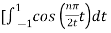 +
+ 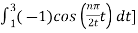
= ½ [ 2/ nπ sin(nπ/2t) | -1 1 - 2/nπ sin(nπ/2t) |1 3
= ½ [ 8/nπ sin(nπ/2)] = 4/nπ sin(nπ/2)
An=4/nπ sin(nπ/2)
Bn = 1/2 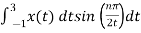
= ½ 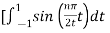 +
+ 
= ½ [ -2 /nπ cos(nπ/2t) | -1 1 + 2/nπ cos(nπ/2t) | 1 3
= -2/nπ(cos nπ/2 – cos nπ/2) + 2/nπ (cos 3nπ/2 – cos nπ/2)
= 0
Therefore 4/nπ sin nπ/2 = {0 n even
4/nπ = 1,9,13….
4/nπ 3,7,11,15…….
x(t) = 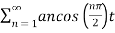
= 4/π cos (π/2 t) – 4/3π cos (3π/2 t) + 4/5π cos (5π/2 t) - ………….
= 4/π [ cos (π/2 t) -1/ 3 cos (3π/2 t) + 1/5 cos (5 π/2 t) – 1/7 cos (7π/2 t) + ……….
Q12) Find the Fourier integral of
A12)
f(x) = |sin x| |x| ≤ π
= 0 |x| ≥ π
Deduce that  π +1/ 1 - 2 cos (π/2) d = π/2
π +1/ 1 - 2 cos (π/2) d = π/2
A12)
f(x) = 2/π 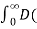

=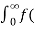 t
t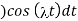 =
= 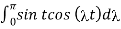
=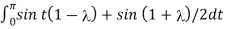
= - cost(1-) ]0 π - cost(1+) ]0 π
2(1-) 2(1+)
= 1/ 1- 2 [cos π + 1]
=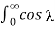 π +1/ 1 -2 cos (π/2) d = π/2
π +1/ 1 -2 cos (π/2) d = π/2
Q13) Find the Fourier Integral of
A13)
f(x) = 1 |x| ≤ 1
0 |x| ≥ 1
A13)
f(x) = 1/π 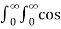 (t-x) dt d
(t-x) dt d
= 1/π 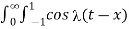 dt d
dt d
= 1/π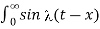 / ] -1 1 d
/ ] -1 1 d
= 1/π  -
- 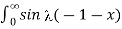 / d
/ d
= 1/π 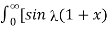 – sin
– sin 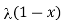 ]/ d
]/ d
= 2/π  / d = π/2 when |x| < 1 and 0 when |x| >1
/ d = π/2 when |x| < 1 and 0 when |x| >1
By setting x=0
= 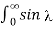 /
/  = π/2.
= π/2.
Q14) Consider the following signal set:
A14)
Find the convolution of above?
A14) By inspection, the signals can be expressed in terms of the following two basis functions:
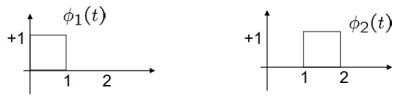
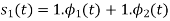

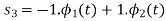


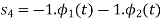
Note that the basis is orthogonal

Also note that each these functions have unit energy

We say that they form an orthonormal basis.
Q15) Consider an analog signal 
A15)
The frequency in the analog signal

The largest frequency is

The Nyquist rate is
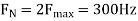
Q16) Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of X(t) = 1+ sin(2000πt) + cos (4000πt)
A16)
The frequencies are 0, 2000π and 4000π.
The Nyquist frequency is 4000π rad/s and the Nyquist rate is 8000π rad/s.
Q17) The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].
A17)
We know,
X[n] =x(nT)
= cos(200πnT)
= cos(2πn/3), where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
Q18) Explain Sampling Theorem?
A18)
In sampling the signal m(t) is multiplied with periodic pulse train. Let M(ω) the spectrum of the input signal be band limited with the maximum frequency of fm as shown in figure 1.
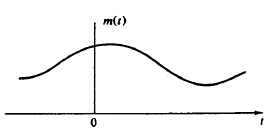
Figure: Spectrum of input Signal
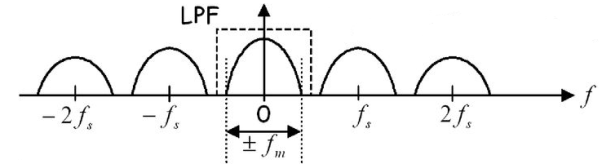
Figure: (fs>2 fm)
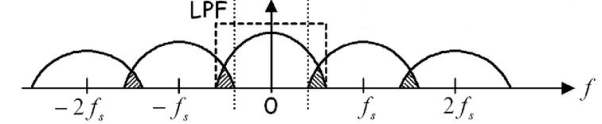
Figure: (fs<2 fm)
The frequency spectrum of this signal when impulse sampled is plotted in figure 2 (for fs>2 fm). In figure 3 for (fs<2 fm). From figure 2 and figure 3 we can conclude that as long as fs≥2fm the original signal is preserved in the sampled signal and can be extracted from it by the low pass filter. This is known as Shannon’s Sampling theorem. This theorem states that the information contained in a signal is fully preserved in the sampled form as long as the sampling frequency is at least twice the maximum frequency contained in the signal.
Q19) Define energy and power in a signal?
A19)
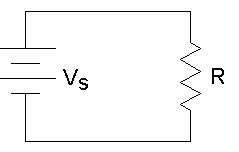
A19) The power for above circuit with R=1Ω is given as
P= 
For R=1Ω
P=V2(t)=I2(t)
This is known as normalized power.
Total energy E=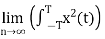 dt Joules
dt Joules
E=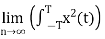
Energy of periodic signal is always infinite.
Now calculating power P=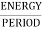
P=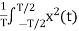 dt
dt
P=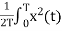 dt Watts
dt Watts
Power for Non-periodic signal is always zero.
Q20) List all properties of Fourier transform?
A20)
Properties of Fourier Transform
Linear Property
If x(t) -> X(w)
Y(t) -> Y(w) then
a x(t) + b y(t) -> a X(w) +b Y(w)
Time Shifting Property
If x(t)⟷F. TX(ω)
Then Time shifting property states that
x(t−t0) ⟷F. T e−jω0t X(ω)
Frequency Shifting Property
If x(t)⟷X(ω)
Then frequency shifting property states that
Ejω0t.x(t)⟷X(ω−ω0)
Time Reversal Property
If x(t)⟷X(ω)
Then Time reversal property states that
x(−t) ⟷X(−ω)
Differentiation Property
If x(t)⟷X(ω)
Then Differentiation property states that
Dx(t)dt⟷jω.X(ω)
dnx(t)dtn⟷(jω) n.X(ω)
Integration Property
Integration property states that
∫x(t)dt⟷1jω X(ω)
Then
∭...∫x(t)dt⟷(jω) n X(ω)
Multiplication and Convolution Properties
If x(t)⟷X(ω)
y(t)⟷Y(ω)
Then multiplication property states that
x(t). y(t)⟷X(ω)∗Y(ω)
And convolution property states that
x(t)∗y(t)⟷1/2πX(ω). Y(ω)