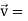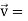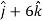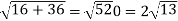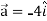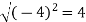Unit-3

Vector differential calculus

Q1: A particle moves along the curve 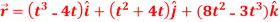, here ‘t’  is the time. Find its velocity and acceleration at t = 2.

A1:

Here we have-

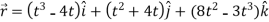
Then, velocity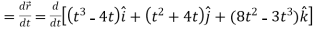

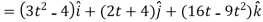
Velocity at t = 2,

                                  =

Acceleration =

Acceleration at t = 2,

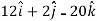
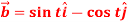Q2: If and then find-

1.

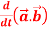
2.

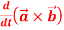
A2:

We know that-

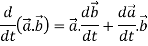
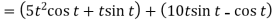
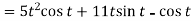
2.

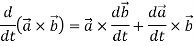
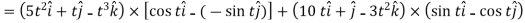
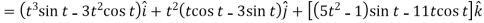
Q3: A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. then find the velocity and acceleration at time t = 0 and t = π/2.

And find the magnitudes of the velocity and acceleration at time t.

A3:

suppose

Now,

Again acceleration-

Now-

Q4: Define scalar point function and vector point function.

A4:

Scalar point function-

If for each point P of a region R, there corresponds a scalar denoted by f(P), in that case f is called scalar point function of the region R.

Note-

Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).

Vector point function-

If for each point P of a region R, then there corresponds a vector then is called a vector point function for the region R.

Q5: A object move in the path where t is the time in seconds and distance is measured in feets.

Then find and as functions of t.

A5:

We know that-

And

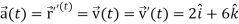
Now we will use-

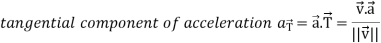
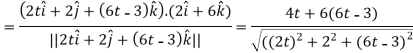
And now-

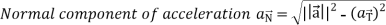
Q6: If , then show that

A6:

Suppose   and

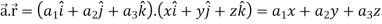
Now taking L.H.S,

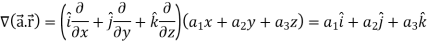
Which is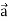

Hence proved.

Q7: If 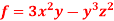then find grad f at the point (1,-2,-1).

A7:

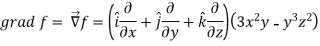
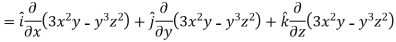
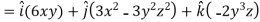
Now grad f at (1 , -2, -1) will be-       

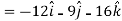
Q8: Show that-

1.

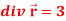
2.

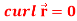
A8:
We know that-

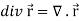
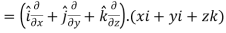
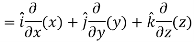
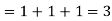
2. We know that-

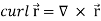
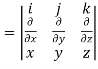
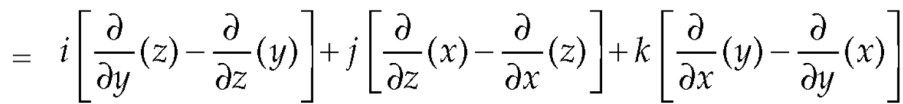
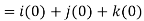= 0

Q9: If 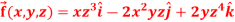then find the divergence and curl of .

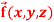A9:
we know that-

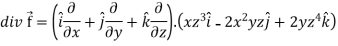
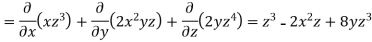
Now-

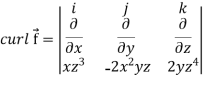
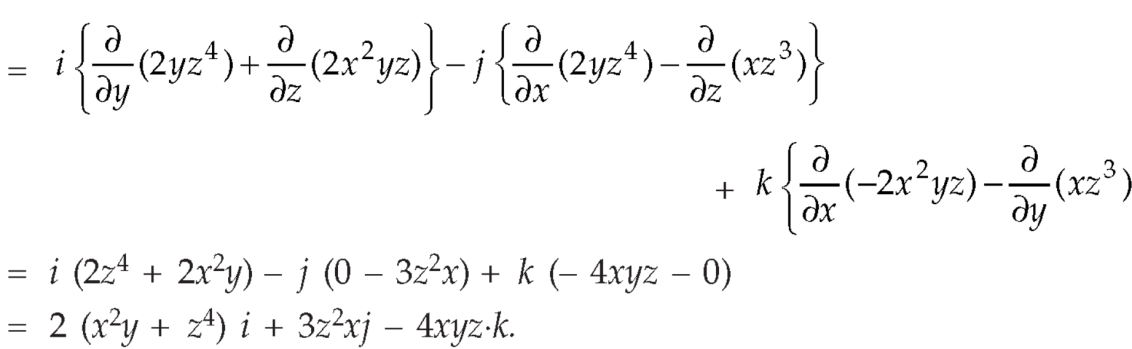
Q10: If 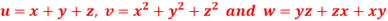then prove that grad u , grad v and grad w are coplanar.

A10:
 

Here-                     

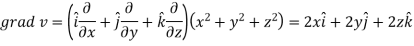
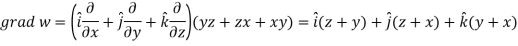
Now-

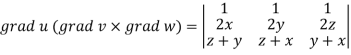
Apply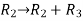

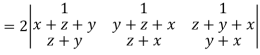
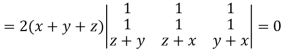
Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.