Unit-5
Fourier series
Q1: Find the fourier series of the function f(x) = x where 0 < x < 2 π
A1:
We know that, from fourier series,
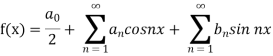
First we will find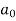 
,
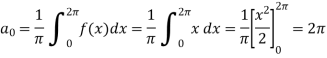
Now,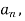 
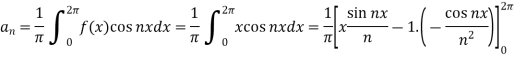
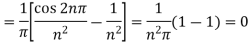
And 
,
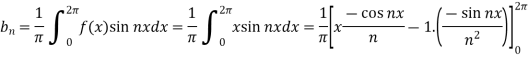
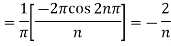
Put these value in Fourier series, we get
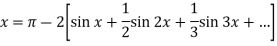
Q2: Find the Fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
A2:
First we will find
= 
=
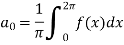
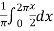
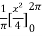
= π
= π
Similarly,
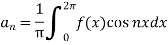
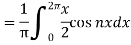
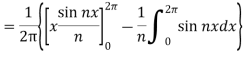
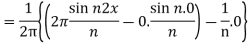
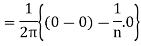
Which gives,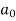 
= 0
Now,
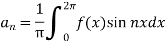
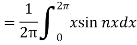
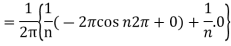
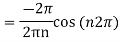
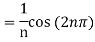
We get,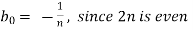 
We know that, the Fourier series
Put these values in Fourier series, we get
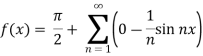
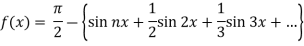
Q3: Find the Fourier series for f(x) =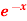 
in the interval 
.
A3:
Suppose
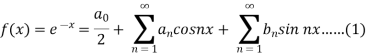
Then-
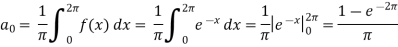
And
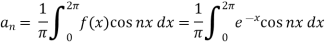
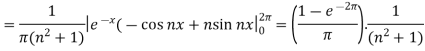
So that-
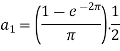
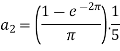
And then-
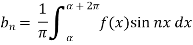
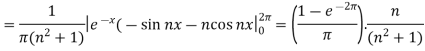
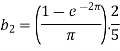
Now put these value in equations (1), we get-
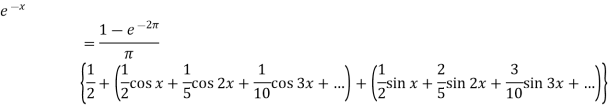
Q4: Find the fourier series of the function f(x) = x where 0 < x < 2 π
A4:
We know that, from fourier series,
f(x) =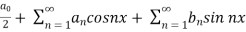 
first we will find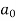 
,
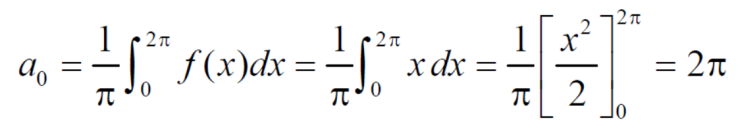
Now, 
And 
,
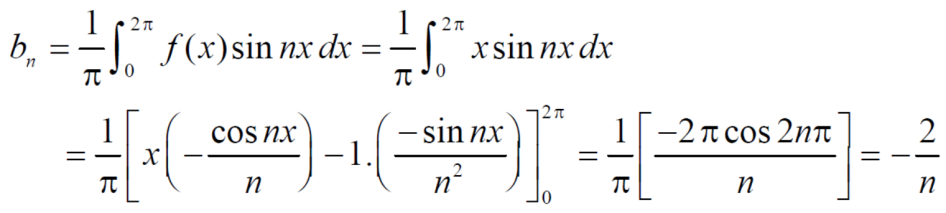
Put these value in fourier series, we get
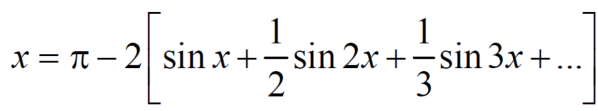
Q5: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
A5:
First we will find
= 
= 
=
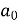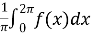
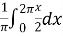
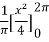
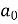= π
= π
Similarly,
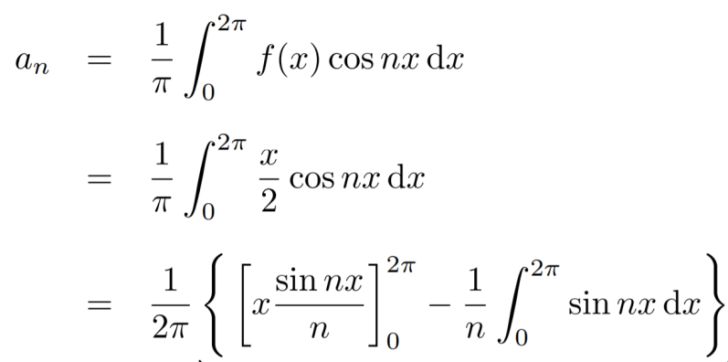
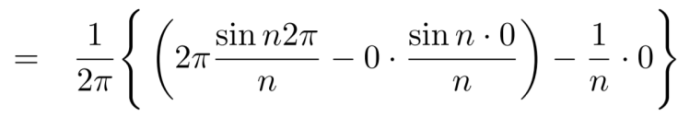
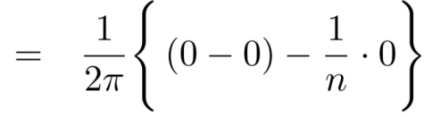
Which gives,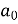 
= 0
Now,
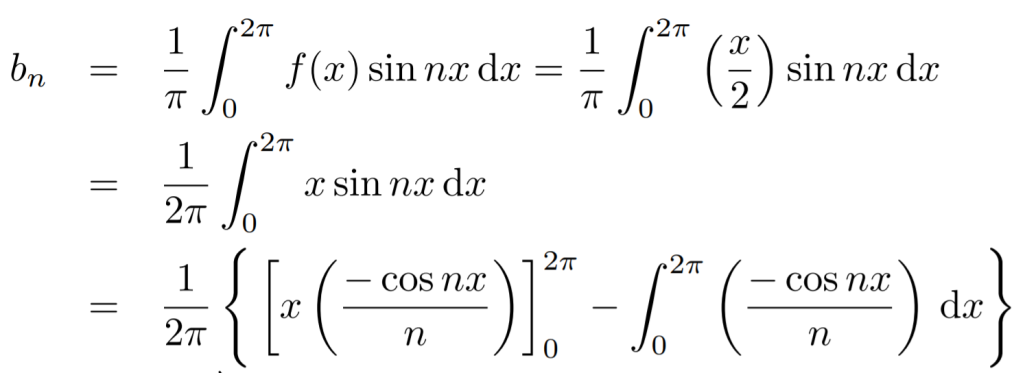
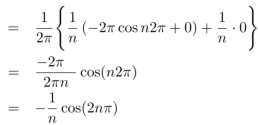
We get,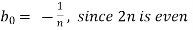 
We know that, the fourier series
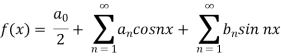
Put these values in fourier series, we get
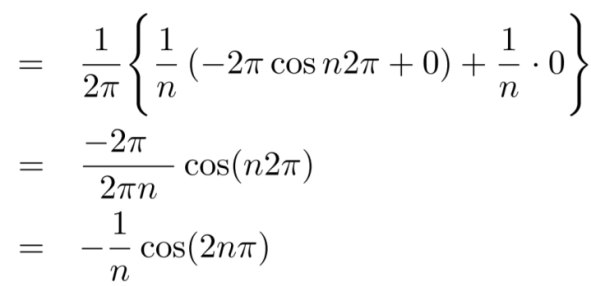
Q6: Find the Fourier series for f(x) =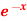 
in the interval 
.
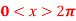A6:
Suppose
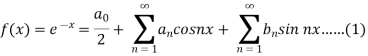
Then-
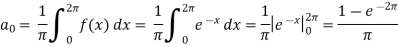
And
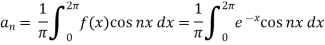
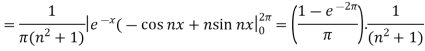
So that-
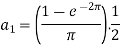
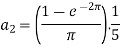
And then-
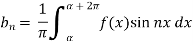
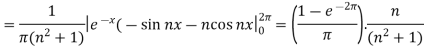
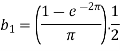
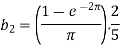
Now put these value in equations (1), we get-
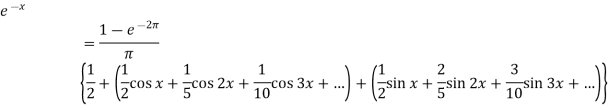
Q7: Find the fourier expression of f(x) = x³ for –π< x <π.
A7:
Here, we can see that f(x) Is an odd function
So that,
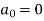and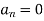
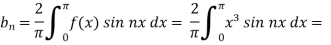
We will use here ,
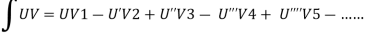
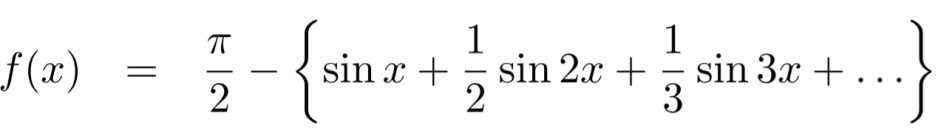
We get the value of f(x),
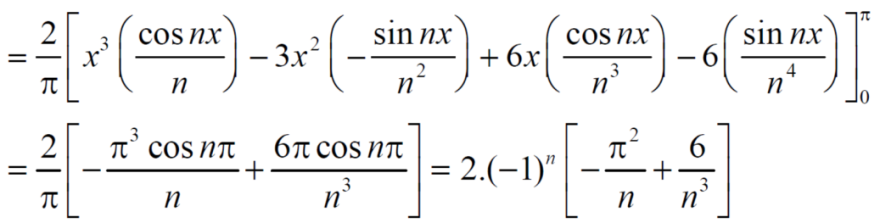
Q8: Find a Fourier series for
; 
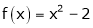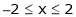
A8:
Here
; 
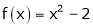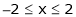
Since f(x) is even function hence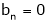 
It’s Fourier series is
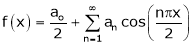… (1)
Where
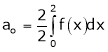
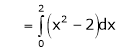
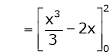
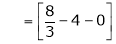
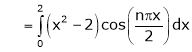
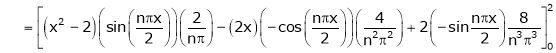
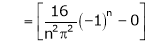
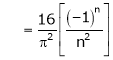
Hence equation (1) becomes,
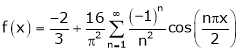
Q9: Find the Fourier sine series for the function-
Where ‘a’ is a constant.
A9:
here we know-
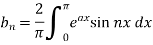
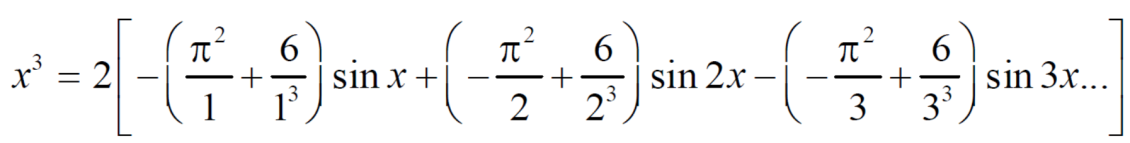
We know that-
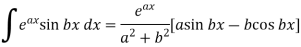
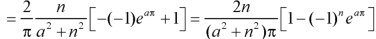
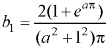
And
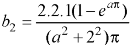
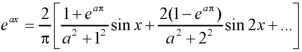
Q10: Using complex form,find the Fourier series of the function
f(x) = sinx =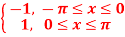 
A10:
We calculate the coefficients 
= 
=
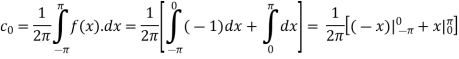
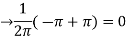
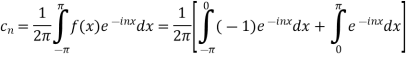
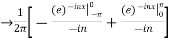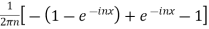
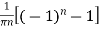
Hence the Fourier series of the function in complex form is
We can transform the series and write it in the real form by renaming as
n=2k-1,n=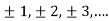
= 
