Unit 3

LASER AND FIBRE OPTICS

Q1) Differentiate between spontaneous and stimulated emissions.

Solution:

Q2) Discuss Einstein’s theory of interaction of electromagnetic radiation with matter?

Solution: Let us discuss Einstein’s theory of interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in following three steps.

Stimulated  Absorption:

Let E1 and E2be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2interacts with an atom present in the ground state, the atom gets excitation form ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.

Stimulated absorption rate ∝ Number of atoms in the ground state

∝   Density of photons Spontaneous emission

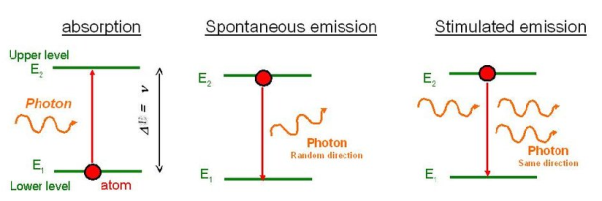
Spontaneous Emission:

Let E1and E2be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. The excited atom does not stay in a long time in the excited state. The excited atom gets de-excitation after its life time by emitting a photon of energy hν= E1−E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to ground state by its own so it is named as spontaneous emission.

The spontaneous emission rate depends up on the number of atoms present in the excited state.

Spontaneous emission ∝rate number of atoms in the excited state

Stimulated Emission:

This phenomena is responsible for producing laser light. Let E1and E2be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. Let, a photon of energy hν= E1−E2interacts with the excited atom with in their life time; the atom gets de-excitation to ground state by emitting of another photon. These photons have same phase and it follows coherence. This phenomenon is called stimulated emission.

Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.

Stimulated emission rate ∝ number of atoms in the excited state

∝ Density of photons

Q3) Calculate the wavelength of radiation emitted by an LED made up of a semiconducting material with band gap energy 2.8eV.

Solution:

E = hc/ʎ
Therefore, ʎ = hc/E
ʎ = 4430.8 Å.

Q4) Calculate the number of photons, from green light of mercury (ʎ = 4961 Å), required to do one joule of work.

Solution:

E = hc/ʎ
E = 4.006×10-19 Joules
Number of photons required = (1 Joule)/(4.006×10-19)
N = 2.4961×1018/m3.

Q5) Derive Einstein’s coefficient A and B ?

Solution: The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1be the number of atoms per unit volume with energyE1and N2be the number of atoms per unit volume with energyE2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2.

Then, the energy density of photons ρ(υ) =nhυ

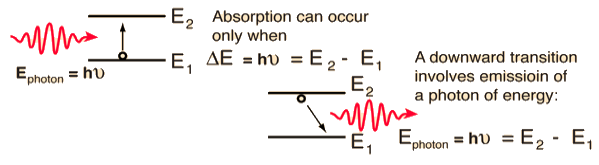
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs.

At the equilibrium the upward transitions must be equal downward transitions.

Upward Transition

Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.

We have seen above that

Stimulated absorption rate∝  N1i.e. Number of atoms in the ground state

∝ ρ(υ)i.e. Density of photons spontaneous emission

Stimulated absorption rate= B12N1ρ(υ)  ………(1)

Where B12is the Einstein coefficient of stimulated absorption.

Downward transition

The spontaneous emission rate depends up on the number of atoms present in the excited state.

Spontaneous emission rate∝   N2 i.e. number of atoms in the excited state

Spontaneous emission rate  = A21N2  ………(2)

Where A21 is the Einstein coefficient of spontaneous emission.

Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.

Stimulated emission rate ∝N2 i.e. number of atoms in the excited state

∝ρ(υ) i.e. Density of photons

Stimulated emission rate = B21N2ρ(υ)  ………(3)

If the system is in equilibrium the upward transitions must be equal downward transitions.

upward transitions =downward transitions

B12N1ρ(υ) = A21N2+B21N2ρ(υ)   ………(4)

B12N1ρ(υ) -B21N2ρ(υ) = A21N2

(B12N1-B21N2)ρ(υ) = A21N2

ρ(υ) =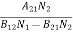   ………(5)

Divide with B21N2 in numerator and denominator in right side of the above equation,

ρ(υ)  =  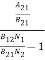=     ………(6)

ρ(υ)  =  = =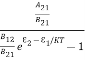   ………(7)

We know from Maxwell Boltzmann distribution law

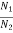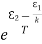=    ………(8)

 And also from Planck’s law, the radiation density

ρ(υ) =    ………(9)

Comparing the two equations (7) and (9)

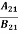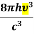=    and 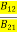=1  ………(10)

The above relations referred to as Einstein relations.

From the above equation for non degenerate energy levels the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.

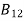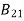=   ………(11)

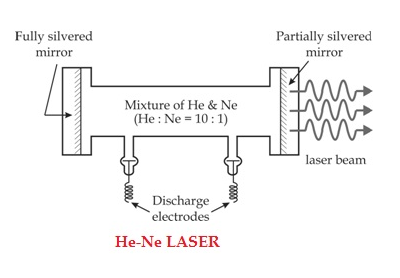
Q6) What is the relationship between B21 and B12?
a) B12> B21
b) B12< B21
c) B12 = B21
d) No specific relation

Solution: C is the correct answer.

B21 is the coefficient for the stimulated emission while B12 is the coefficient for stimulated absorption. Both the processes are mutually reverse processes and their probabilities are equal. Therefore, B12 = B21.

Q7) Discuss construction, working and application of gasLaser?

Or

Discuss construction, working and application of He-Ne Laser?

Or

Discuss four level laser ?

Solution: He-Ne Laser

The first He-Ne gas laser was fabricated in 1961 by Ali Javan, Bennett and Herriott at Bell Telephone Laboratories. others. Helium-Neon laser is a type of gas laser in which a mixture of helium and neon gas is used as a gain medium. Helium-Neon laser is also known as He-Ne laser. The helium-neon laser was the first continuous wave laser ever constructed. The helium-neon laser operates at a wavelength of 632.8 nanometres (nm), in the red portion of the visible spectrum.

Ruby laser is a pulse laser, even it have high intense output. For continuous laser beam gas lasers are used. Using gas lasers, we can achieve highly coherence, high directionality and high monochromacity beam. The output power of the gas laser is generally in few milliwatts.

Construction

The helium-neon laser consists of three essential components:

Pump source

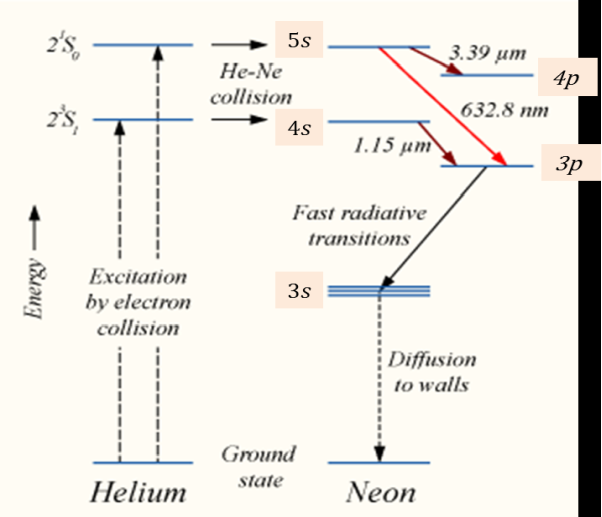
The gain medium of a helium-neon laser is made up of the mixture of helium and neon gas contained in a glass tube at low pressure. In He-Ne gas laser, the He and Ne gases are taken in the ratio 10:1 in the discharge tube.

Gain medium

In He-Ne laser 80cm length and 1cm diameter discharge is generally used. The out power of these lasers depends on the length of the discharge tube and pressure of the gas mixture. Therefore, in order to achieve population inversion, we need to pump electrons from lower energy state of the helium.In He-Ne laser, neon atoms are the active centres and have energy levels suitable for laser transitions while helium atoms help in exciting neon atoms.

Resonating cavity

Two reflecting mirrors are fixed on either ends of the discharge tube, in that, one is partially reflecting and the other is fully reflecting. The fully silvered mirror will completely reflect the light whereas the partially silvered mirror will reflect most part of the light but allows some part of the light to produce the laser beam.

Working

When the electric discharge is passing through the gas mixture, the electrons accelerated towards the positive electrode. During their passage, they collide with He atoms and excite them into higher levels. 23s1 and 21s0 form ground state of He atom. In higher levels 23s1 and 21s0, the life time of He atoms is more. So there is a maximum possibility of energy transfer between He and Ne atoms through atomic collisions. When He atoms present in the levels 23s1 and 21s0collide with Ne atoms present ground state, the Ne atoms gets excitation into higher levels 4s and 5s.

Due to the continuous excitation of Ne atoms, we can achieve the population inversion between the higher levels 4s and 5s and lower levels 3p and 4p. The various transitions5s to 4p,4s to 3p and 5s to 3p leads to the emission of wavelengths  3.93μm, 1.51μm and 6328 Å or 632.8μm.

The first two corresponding to the infrared region while the last wavelength is corresponding to the visible region. The Ne atoms present in the 4s level are de-excited into 3s level, by spontaneously emitting a photon of around wavelength 6000 Å. When a narrow discharge tube is used, the Ne atoms present in the level 3s collide with the walls of the tube and get de-excited to ground state energy level.

Advantages of helium-neon laser

Disadvantages of helium-neon laser

Applications of helium-neon lasers

Q8) Discuss construction, working and application of Solid-State Laser?

Or

Discuss construction, working and application of Ruby Laser?

Or

Discuss three level laser ?

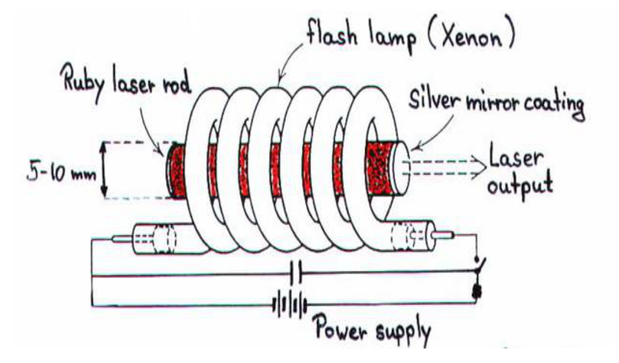
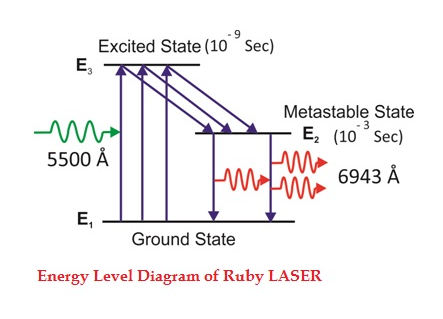
Solution: Ruby laser

Ruby laser is a three level solid state laser and was constructed by Maiman in 1960. Ruby laser is one of the few solid-state lasers that produce visible light. It emits deep red light of wavelength 694.3 nm.

Construction

A ruby laser consists of three important elements: laser medium, the pump source and the optical resonator.

Laser Medium

Ruby (Al2O3+Cr2O3) is a crystal of Aluminium oxide, in which 0.05% of Al+3 ions are replaced by the Cr+3 ions. The colour of the rod is pink. The active medium or laser medium in the ruby rod is Cr+3 ions.In ruby laser 4cm length and 5mm diameter rod is generally used. The ruby has good thermal properties.

The pump source

The ruby rod is surrounded by xenon flash tube, which provides the pumping light to excite the chromium ions in to upper energy levels. The ruby rod was surrounded by a helical xenon flash lamp.

We know that population inversion is required to achieve laser emission. Population inversion is the process of achieving the greater population of higher energy state than the lower energy state. In order to achieve population inversion, we need to supply energy to the laser medium i.e. to ruby crystal.

Xenon flash tube emits thousands joules of energy in few milliseconds, but only a part of that energy is utilized by the chromium ions while the rest energy heats up the apparatus. A cooling arrangement is provided to keep the experimental set up at normal temperatures.

Optical resonator

Both the ends of the rods are highly polished and made strictly parallel. The ends are silvered in such a way, one becomes partially reflected the laser beam was emitted through that end and the other end fully reflected to reflect all the rays of light striking it.

Working of ruby laser:

Consider a ruby laser medium consisting of three energy levels E1, E2, E3with N number of electrons.

We assume that the energy levels will be E1< E2< E3. The energy level E1 is known as ground state or lower energy state, the energy level E2 is known as metastable state, and the energy level E3 is known as pump state.

Let us assume that initially most of the electrons are in the lower energy state (E1) and only a tiny number of electrons are in the excited states (E2 and E3).

The energy level diagram of chromium ions is shown in figure. The chromium ions get excitation into higher energy levels by absorbing of 5500Åof wavelength radiation. The excited chromium ions stay in the level E3 for short interval of time (10-8 to 10-9 Sec). After their life time most of the chromium ions are de-excited from E3 to E1 and a few chromium ions are de-excited from E3 to E2.

The transition between E3 and E2 is non-radioactive transition i.e. the chromium ions gives their energy to the lattice in the form of heat. In the Meta stable state the life time of chromium ions is 10-3 sec. The life time of chromium ions in the Meta stable state is 105 times greater than the life time of chromium ions in higher state.

Due to the continuous working of flash lamp, the chromium ions are excited to higher state E3 and returned to E2 level. After few milliseconds the level E2 is more populated than the level E1 and hence the desired population inversion is achieved. The state of population inversion is not a stable one. The process of spontaneous transition is very high. When the excited chromium ion passes spontaneously from E3 to E2it emits one photon of wave length 6943 Å. The photon reflects back and forth by the silver ends and until it stimulates an excited chromium ion in E2 state and it to emit fresh photon in phase with the earlier photon. The process is repeated again and again until the laser beam intensity is reached to a sufficient value. When the photon beam becomes sufficient intense, it emerges through the partially silvered end of the rod. The wave length 6943 Å is in the red region of the visible spectrum.

Draw backs of ruby laser

Application of ruby laser

Q9) How laser light get amplify by population inversion ?

Solution: Population inversion

Definition

The number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.

Population inversion as name suggests that this is inverted phenomena. In general lower energy level is more populated that means it have more number of atoms in lower energy level as compared to higher energy level. But by pumping we will obtain a state when the number of atoms present in the higher energy state is greater than the number of atoms present in lower energy state.

Let us consider two level energy system of energies E1 and E2 as shown in figure.

Let N1 and N2 be the populations that means number of atoms per unit volume of energy levels E1 andE2 respectively.

According to Boltzmann’s distribution the population of an energy level E, at temperature T is given by

Ni=N0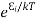  

Where N0 is the population of the lower level or ground state and k is the Boltzmann’s constant.

From the above relation, the population of energy levels E1 andE2  are

N1=N0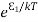 

N2=N0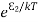 

At ordinary conditionsN1>N2 i.e., the population in the ground or lower state is always greater than the population in the excited or higher states. The stage of making, population of higher energy level is greater than the population of lower energy level is called population inversion i.e. N1< N2

When population inversion method is used to enforce more and more atoms to give up photons. This initiates a chain reaction and releasing massive amount of energy.

This results in rapid build-up of energy of emitting one particular wavelength traveling coherently in fixed direction. This process is called amplification by stimulated emission using population inversion.

This population inversion situation is essential for a laser action. For any stimulated emission, It is necessary that the upper energy level or meta stable state should have a long life time, i.e., the atoms should pause at the meta stable state for more time than at the lower level.

Q10) What is Pumping?  Discuss various type of pumping mechanisms?

Solution: For laser action, pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.

A system in which population inversion is achieved is called as an active system. The method of raising the particles from lower energy state to higher energy state is called pumping.

The process of achieving of population inversion is called pumping.

This can be done by number of ways.

The most commonly used pumping methods are

Optical pumpingAs the name suggests, in this method, light is used to supply energy to the laser medium. Optical pumping is used in solid laser. Xenon flash tubes are used for optical pumping. Since these materials have very broad band absorption, sufficient amount of energy is absorbed from the emission band of flash lamp and population inversion is created.So xenon flash lamp is used to produce more electrons in the higher energy level of the laser medium.

Examples of optically pumped lasers are ruby, Nd: YAG Laser(Neodymium: Yttrium Aluminum Garnet).

Electrical discharge pumping Electrical discharge pumping is used in gas lasers. Since gas lasers have very narrow absorption band pumping then any flash lamp is not possible.Electric discharge refers to flow of electrons or electric current through a gas, liquid or solid.

In this method of pumping, electric discharge acts as the pump source or energy source. A high voltage electric discharge (flow of electrons, electric charge, or electric current) is passed through the laser medium or gas. The intense electric field accelerates the electrons to high speeds and they collide with neutral atoms in the gas. As a result, the electrons in the lower energy state gains sufficient energy from external electrons and jumps into the higher energy state

Examples of Electrical discharge pumped lasers are He-Ne laser, CO2 laser, argon-ion laser etc.

Chemical pumpingChemical reaction may also result in excitation and hence creation of population inversion in few systems.

If an atom or a molecule is produced through some chemical reaction and remains in an excited state at the time of production, then it can be used for pumping. The hydrogen fluoride molecule is produced in an excited state when hydrogen and fluorine gas chemically combine. The number of produced excited atoms or molecules is greater than the number of normal state atoms or molecules. Thus, population inversion is achieved.

Examples H2 + F2→ 2HF, in this chemical reaction, hydrogen (H2) and fluorine (F2) molecules are chemically combined to produce hydrogen fluoride molecule (2HF) in an excited state.

Thermal Pumping: Sometimes we can achieve population inversion by heating the laser medium. In thermal pumping, heat acts as the pump source or energy source. In this method, population inversion is achieved by supplying heat into the laser medium.

When heat energy is supplied to the laser medium, the lower energy state electrons gains sufficient energy and jumps into the higher energy level.

The process of achieving population inversion in thermal pumping is almost similar to the optical pumping or electric discharge method, except that in this method heat is used as pump source instead of light or electric discharge.

Injection current pumpingIn semiconductors, injection of current through the junction results in creates of population inversion among the minority charge carriers.

Examples of such systems are InP and GaAs.

Inelastic Atom-Atom Collisions: Like the electric discharge method, here also a high voltage electric discharge acts as a pump source. However, in this method, a combination of two types of gases, say X and Y are used. The excited state of gas X is represented as X+ whereas gas Y is represented as Y+. Both X and Y gases have the same excited states (X+ and Y+).

When high voltage electric discharge passes through a laser medium having two types of gases X and Y, the lower energy state electrons in gas X will move to the excited state X+ similarly the lower energy state electrons in gas Y moves to the excited state Y+.

Initially, during electric discharge, the lower energy state electrons in gas X or atom X gets excited to X+ due to continuous collision with electrons. The excited state electrons in gas X+ now collide with the lower energy state electrons in gas Y. As a result, the lower energy state electrons in gas Y gains sufficient energy and jump into the excited state Y+. This method is used in the Helium–Neon (He-Ne) laser.

Q11) Why Two-level laser is not possible? Give valid reason.

Solution:

Consider a group of electrons with two energy levels E1 and E2.

E1 is the lower energy state and E2 is the higher energy state.
N1 is the number of electrons in the energy state E1.
N2 is the number of electrons in the energy state E2.
The number of electrons per unit volume in an energy state is the population of that energy state.

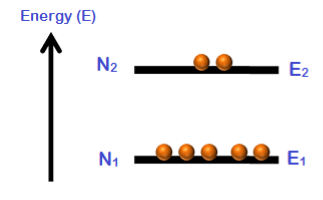
Population inversion cannot be achieved in a two energy level system. Under normal conditions, the number of electrons (N1) in the lower energy state (E1) is always greater as compared to the number of electrons (N2) in the higher energy state (E2).

N1 > N2

When temperature increases, the population of higher energy state (N2) also increases. However, the population of higher energy state (N2) will never exceeds the population of lower energy state (N1).

At best an equal population of the two states can be achieved which results in no optical gain.

N1 = N2

Two energy level lasers are not possible. We can notget population inversion in a 2 level LASER no matter how much we pump the atoms in the ground state. And since population inversion is a necessity for lasing action, we don't have two level lasers.

Therefore, we need 3 or more energy states to achieve population inversion. The greater is the number of energy states the greater is the optical gain.

There are certain substances in which the electrons once excited; they remain in the higher energy level or excited state for longer period. Such systems are called active systems or active media which are generally mixture of different elements.

When such mixtures are formed, their electronic energy levels are modified and some of them acquire special properties. Such types of materials are used to form 3-level laser or 4-level laser.

Q12) Write a note on Reciprocal Lattice ?

Solution: Reciprocal Lattice

The fundamental property of a crystal is its triple periodicity and a Crystal may be generated by repeating a certain unit of pattern through the translations of a certain lattice called the direct lattice. The macroscopic geometric properties of a crystal are a direct consequence of the existence of this lattice on a microscopic scale. Let us for instance consider the natural faces of a crystal. These faces are parallel to sets of lattice planes. The lateral extension of these faces depends on the local physiochemical conditions during g-growth but not on the geometric properties of the lattice.

To describe the morphology of a crystal, the simplest way is to associate, with each set of lattice planes parallel to a natural face, a vector drawn from a given origin and normal to the corresponding lattice planes. To complete the description it suffices to give to each vector a length directly related to the spacing of the lattice planes. This polar diagram is the geometric basis for the reciprocal lattice.

On the other hand, the basic tool to study a crystal is the diffraction of a wave with a wavelength of the same order of magnitude as that of the lattice spacing. The nature of the diffraction pattern is governed by the triple periodicity and the positions of the diffraction spots depend directly on the properties of the lattice.

This operation transforms the direct space into an associated space, the reciprocal space, and the diffraction spots of a crystal are associated with the nodes of its reciprocal lattice. The reciprocal lattice is therefore an essential concept for the study of crystal lattices and their diffraction properties. This concept and the relation of the direct and reciprocal lattices through the Fourier transform was first introduced in crystallography by P. P. Ewald (.1921).

Every crystal structure has two lattices associated with it, the crystal lattice and the reciprocal lattice. A diffraction pattern of a crystal is the map of the reciprocal lattice of the crystal and a microscope structure is the map of the crystal structure. If a1, a2, a3 are the axis vectors of the real lattice, and b1, b2, b3 are the axis vectors of the reciprocal lattice, they are related by the following equations:

Using b1, b2, b3 as a basis for a new lattice, then the vectors are given by

G=n1b1+n2b2+n3b3

Figure 31 illustrates the 1-D, 2-D and 3-D real crystal lattices and its corresponding reciprocal lattices.

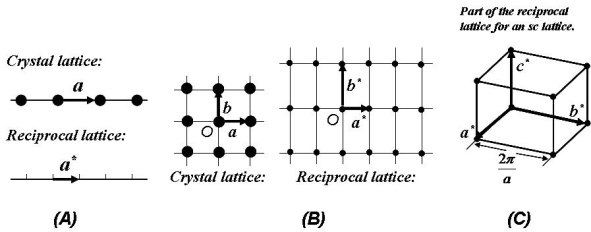
Figure 31: (a). Reciprocal lattice for a 1-D crystal lattice; (b).Reciprocal lattice for a 2-D crystal lattice; (c). Part of the reciprocal lattice for ansc lattice.

Based on the definition of the reciprocal lattice, the vectors of the reciprocal lattice can be related the crystal planes of the direct lattice:

(a) The vector Ghklis normal to the (hkl) crystal planes.

(b) The interplane distance dhkl is related to the magnitude of Ghkl by

dhkl=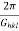

The main features of the reciprocal lattice are:

Q13) Define the term Space Lattice?

Solution: In a solid crystalline material, the atoms or molecules are arranged regularly and periodically in all three dimensions. The atomic arrangement in a crystal is called crystal structure.

To explain crystal symmetries easily, it is convenient to represent an atom or a group of atoms that repeats in three dimensions in the crystal as a unit.If each such atom or unit of atoms in a crystal is replaced by a point in space, then the resultant points in space are called space lattice.

Each point in a space lattice is called a lattice point.Each atom or unit of atoms is called basis or pattern.

A space lattice represents the geometrical pattern of crystal in which the surroundings of each lattice point is the same. If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.

On the other hand, if the atom or the atoms at lattice points are not same, then it is said to be a non-Bravais lattice.

A space lattice or crystal lattice is defined as three dimensional infinite arrays of points in space in which every point has surroundings identical to that of every other point in the array.

Q14) Define Basis in Crystal Structure?

Solution: The atomic arrangement in a crystal is called crystal structure. The crystal structure is formed by associating every lattice point with an atom or an assembly of atoms or molecules or ions, which are identical in composition, arrangement and orientation, called the basis. i.e. an atom, or a group of atoms or molecules identical in composition is called the basis or the pattern.

The basis provides the number of atoms per lattice point, their types, mutual orientations and distances of separation between the atoms.

 If the basis is substituted for the lattice points, then the resulting structure is called crystal structure as shown in Figure.

lattice + basis = crystal structure.

The basis shown in Figure contains two different atoms. In copper and sodium crystals the basis is single atoms; In NaCl, the basis is diatomicand in CaF2the basis is triatomic. A lattice is an imaginary assumption while the crystalstructure is a realconcept.

1 Figure:  Lattice sites, Basis and crystal structure

Q15) What is Unit Cell and also discuss about Lattice Parameters?

Solution: Unit cell

Unit cell is small repeating entity of the atomic structure. It is the basic building block of the crystal structure. It defines the entire crystal structure with the atom positions within.

Unit cells for most of the crystals are parallelepipeds or cubes having three sets of parallel faces. A unit cell is the basic structural unit or building block of the crystal.

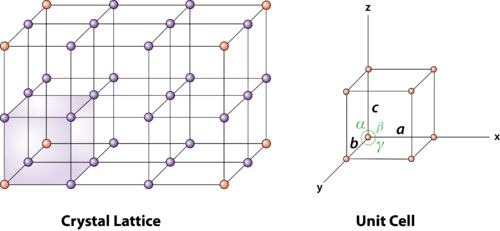
2 Figure: unit cell and unit cell parameter

A unit cell is defined as the smallest parallelepiped volume in the crystal, which on repetition along the crystallographic axes gives the actual crystal structure or the smallest geometric figure, which on repetition in three-dimensional space, gives the actual crystal structure is called a unit cell.

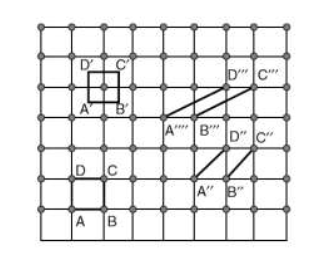
Choice of a unit cell is not unique but it can be constructed in a number of ways as shown in figure. Following figure shows different ways of representing unit cells in a two-dimensional lattice. A unit cell can be represented as ABCD or A′B′C′D′ or A′′B′′C′′D′′, etc.

 3 Figure: Construction of unit cell in different way

First we define crystallographic axes. These axes are obtained by the intersection of the three non-coplanar faces of the unit cell. The angles between these faces or crystallographic axes are known as interfacial or interaxial angles. The angles between the axes Y and Z is α, between Z and X is β and between X and Y is γ. The translational vectors or primitives a, b, c of a unit cell along X, Y, Z axes and interaxial angles α, β, γ are called Cell parameters. These cell parameters are shown in (Figure 2). The cell parameters determine the actual size and shape of the unit cell.

Q16) What do you meant by Primitive and non-primitive unit cells?

Solution: The unit cell formed by primitives is called a simple or a primitive unit cell. A primitive unit cell contains only one lattice point. If a unit cell contains more than one lattice point, then it is called a non-primitive unit cell or a multiple unit cell. Most of the unit cells of various crystal lattices contain two or more lattice points and hence it is not necessary that unit cell should be a primitive unit cell.

4 Figure: Primitive and non-primitive unit cells

Q17) What is the Difference between Crystalline solids and amorphous solids?

Solution:

Q18) Sketch the following planes of a cubic unit cell: (111) and (210)

Solution:

Intercepts: a ,a , a

Fractional intercepts: 1 , 1 , 1

Miller Indices: (111)

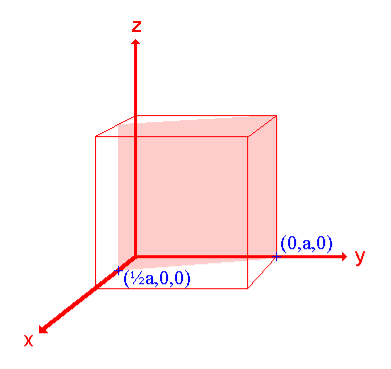
ii.            The (210) surface

Intercepts: ½a ,a ,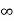

Fractional intercepts: ½ , 1 ,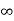

Miller Indices: (210)

Q19) Explain Bragg’s Law and its importance?

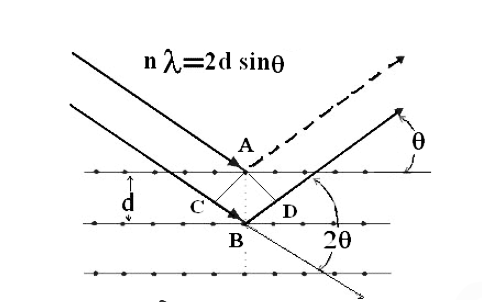
Solution: Consider a set of parallel planes called Bragg’s planes. Each atom is acting as a scattering center. The intensity of the reflected beam at certain angles will be maximum when the path difference between two reflected waves from two adjacent planes is an integral multiple of λ.

Let‘d’ be the distance between two adjacent planes, 'λ’ be the wavelength of the incident x-ray, ‘θ’ be the glancing angle.

The path difference between the rays reflected at A & B is given by

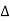=CB + BD= d sinθ + d sinθ = 2dsinθ

If the two consecutive planes scatter waves in phase with each other, then the path difference must be an integral multiple of wavelength. 

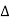=nλ

For the reflected light intensity to be maximum, the path difference

nλ= 2dsinθ

Where ‘n’ is the order of scattering.

This is called Bragg’s law

Therefore, Bragg’s law states that X-rays diffracted from different parallel planes of a crystal interfere constructively when the path difference is integral multiples of wavelength of X-rays.

From Bragg’s lawnλ = 2d sin θ, since maximum possible value for sin θ is 1,

nλ/2d≤ 1 or λ≤ 2d.

This sets the limitation on the wavelength, i.e. in order to get the diffraction pattern by a crystal, the wavelength of X-rays should not exceed twice the inter-planar spacing.

Importance of Bragg’s law:

1.Bragg’s law is the essential condition to be satisfied by crystal planes in order to get diffraction pattern from a crystal.

2.It is used to calculate inter-planar spacing. Knowing the values of inter-planar spacing, lattice parameters can be determined.

Q20) In a diffractometer, X-rays with a wavelength of 0.1315 nm were used to produce a diffraction pattern for copper. The first order diffraction (n = 1) occurred at an angle θ = 25.25°. Determine the spacing between the diffracting planes in copper.

Solution: The distance between the planes is found by solving the Bragg equation,

nλ = 2d sin θ,

ford.

This gives:   d=nλ2sinθ

=1(0.1315nm)2sin(25.25∘)=0.154nm

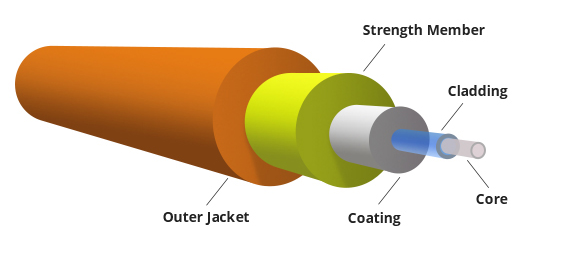
Q21) Discuss principle, construction and working of Optical Fibre?

Solution: A cable which is used to transmit the data through fibres (threads) or plastic (glass) is known as optical fibre cable. This cable includes a pack of glass threads which transmits modulated messages over light waves.

Principle: Optical Fibre works on the principle of Total Internal Reflection.

Total internal reflection:- When the light ray travels from denser medium to rarer medium the refracted ray bends away from the normal. When the angle of incidence is greater than the critical angle, the refracted ray again reflects into the same medium. This phenomenon is called total internal reflection. The refracted ray bends towards the normal as the ray travels from rarer medium to denser medium. The refracted ray bends away from the normal as it travels from denser medium to rarer medium.

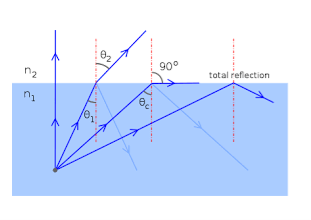
Figure – Total Internal Reflection

Characteristics of Optical Fibre

Figure: Optical Fibre

Construction of Optical Fibre:

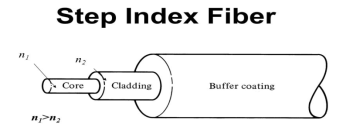
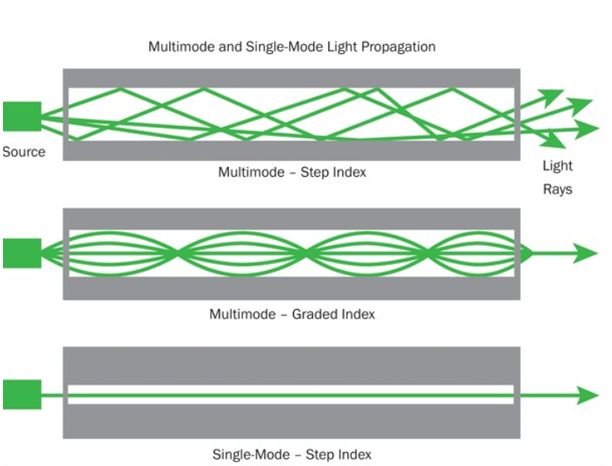
It consists of a very thin fibre of silica or glass or plastic of a high refractive index called the core. The core has a diameter of 10 um to 100 um. The core is enclosed by a cover of glass or plastic called cladding. The refractive index of the cladding is less than that of the core (which is a must condition for the working of the optical fibre). The difference between the two indicates is very small of order 10-3. The core and the cladding are enclosed in an outer protective jacket made of plastic to provide strength to the optical fibre. The refractive index can change from core to cladding abruptly (as in step-index fibre) or gradually (as in graded-index fibre).

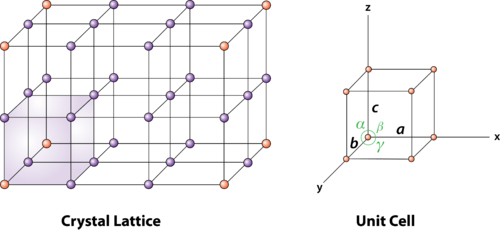
Figure Representation of Optical Fibre

Working of Optical Fibre

When a ray of light is incident on the core of the optical fibre at a small angle, it suffers refraction and strikes the core-cladding interface, As the diameter of the fibre is very small hence the angle of incidence is greater than the critical angle. Therefore, the ray suffers total internal reflection at the core-cladding interface and strikes the opposite interface. At this interface also, the angle of incidence is greater than the critical angle, so it again suffers total internal reflection. Thus, the ray of light reaches the other end of the fibre after suffering repeated total internal reflections along the length of the fibre. At the other end, the ray suffers refraction and emerges out the optical fibre.

We can see that the light travels in the core in a guided manner. Hence the communication through the optical fibre is sometimes referred as an optical waveguide.

Q22) Explain the terms acceptance angle, numerical aperture.

or

Derive expressions for the numerical aperture and fraction change in refractive index change of an optical fibre.

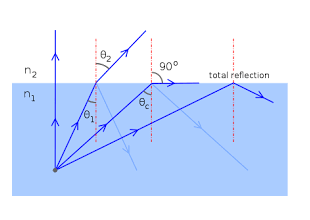
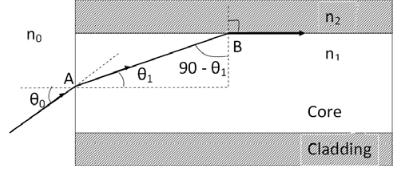
Solution: Acceptance angle

Definition:-Acceptance angle is defined as the maximum angle of incidence at the interface of air medium and core medium for which the light ray enters into the core and travels along the interface of core and cladding.

Let n0 be the refractive indices of air

n1 be the refractive indices of core

n2 be the refractive indices of cladding

Let a light ray OA is incident on the interface of air medium and core medium with an angle of incidence θ0

The light ray refracts into the core medium with an angle of refraction θ1 and the refracted ray AB is again incidenting on the interface of core and cladding with an angle of incident (90-θ1)

If (90-θ1) is equal to the critical angle of core and cladding media then the ray travels along the interface of core and cladding along the path BC. If the angle of incident at the interface of air and coreθ1<θ0 then (90-θ1) will be greater than the critical angle. Therefore,

The total internal reflection takes place.

According to Snell’s law at point A

n0Sin θ0 = n1 Sin θ1

Sin θ0= (n1 / n0) Sin θ1  ………(1)

According to Snell’s law at point B

n1Sin(90- θ1) = n2 Sin90  ………(2)

n1 Cosθ1 = n2   as(Sin90=1)

Cosθ1 = n2 /n1

Sinθ1 = (1-Cos2θ1)1/2

Sinθ1= (1- (n2 /n1)2)1/2

Sinθ1= ( n12- n22 )1/2/ n1  ………(3)

We know   Sin θ0= (n1 / n0) Sin θ1 from equation (1)

Substitute the value of  Sinθ1 from equation (3)

Sinθ0= (n1 / n0) *( n12- n22 )1/2/ n1

On simplification

Sinθ0= ( n12- n22 )1/2/ n0

θ0=Sin-1( n12- n22 )1/2/ n0  

 Acceptance Angle is θ0=Sin-1( n12- n22 )1/2/ n0  ………(4)

Numerical aperture

Definition: -Numerical aperture is defined as the light gathering capacity of an optical fibre and it is directly proportional to the acceptance angle. Numerically it is equal to the sin of the acceptance angle.

NA = Sin(acceptance angle)

NA = Sin {Sin-1 (( n12- n22 )1/2/ n0)}  from equation (4)

NA = (( n12- n22 )1/2/ n0)   ………(5)

If the refractive index of the air medium is unity i.e. n0=1 put in (5)

NA = ( n12- n22 )1/2    ………(6)

Fractionalchange in refractive index

∆= (n1- n2)/ n1

n1∆ = (n1- n2)     ………(7)

from equation (6), we have

NA = {( n1- n2 )( n1+n2 )}1/2

NA = { n1∆ (n1+n2 )}1/2   as n1∆ = (n1- n2) by Eq(7)

NA = { n1∆ 2n1}1/2    n1≈ n2,   so n1+n2 =2n1

NA = n1{2∆}1/2 

This gives the relation between Numerical aperture and Fractionalchange in refractive index.

Q23) What are the advantages and disadvantages of an optical fibre?

Solution: Advantages of fibre optic communication

The optical fibre communication has more advantages than convectional communication.

1. Enormous Bandwidth

2. Low Transmission Loss

3. Electric Isolation

4. Signal Security

5. Small Size and Less Weight

6. Immunity Cross Talk

1. Enormous bandwidth:- The information carrying capacity of a transmission system is directly proportional to the frequency of the transmitted signals. In the coaxial cable transmission the bandwidth range is up to around 500MHz only. Where as in optical fibre communication, the bandwidth range is large as 105 GHZ.

2. Low transmission loss:- The transmission loss is very low in optical fibres (i.e.KmdB/2.0) than compare with the conventional communication system. Hence for long distance communication fibres are preferred.

3. Electric isolation:- Since fibre optic materials are insulators, they do not exhibit earth and interface problems. Hence communicate through fibre even in electrically danger environment.

4. Signal security:- The transmitted signal through the fibre does not radiate, unlike the copper cables, a transmitted signal cannot be drawn from fibre without tampering it. Thus the optical fibre communication provides 100% signal security.

5. Small size and less weight:- The size of the fibre ranges from 10μm to 50μm, which is very small. The space occupied by the fibre cable is negligibly small compared to conventional electrical cables. Optical fibres are light in weight.

6. Immunity cross talk:- Since the optical fibres are dielectric wave guides, they are free from any electromagnetic interference and radio frequency interference. Since optical interference among different fibres is not possible, cross talk is negligible even many fibres are cabled together.

Disadvantages of Optical Fibre

The disadvantages of optical fibre include the following

Q24) Write a note on the applications of an optical fibre?

Solution: Application of optical fibre

Q25) Explain how the optical fibres are classified?

Solution: TYPES OF OPTICAL FIBRES

The types of optical fibres depend on the refractive index, materials used, and mode of propagation of light.

Example: 

Core: polymethylmethacrylate : Cladding: Co- Polymer

Core: Polystyrene  : Cladding: Methyl methacrylate

Example: 

Core: SiO2 Cladding: SiO2

Core: GeO2- SiO2 Cladding: SiO2

Mode of propagation:

Light propagates as electromagnetic waves through an optical fibre. All waves, having ray directions above the critical angle will be trapped within the fibre due to total internal reflection. However, all such waves do not propagate through the fibre. Only certain ray directions are allowed to propagate. The allowed directions correspond to the modes of the fibre. In simple terms, modes can be visualized as the possible number of paths of light in an optical fibre.

These fibres are used for long-distance transmission of signals. In general, the single mode fibres are step – index fibres. These types of fibres are made from doped silica. It has a very small core diameter so that it can allow only one mode of propagation and hence called single mode fibres.

The cladding diameter must be very large compared to the core diameter. Thus in the case of single mode fibre, the optical loss is very much reduced. The structure of a single mode fibre is given below.

Structure:

Core diameter         :         5-10μm

Cladding diameter            :      Generally around 125μm

Protective layer    :      250 to 1000μm

Numerical aperture         :         0.08 to 0.10

Band width    :         More than 50MHz km.

Application:

Because of high bandwidth, they are used in long haul communication systems.

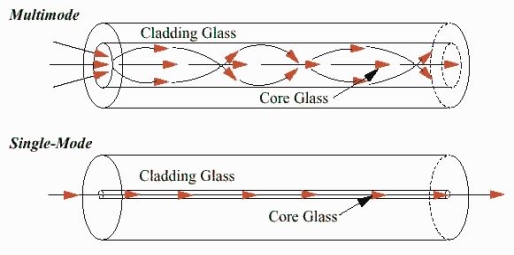
 These fibres are used for short-distance transmission of signals. The multi-mode fibres are useful in manufacturing both for step – index and graded index fibres. The multi-mode fibres are made by multi-component glass compounds such as Glass – Clad Glass, Silica – Clad – Silica, doped silica etc. Here the core diameter is very large compared to single mode fibres, so that it can allow many modes to propagate through it and hence called as Multi mode fibres. The cladding diameter is also larger than the diameter of the single mode fibres. The structure of the multimode fibre is as shown in the figure above.

Structure:

Core diameter  :         50-350μm

Cladding diameter           :         125μm - 500μm

Protective layer      :         250 to 1100μm

Numerical aperture         :         0.12 to 0.5

Band width    :         Less than 50MHz km.

 The total number of modes possible for such an electromagnetic wave guide is

Application:

Because of its less band width it is very useful in short haul communication systems.

It consists of a core surrounded by the cladding, which has a single uniform index of refraction. Step index-single mode fibres: A single mode step index fibre consists of a very thin core of uniform refractive index surrounded by a cladding of refractive index lower than that of core. The refractive index abruptly changes at the core cladding boundary. Light travels along a side path, i.e., along the axis only. So zero order modes is supported by Single Mode Fibre.

A multimode step index fibre consists of a core of uniform refractive index surrounded by cladding of refractive index lower than that of the core. The refractive index abruptly changes at the core cladding boundary. The core is of large diameter. Light follows zigzag paths inside the fibre. Many such zigzag paths of propagation are permitted in Multi-Mode Fibre. The Numerical Aperture of a Multi-mode fibre is larger as the core diameter of the fibre is larger

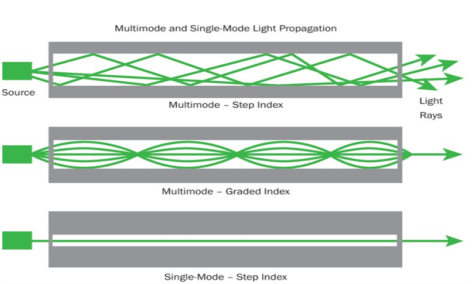
The refractive index of the optical fibre decreases as the radial distance from the fibre axis increases. GRIN fibre is one in which refractive index varies radially, decreasing continuously in a parabolic manner from the maximum value of n1, at the center of the core to a constant value of n2 at the core cladding interface.

In graded index fibre, light rays travel at different speeds in different parts of the fibre because the refractive index varies throughout the fibre. Near the outer edge, the refractive index is lower. As a result, rays near the outer edge travel faster than the rays at the center of the core. Because of this, rays arrive at the end of the fibre at approximately the same time. In effect light rays arrive at the end of the fibre are continuously refocused as they travel down the fibre. All rays take the same amount of time in traversing the fibre. This leads to small pulse dispersion.

 For a parabolic index fibre, the pulse dispersion is reduced by a factor of about 200 in comparison to step index fibre. It is because of this reason that first and second generation optical communication systems used near parabolic index fibres.

Q26) What do you meant by V-Number?
Solution: An optical fibre is characterized by one more important parameter, known as V-number which is more generally called normalized frequency of the fibre. It is given by the relation

V – number determines how many modes a fiber can support,  It is given by,

V = 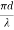NA

Where d is the diameter of the core,

l is the wavelength of light used

NA is the numerical aperture of the fibre.

V =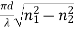

Or 

V =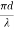      

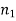
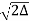
If V ≤ 2.405, then the fibre is single mode fibre (SMF)

 If V > 2.405, then the fibre is multimode fibre (MMF)

Q27)Consider a multimode step index fibre with n1 = 1.53 and n2 = 1.50 and λ= 1μm. If the core radius = 50 μm then calculate the normalized frequency of the fibre (V) and the number of guided mode.

Solution: d = 2r = 2 x 50 x 10-6 m

V = 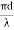NA  = =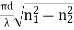

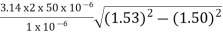
=94.72= normalized frequency

Total number of guided mode = M = V2/2 = 4486.

Q28) Discuss Semiconductor Laser?

Solution: Semiconductor Laser

It is a solid state semiconductor laser. It is specifically fabricated p-n junction diode. This diode emits laser light when it is forward biased. A semiconductor laser is a device that causes laser oscillation by flowing an electric current to semiconductor. The mechanism of light emission is the same as a light-emitting diode (LED). Light is generated by flowing the forward current to a p-n junction. In forward bias operation, the p-type layer is connected with the positive terminal and the n-type layer is connected with the negative terminal, electrons enter from the n-type layer and holes from the p-type layer. When the two meet at the junction, an electron drops into a hole and light is emitted at the time.

Semiconductor lasers represent one of the most important class of lasers in use today, not only because of the large variety of direct applications in which they are involved but also because they have found a widespread use as pumps for solid state lasers.

Semiconductor lasers require, for the active medium, a direct gap material and accordingly, the normal elemental semiconductors like Si or Ge cannot be used. The majority of semiconductor-laser materials are based on a combination of elements belonging to the third group of the periodic table such as Al, Ga, In with elements of the fifth group such as N, P,As, Sb. Examples include the best known GaAs as well as some ternary AlGaAs, InGaAs and quaternary  In GaAsP alloys.

InGaN semiconductor lasers the best candidates for semiconductor laser emission in the very important blue-green spectral region. Semiconductor laser materials are not limited to III–V compounds, however. For the blue-green end of the spectrum we note that there are wide-gap semiconductors using a combination between elements of the second group (such as Cd and Zn) and of the sixth group (S, Se).

PRINCIPLE

When a p-n junction diode is forward biased, the electrons from n – region and the holes from the p- region cross the junction and recombine with each other.

 During the recombination process, the light radiation (photons) is released from a certain specified direct band gap semiconductors like Ga-As. This light radiation is known as recombination radiation.

The photon emitted during recombination stimulates other electrons and holes to recombine. As a result, stimulated emission takes place which produces laser.

Figure: 11

CONSTRUCTION

The basic structure of a semiconductor laser is shown in Figure.The active medium is a p-n junction diode made from the single crystal of gallium arsenide.  The active layer called as light emission layer sandwiched between the p- and n-type clad layers i.e. double hetero structure is formed on an n-type substrate and voltage is applied across the p-n junction from the electrodes. This crystal is cut in the form of a platter having thickness of 0.5μmm. Both edges of the active layer has mirror-like surface. When forward voltage is applied, electrons combine with holes at the p-n junction, and emit the light.

This light is not a laser yet; it is confined within the active layer because the refractive index of the clad layers is lower than that of the active layer. In addition both ends of the active layer act as a reflecting mirror where the light reciprocates in the active layer. Then, the light is amplified by the stimulated emission process and laser oscillation is generated.

The photon emission is stimulated in a very thin layer of PN junction (in order of few microns). The electrical voltage is applied to the crystal through the electrode fixed on the upper surface. The end faces of the junction diode are well polished and parallel to each other. They act as an optical resonator through which the emitted light comes out.

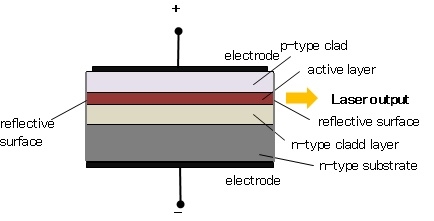
Figure: 12

WORKING

When the PN junction is forward biased with large applied voltage, the electrons and holes are injected into junction region in considerable concentration

The region around the junction contains a large amount of electrons in the conduction band and a large amount of holes in the valence band.

If the population density is high, a condition of population inversion is achieved. The electrons and holes recombine with each other and this recombination’s produce radiation in the form of light.

 When the forward – biased voltage is increased, more and more light photons are emitted and the light production instantly becomes stronger. These photons will trigger a chain of stimulated recombination resulting in the release of photons in phase.

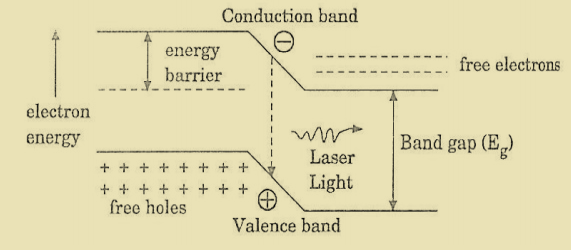
Figure: 13

The photons moving at the plane of the junction travels back and forth by reflection between two sides placed parallel and opposite to each other and grow in strength.

After gaining enough strength, it gives out the laser beam of wavelength 8400Å. The nature of output is continuous wave or pulsed output. The power output from this laser is 1mW. The wavelength of laser light is given by

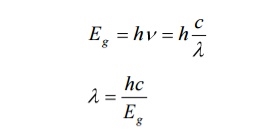
Where Eg is the band gap energy in joule.

ADVANTAGES

DISADVANTAGES 

 APPLICATION

Q29) Discuss Bose-Einstein Distribution Law?

Solution: The basic postulates of BE statistics are:-

(i)The associated particles are identical and indistinguishable.

(ii)Each energy state can contain any number of particles.

(iii)Total energy and total number of particles of the entire system is constant

(iv)The particles have zero or integral spin,i.e. 0ℏ, 1 ℏ,5 ℏ,50 ℏetc, where ℏ is the unit of spin.

(v) The wavefunction of the system is symmetric under the positional exchange of any two particles. Examples: photon, phonon, all mesons (,,) etc., these are known as Bosons.

Symmetric and Anti-symmetric wave function

Suppose the allowed wave function for a n-particles system is ψ(1,2,3,.....,r,s,...n), where the integers within the argument of ψ represent the coordinates of the n-particles relative to some fixed origin. Now, if we interchange the positions of any two particles, say, r and s, the resulting wave function becomes ψ(1,2,3,....s,r,.....n). The wave function ψ is said to be symmetric when

ψ(1,2,3,.....,r,s,...n) = ψ(1,2,3,....s,r,.....n)

andAnti-symmetric when

ψ(1,2,3,.....,r,s,...n) = -ψ(1,2,3,....s,r,.....n)]

Bose-Einstein Distribution Law:

Let Ni number of identical, indistinguishable, non-interacting particles are to be distributed among gi quantum states each having energy Ei. So, in the ith energy level, there are (Ni+gi) total objects. Keeping the first quantum state fixed, the remaining (Ni+ gi-1)objects can permuted in (Ni+ gi-1)! possible ways. But since the particles and the quantum states are indistinguishable, we have to deduct Ni! ways and (gi–1)! ways from the all possible ways to get effective number of arrangements. Thus total number of possible ways of arrangement for theith state is

     ……….(1)

Hence the total number of ways of the entire distribution of N particles in n number of energy levels of the system is

     ……….(2)

wheredenotes the product symbol.If we assume that Niand gi are very large, equation (2) reduces to             

        ……….(3)

Taking natural logarithm of both the sides of equation (3) we get,

  ……….(4)

using Stirling approximation, Now, differentiating equation (4) to obtain the most probable distribution, we get,

Also we have other two conditions given by

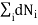 0     (conservation of total no of particles)………..(5)

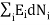 0    (conservation of total energy) ………..(6)

Multiplying equation (5) by (-α) and equation (6 )by (-β) and then adding with equation (4 )we get,

    ………..(7)

Since dNi’s are independent of one another, the above equation holds only if,

  ………..(8)

Now the Bose-Einstein distribution function is given by

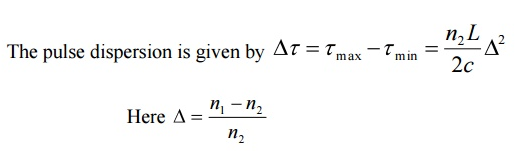       ………..(9)

which represents the probability of finding a boson with energy Ei.

Q30) Discuss FD statistics?

Solution:

The basic postulates of FD statistics are:-

(i)Particles are identical and indistinguishable.

(ii)Total energy and total number of particles of the entire system is constant (iii)Particles have half-integral spin, i.e.etc,, , .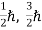

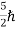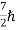(iv)Particles obey Pauli’s exclusion principle, i.e. no two particles in a single system can have the same value for each of the four quantum numbers. In other words, a single energy state can contain at best a single particle with appropriate spin.

(v) The wave function of the system is anti-symmetric under the positional exchange of any two particles.

Examples: electron, proton, neutron, all hyperons (Λ,Σ,Ξ,Ω) etc., these are known as Fermions.

Fermi-Dirac Distribution Law:

Consider a system of N indistinguishable, non-interacting particles obeying Pauli’s exclusion principle. Let N1, N2, N3, ....Ni,....Nn Particles in the system have energies E1, E2, E3, ....,Ei,...En respectively and let gi is the number of degenerate quantum states in the energy level Ei. According to Pauli’s exclusion principle a single quantum state can be occupied by at best one particle. Since Ni particles are to be distributed among gi degenerate states (gi ≥Ni) having the same energy Ei, N states will be filled up and (gi -Ni) states will remain vacant. Now gi states can be arranged in gi! possible ways. But since the particles and the quantum states are indistinguishable, we have to deduct Ni! ways and (gi -Ni)! ways from the all possible ways to get effective number of arrangements. Thus total number of possible ways of arrangement for the ith state is

      …………(1)

Hence the total number of ways for the entire distribution of N particles in n number of energy levels of the system is

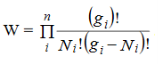      …………(2)

wheredenotes the product symbol.Now taking natural logarithm on both sides of equation (2) and applying Stirling approximation, we get,

   …………(3)

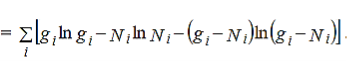  …………(4)

Now, differentiating equation (4) to obtain the most probable distribution, we get,

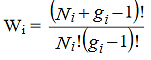  …………(5)

Considering the conservation of total energy and total number of particles, we can write

Also we have other two conditions given by

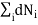 0     (conservation of total no of particles)………..(6)

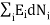 0    (conservation of total energy) ………..(7)

Multiplying equation (6) by (-α) and equation (7)by (-β) and then adding with equation (5)we get,

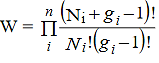    ………..(8)

Since dNi’s are independent of one another, the expression in thebracket of equation (8)is zero for each Ni. Thus

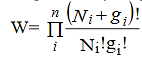       ………..(9)

Hence the Fermi-Dirac distribution function is given by

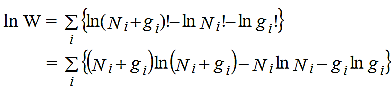      ………..(10)

which represents the probability of finding a fermion with energy Ei.