Unit - 3

Function and Recursion

Q.1) Write the advantages of functions ?

Ans : Advantages of function

The following are some of the benefits of using C functions.

●      We may prevent rewriting the same logic/code in a program by using functions.

●      C functions can be called any number of times and from any location in a program.

●      When a large C program is divided into multiple functions, we can easily monitor it.

●      The greatest accomplishment of C functions is reusability.

●      In a C program, however, function calling is always an overhead.

Q.2) Describe Quick sort ?

Ans : Quick sort

Quick sort is the most efficient method of sorting .It uses divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.

Algorithm to implement Quick Sort is as follows.

Consider array A of size n to be sorted. p is a pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.

C function for Quick sort

x = 0,  y = n-1

void Quicksort(A,x,y)

{

if(x<y)

{

first=x;

last=y;

while(first<last)

{

while(A[first]<p)

first++;

while(A[last]>p)

last--;

if(first<last)

swap(A[first],A[last]);

}

swap(A[x],A[y])

Quicksort(A,x,last-1);

Quicksort(A,first+1,y);

}

Q.3) Write any example of merge sort ?

Ans : Example of merge sort

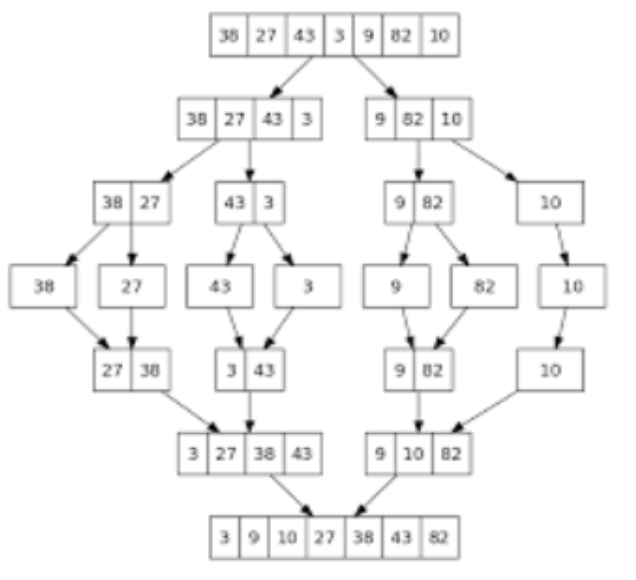
Apply merge sort for the following list of elements: 38, 27, 43, 3, 9, 82, 10

Analysis of merge sort:

Q.4) What are the pros and cons of merge sort ?

Ans : Pros

●      The number of comparisons carried out is almost ideal.

●      Mergesort is never going to degrade to O (n2)

●      It is applicable to files of any size.

Cons

●      Using extra memory O(n).

Q.5) Write any example of quick sort ?

Ans : Example of Quick sort

Apply Quicksort on array

 A= {27,6,39,2,65,12,57,18,49,19}

Here again first<last so we swap A[first] and A[last]. Swapping 65 and 18 we get

Repeat steps 2,3 and 4.

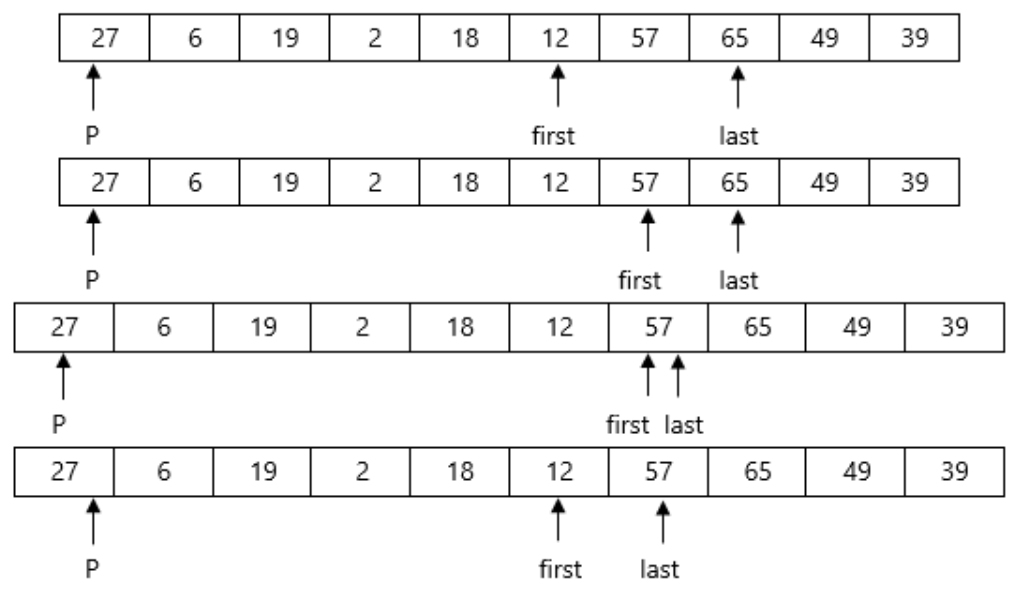
Now First>last so we swap pivot p with A[last]. Swapping 27 and 12 we get

Here we complete Pass 1.Now pivot element is 27 and it divides the array in left and right partitions. We can see that elements less than pivot are in the left partition and elements greater than pivot are in the right partition.

Now we continue the same procedure for the left and right partition.  Here we see results of corresponding passes.

Pass 2 :

Pass 3 :

Pass 4 :

Pass 5 :

Pass 6 :

Pass 7 :

Q.6) Write an example for factorial ?

Ans : The factorial of a positive number is the product of the integral values from 1 to the number itself.

Eg. 5!=5*4*3*2*1

  120

Recursive Factorial:

 The factorial algorithm can be defined recursively as follows

Factorial(n) =    1      if n=0

   n*(Factorial(n-1))   if n>0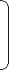 

Algorithm:

Calculate factorial of n

   fact(n) 

return 1

2.  else

return(n*fact(n-1))

3.  endif

end fact(n)

Fig 1: recursion of factorial number

Program to find factorial of a number using recursion.

#include<stdio.h>

#include<conio.h>

int rec (int x);

void main()

{

int a, fact;

printf("\nEnter any number: ");

scanf ("%d", &a);

fact=rec(a);

printf("\nFactorial Value = %d", fact);

getch();

}

int rec (int x)

{

int f;

if (x==1)

return (1);

else

f=x*rec(x-1);

return (f);

}

Q.7) Define merge sort ?

Ans : Merge sort

Merge sort consists of two phases as divide and merge.

●  In the divide phase, each time it divides the given unsorted list into two sublists until each sub list gets a single element then sorts the elements.

●  In the merge phase, it merges all the solutions of sub lists and finds the original sorted list.

Features :

●   Is an algorithm dependent on comparison?

●   A stable algorithm is

●   A fine example of the strategy of divide & conquer algorithm design

●   John Von Neumann invented it.

Steps to solve the problem:

Step 1: if the length of the given array is 0 or 1 then it is already sorted, else follow  step 2.

Step 2: split the given unsorted list into two half parts

Step 3: again divide the sub list into two parts until each sub list get single element

Step 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.

Step 5: merge the elements same as divide phase to get the sorted list

Algorithm:

Q.8) Write a program for fibonacci series ?

Ans : Fibonacci series

The first two numbers of the Fibonacci series are 0,1. The next number is the sum of the previous two numbers.

  Eg.   0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

●      1 is calculated by adding previous two numbers(0+1)

●      2 is calculated by adding the two numbers before it (1+1)

●      Similarly, the 3 is found by adding the two numbers before it (1+2), and so on

Algorithm:

 int fib(int n)

 {

  return n;

2.  else

  return (fib(n-1) + fib(n-2));

 }

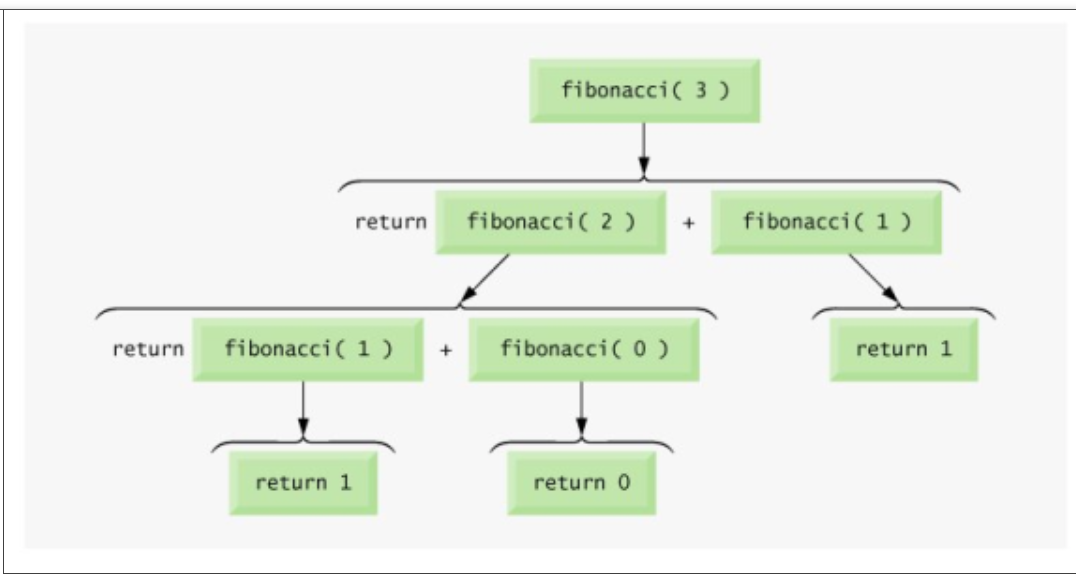
Fig 2: fibonacci series

Program to print Fibonacci series using recursion.

#include<stdio.h>

#include<conio.h>

int Fibonacci(int);

void main()

{

   int n, i, c=0;// n is no. of terms in Fibonacci series.

   printf(“Enter no. of terms in Fibonacci series”);

   scanf("%d",&n);

   printf("Fibonacci series\n");

   for( i= 1 ; i <= n ; i++ )

   {

   printf("%d\n", Fibonacci(c));

   c++;

   }

   getch();

}

int Fibonacci(int x)

{

   if ( x == 0 )

   return 0;

   else if ( x == 1 )

   return 1;

   else

   return ( Fibonacci(x-1) + Fibonacci(x-2) );

}

Q.9) Write a program for the Ackermann function using recursion ?

Ans : Ackermann function

The Ackermann function is the most basic example of a well-defined total function that is computable but not primitive recursive, serving as a counterexample to the early 1900s assumption that any computable function was also primitive recursive. It grows at a faster rate than an exponential or multiple exponential function.

The source code for a C program to implement the Ackermann function using recursion is shown below, which has been successfully compiled and run on a Windows system to generate the desired output:

Program  to implement Ackermann function using Recursion:

/* C Program to implement Ackermann function using recursion */

#include<stdio.h>

int A(int m, int n);

main()

{

        int m,n;

        printf("Enter two numbers :: \n");

        scanf("%d%d",&m,&n);

        printf("\nOUTPUT :: %d\n",A(m,n));

}

int A(int m, int n)

{

        if(m==0)

                return n+1;

        else if(n==0)

                return A(m-1,1);

        else

                return A(m-1,A(m,n-1));

}

Output :

Enter two numbers ::

1

0

OUTPUT :: 2

Q.10) Explain about function ?

Ans : Library Function

A function which is predefined in c language is called a library function. Library function is also called a built-in function of C language. The definition of the library function is stored in the respective header file. Library functions are used to perform dedicated operations like taking input from the user, displaying output, string handling operation, etc. Library functions are readily available and programmers can directly use it without writing any extra code. For example, printf () and scanf () are library functions and their definition is stored in the stdio header file.

User Defined Functions

User defined function is the block of code written by a programmer to perform a particular task. The compiler doesn’t have any idea about the user defined function so the programmer has to define and declare these functions inside the program body. Programmers can define these functions outside the main function but declaration of user defined function should be present in main function only. Whenever the compiler executes function call (function declaration) then the compiler shifts the flow of program execution to the definition part of the user defined function.

Example

#include<stdio.h>

#include<conio.h>

int add(int x, int y)

{

int sum;

sum = x + y;

return (sum);

}

main()

{

int a,b,c;

a = 15;

b = 25;

c = add (a,b);

printf(“\n Addition is %d”, c);

}

Output:

Addition is 40

Q.11) What do you mean by Parameter passing by value ?

Ans : Parameter passing by value

This is the default way of passing the parameters to the function. This is achieved by passing the copy of data to the function. This mechanism is also called as call by value. In case of parameter passing by value, the changes made to the formal arguments in the called function have no effect on the values of actual arguments in the calling function.

This mechanism is used when programmers don't want to change the value of passed parameters. When parameters are passed by value then functions in C create copies of the passed in variables and do required processing on these copied variables.

Pass-by-value is implemented by actual data transfer so additional storage is required to maintain the copies of passed parameters.

Example:

#include<stdio.h>

#include<conio.h>

/* function declaration goes here */

void swap(int p1, int p2);

int main()

{

 int a =10;

 int b =20;

 printf(“Before: value of a = %d and value of b = %d\n”, a,b);

 swap(a,b);

 printf(“After : value of a = %d and value of b = %d\n”, a,b);

 getch();

}

void swap(int p1, int p2)

{

 int t;

 t = p2;

 p2 = p1;

 p1 = t;

 printf(“Value of a (p1) = %d and value of b(p2) = %d\n”, p1,p2);

}

Output :

Before: Value of a = 10 and value of b = 20

Value of a (p1) = 20 and value of b (p2) = 10

After: Value of a = 10 and value of b = 20

Note: In the above example the values of “a” and “b” remain unchanged before calling swap function and after calling swap function.

Q.12) Explain parameters passing by references  with example ?

Ans : Parameters passing by references

This mechanism is used when programmers want a function to do the changes in passed parameters and reflect those changes back to the calling function. This mechanism is also called a call by reference. This is achieved by passing the address of the variable to the function and function body can directly work over the addresses. Advantage of pass by reference is efficiency in both time and space. Whereas disadvantages are access to formal parameters is slow and inadvertent and erroneous changes may be made to the actual parameter.

Example:

#include<stdio.h>

#include<conio.h>

void swap(int *p1, int *p2);

int main()

{

 int a =10;

 int b =20;

 printf(“Before: value of a = %d and value of b = %d\n”, a,b);

 swap(&a, &b);

 printf(“After : value of a = %d and value of b = %d\n”, a,b);

 getch();

}

void swap(int *p1, int *p2)

{

 int t;

 t = *p2;

 *p2 = *p1;

 *p1 = t;

 printf(“Value of a (p1) = %d and value of b(p2) = %d\n”, *p1, *p2);

}

Output :

Before: Value of a = 10 and value of b = 20

Value of a (p1) = 20 and value of b(p2) = 10

After: Value of a = 20 and value of b = 10

Note: In the above example the values of “a” and “b” are changed after calling the swap function.

Q.13) What is the difference between call by value and call by reference ?

Ans : Difference between call by value and call by references