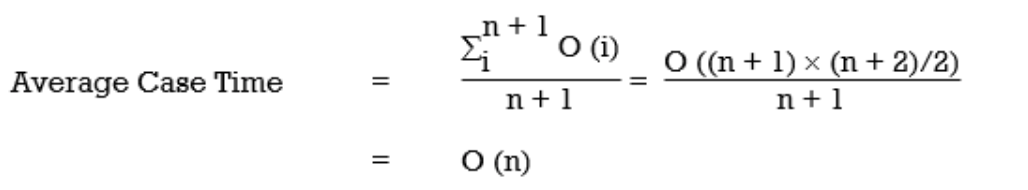Unit - 5
Basic Algorithms
Q.1) Explain linear search with an example ?
Ans : Linear search
Given a collection of objects, the goal of search is to find a particular object in this collection. The objects have key values on which search is performed and data values which correspond to the information one wishes to retrieve once an object is found.
For example, a telephone book is a collection of names on which one searches and telephone numbers which correspond to the data being sought. The collection of objects is often stored in a list or an array. Given a collection of objects in an array A[1.. n], the ith element A[i] corresponds to the key value of the ith object in the collection. The input to a search algorithm is an array of objects A, the number of objects n, and the key value being sought x.
Thus Algorithm for Linear Search is
Function for Linear search is
find(values, target)
{
for(i =0; i<values.length; i++)
{
if(values[i] ==target)
return i;
}
return-1;
}
If an element is found this function returns the index of that element otherwise it returns –1.
Example of linear search
we have an array of integers, like the following:
Elements → | 9 | 6 | 7 | 12 | 1 | 5 |
Index→ | 0 | 1 | 2 | 3 | 4 | 5 |
Let’s search for the number 7. According to the function, the linear search index for element 7 should be returned. We start at the beginning and check the first element in the array.
9 | 6 | 7 | 12 | 1 | 5 |
First element is 9.Match is not found and hence we move to the next element i.e 6.
9 | 6 | 7 | 12 | 1 | 5 |
Again match is not found so move to next element i.e.7.
9 | 6 | 7 | 12 | 1 | 5 |
0 | 1 | 2 | 3 | 4 | 5 |
We found the match at index position 2. Hence output is 2.
If we try to find element 10 in the above array, it will return –1,as 10 is not present in the array.
Q.2) Write an algorithm for recursive binary search ?
Ans : Algorithm for recursive binary search
intBinarySearch(int A[], int x, int Low, int High)
{
if(High>Low)
return-1;
int mid = (High + Low) / 2;
if(A[mid] == x)
return mid;
if(A[mid] < x)
returnBinarySearch(A, x, mid+1, High);
}
Q.3) Write a program of linear search ?
Ans : #include<stdio.h>
#include<conio.h>
int search(int [], int, int);
void main()
{
int a[20], k, i, n, m;
clrscr();
printf(“\n\n Enter the array elements \n\n”);
for(i =0; i<n; i++)
{
scanf(“%d”, &a[i]);
}
printf(“\n\n Enter the element for search \n”);
scanf(“%d”, &k);
m = search(a,n,k);
if(m== -1)
{
printf(“\n Element is not found in list”);
}
else
{
printf(“\n\n Element is found at location %d”, m);
}
getch();
}
int search(int a[], int n, int k)
{
int i;
for(int i =0; i<n; i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return -1;
}
}
Q.4) Explain binary search with an example ?
Ans : Binary Search
Binary Search requires a sorted array.
Steps to perform binary search on sorted array A of size n are as follows.
Mid=(Low + High)/2
3. Compare the input key value with the key value of the middle element of the array. It has 3 possibilities.
Case 1 : If keys match then return mid and print element found.
if(key == A[mid])
return mid
Case 2 : If the key is less than the middle element then the element is present in the left half of the array. Update High and goto step 2.
if(key<A[mid])
High = mid -1
Goto step 2
Case 3 : If the key is greater than the middle element then the element is present in the right half of the array. Update Low and goto step 2.
if(key>A[mid])
Low = mid+1
goto step2
Case 4 : if(Low>High)
Print element not found.
Iterative algorithm for Binary Search
intBinarySearch(int a[], int x)
{
int mid, n;
int Low = 0;
int High = n-1;
while (Low ≤ High)
{
mid = (Low + High) / 2;
if(a[mid] == x)
return mid;
if(A[mid] > x)
High = mid -1;
else Low = mid + 1;
}
return -1;
}
Example : Let array A= {–1, 5, 6, 18, 19, 25, 46, 78, 102, 114}. We want to find element ‘6’ using binary search.
–1 | 5 | 6 | 18 | 19 | 25 | 46 | 78 | 102 | 114 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Solution:
Step 1 : Low=0, High= 9
Step 2 :Mid=(Low + High)/2
Mid = (0+9)/2 =4.5 i.e 4. It means the middle element is located at position 4. So A[Mid] is 19.Thus
Low=0
Mid=4
High=9
Low |
|
|
| Mid |
|
|
|
| High |
–1 | 5 | 6 | 18 | 19 | 25 | 46 | 78 | 102 | 114 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Step 3 :Compare 6 with 19. It satisfies case 2 of step 3. so High= 4–1=3 and the element is present in the left half of the array. We can ignore the right half of the array.
Repeat step 2. So mid= (0+3)/2 = 1.5 i.e 1. mid is at position 1. Element 5 is present at position 1.
Low = 0
Mid = 1
High = 3
Low | Mid |
| High |
|
–1 | 5 | 6 | 18 | 19 |
0 | 1 | 2 | 3 | 4 |
Again compare 5 with 6. It satisfies case 3 of step 3. so
Low = 1+1=2.
Repeat step 2. Mid= (2+ 3)/2= 2.5 i.e 2 .Mid is at position 2. Element 6 is at position 2.
Low=2
Mid=2
High=3
|
|
|
|
|
Low | Mid |
| High |
|
–1 | 5 | 6 | 18 | 19 |
0 | 1 | 2 | 3 | 4 |
Compare 6 with 6.
Match is found. Return the position and print element found.
Q.5) What is the complexity of linear search ?
Ans : Complexity of linear search
Let us assume element x is to be searched in array A of size n.
An algorithm can be analyzed using the following three cases.
1. Worst case
2. Average case
3. Best case
|
3. Best Case : In linear search , the best case occurs when x is present at the first location. So time complexity in the best case would be O(1).
Q.6) Write a program for binary search ?
Ans : Program for Binary search
#include<stdio.h>
#include<conio.h>
void main()
{
int n, i, search, f=0, low, high, mid, a[20];
clrscr();
printf(“Enter the number of elements :”);
scanf(“%d”, &n);
for(i=1; i≤n; i++)
{
printf(“Enter the number in ascending order a[%d]=”, i);
scanf(“%d”, &a[i]);
}
printf(“Enter the element to be searched:”);
scanf(“%d”, &search);
low = 0;
high = n-1;
while(low<=high)
{
mid = (low + high) / 2;
if(search<a[mid])
{
high = mid - 1;
}
else if(search>a[mid])
{
low = mid + 1;
}
else
{
f = 1;
printf(“Element is found at the position %d:”, mid);
exit();
}
}
if(f==0)
{
printf(“Element not found”);
}
getch();
}
Q.7) Write the merits and demerits of linear search ?
Ans : Merits of linear search :
● Simple and easy to implement
● It works well even on unsorted arrays.
● It is memory efficient as it does not require copying and partitioning of the array being searched.
Demerits :
● Suitable only for a small number of values.
● It is slow as compared to binary search.
Merits of binary search :
● Binary Search is fast and efficient.
● Suitable for a large number of values.
Demerits :
● Binary search works only on sorted arrays or lists.
Q.8) What is the complexity analysis of binary search ?
Ans : Complexity Analysis of Binary Search :
Assume our array size is 16.
When n= 16 BinarySearch is called to reduce size to n=8.
When n= 8 BinarySearch is called to reduce size to n=4.
When n= 4 BinarySearch is called to reduce size to n=2.
When n= 2 BinarySearch is called to reduce size to n=1 .
Thus we see that BinarySearch function is called 4 times
i.e. 4 elements of the array were examined for n =16.
Note that 16 = 24
Let us consider a more general case where n is still a power of 2. Let us say n =2k
After k searches, the while loop is executed k times and n reduces to size 1. Let us assume that each run of the while loop involves at most 4 operations.
Thus total number of operations: 4k.
The value of k can be determined from the expression
2k = n
Taking log of both sides
k = log n
Thus total number of operations = 4 log n.
We conclude that the time complexity of the Binary search method is O(log n), which is much more efficient than the Linear Search method.
Q.9) Explain bubble sort with example ?
Ans : Bubble sort
Steps to perform Bubble sort are as follows.
Assume we want to sort the elements in ascending order and no two elements are equal.
Let us consider array A of size n. Then Algorithm for Bubble sort is
1. Set i to 0.
2. Set j to 0.
3. if(A[j]>A[j+1])
swap A[j],A[j+1]
4. Increment j
5. if j<(n–1–i) goto step 3
6. Increment i
7. if(i<n–1) goto step 2.
Example : Suppose the following numbers are stored in an array A:
32 | 51 | 27 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
We apply bubble sort to array A. We discuss each pass separately.
Pass 1 :
32 | 51 | 27 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Array A becomes
32 | 27 | 51 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7
|
3. Compare j[2] and j[3]. Since 51 < 85, array is not altered.
4. Compare j[3] and j[4]. Since 85 > 66, interchange 85 and 66 as follows:
32 | 27 | 51 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Array A becomes
32 | 27 | 51 | 66 | 85 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
5. Compare j[4] and j[5]. Since 85 > 23, interchange 85 and 23 as follows:
32 | 27 | 51 | 66 | 85 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Array A becomes
32 | 27 | 51 | 66 | 23 | 85 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
6. Compare j[5] and j[6]. Since 85 > 13, interchange 85 and 13 as follows:
32 | 27 | 51 | 66 | 23 | 85 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
32 | 27 | 51 | 66 | 23 | 13 | 85 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
7. Compare j[6] and j[7]. Since 85 > 57, interchange 85 and 57 as follows:
32 | 27 | 51 | 66 | 23 | 13 | 85 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Array A becomes
32 | 27 | 51 | 66 | 23 | 13 | 57 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
At the end of this first pass, the largest number, 85, has moved to the last position. However, the rest of the numbers are not sorted, even though some of them have changed their positions.
Pass 2 will move the second last number to the second last position, Pass 3 will move the third last number to the third last position and so on. Here we show an array after every pass.
Pass 2 :
27 | 33 | 51 | 23 | 13 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 3 :
27 | 33 | 23 | 13 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 4:
27 | 23 | 13 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 5 :
23 | 13 | 27 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 6 :
13 | 23 | 27 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Hence the array is sorted in 6 passes.
Q.10) Write a program for bubble sort ?
Ans : Program for Bubble sort
#include<stdio.h>
#include<conio.h>
void bubble_sort(int A[], int n);
int main()
{
int A[100], n, i, j, swap;
printf(“Enter number of elements \n”);
scanf(“%d”, &n);
printf(“Enter the elements \n”);
for(i=0; i<=n; i++)
scanf(“%d”, &A[i]);
bubble_sort(A,n);
printf(“Sorted list in ascending order : \n”);
for(i=0; i<n; i++)
printf(“%d\n”, A[i]);
return 0;
}
void bubble_sort(int A[], int n)
{
int i, j, t;
for(j=0; j<(n-i-1); i++)
{
for(j=0; j<(n-i-1); j++)
{
if(A[j]>list[j+1])
{
/* SWAPPING */
t = A[j];
A[j] = A[j+1];
A[j+1] = t;
}
}
}
}
Complexity Bubble sort:
Suppose we have a list with n elements, and each element performs n – 1 comparisons with elements to its left, and swap, if necessary.
Best Case: If the list is already sorted, only one iteration is performed and complexity is O(1).
Average and Worst case: For n elements at most n – 1 swap operations are performed in each pass. The worst and average case complexity is O(n2).
Q.11) Explain insertion sort with example ?
Ans : Insertion sort
Insertion Sort reads all elements from 1 to n and inserts each element at its proper position. This sorting method works well on a small list of elements.
Procedure for each pass is as follows.
Pass 1 : A[l] by itself is trivially sorted.
Pass 2 : A[2] is inserted either before or after A[l] so that: A[l], A[2] is sorted.
Pass 3 : A[3] is inserted into its proper place so that: A[l], A[2], A[3] is sorted.
Pass 4 : A[4] is inserted into its proper place A[l], A[2], A[3], A[4] is sorted.
Pass N : A[N] is inserted into its proper place in so that:
A[l], A[ 2 ] , . . . , A[ N ] is sorted
Example :We will apply insertion sort on the original list of Fig.3.Assume we are arranging elements in ascending order.
25 | 79 | 41 | 9 | 34 | 60 |
Fig 1: Original List
C function for insertion sort
void insertionsort(int A[]; int n)
{
int i, p, temp, j;
for(i=1; i<=n; i++)
{
p = 0;
temp = A[i];
for(j=i-1; j≥0 && !p;)
if(temp < A[j])
{
A[j+1] = A[j];
j--;
}
else
p = 1;
A[j +1] = temp;
}
return;
}
Q.12) Write a program to implement insertion sort ?
Ans : Program of insertion sort
#include<stdio.h>
int main()
{
int n, A[100], i, j, t;
printf(“Enter number of elements \n”);
scanf(“%d”, &n);
printf(“Enter %d integers \n”, n);
for(i = 0; i<n; i++)
{
scanf(“%d”, &A[i]);
}
for(i=1; i<= (n-1); i++)
{
j = i;
while(j>0 && A[j] < A[j-1])
{
t = A[j];
A[j] = A[j-1];
A[j-1] = t;
j--;
}
}
printf(“Sorted list in ascending order: \n”);
for(i=0; i<=n-1; i++)
{
printf(“%d\n”, A[i]);
}
return 0;
}
Output :
Enter number of elements
5
Enter 5 integers
9
4
2
5
3
Sorted list in ascending order
2
3
4
5
9
Q.13) Explain selection sort with example ?
Ans : Selection sort
Assume we want to sort the list in ascending order. Selection sort finds the smallest element from an unsorted list and swap it with the element in first position. Then it finds the second smallest element and swaps it with the element at second position.
This process is repeated till the entire list is sorted in ascending order. Each time we swap elements, we say that we have completed a sort pass. A list of n elements requires n–1 passes to completely rearrange the data.
Procedure for every pass is as follows.
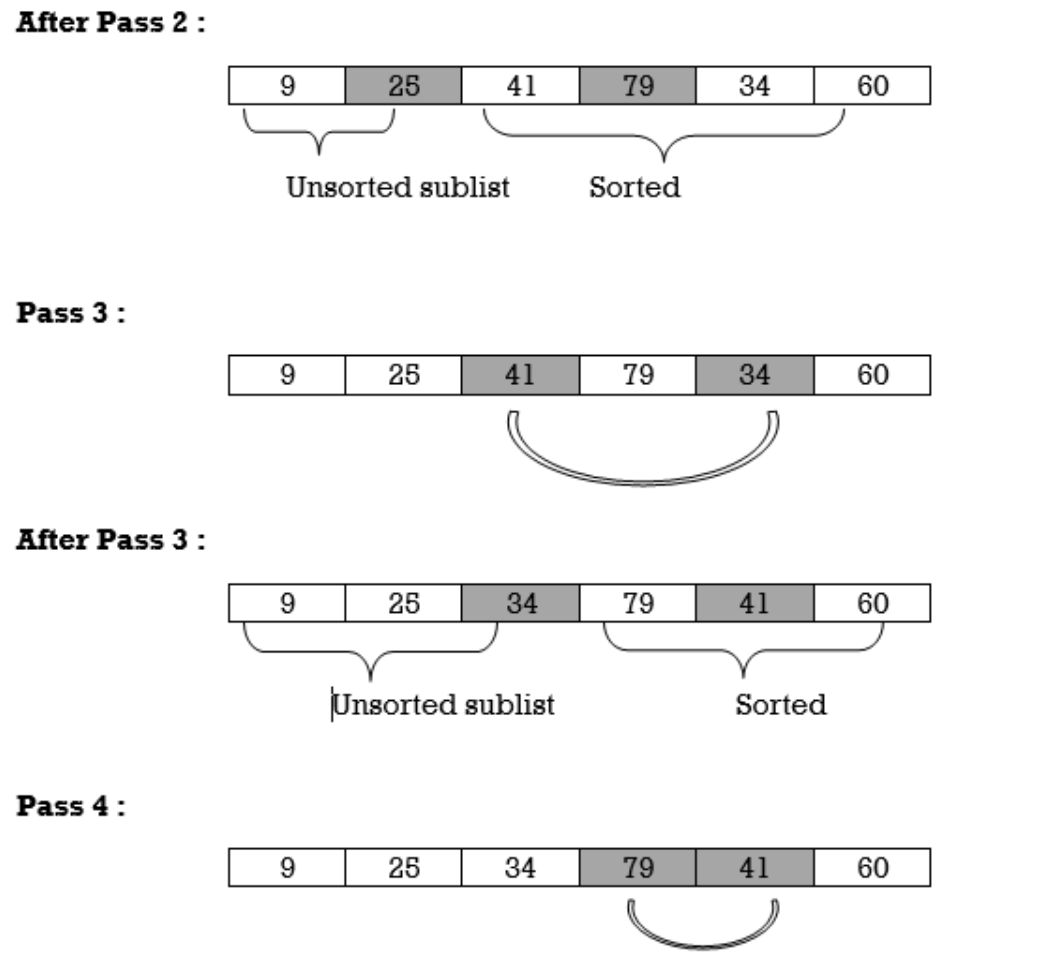
Pass 1 : Find the position P of the smallest in the list of N elements A[l], A[2], . . . , A[N], and then interchange A[P] and A[1] . Then A[1] is sorted.
Pass 2 : Find the position P of the smallest in the sublist of N –1 elements A[2], A[3],. . . , A[N], and then interchange A[P]and A[2]. Then A[l], A[2] is sorted.
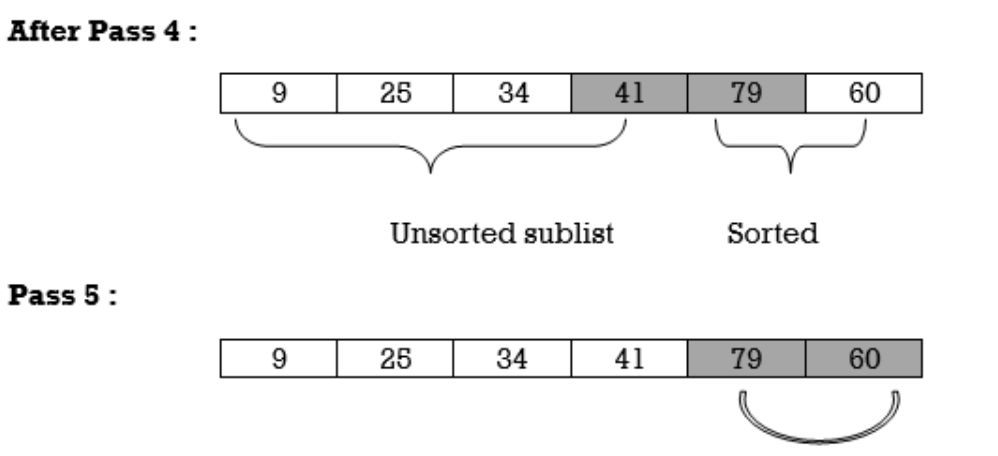
Pass 3 : Find the position P of the smallest in the sublist of N–2 elements A[3], A[4], . . . , A[N], and then interchange A[P] and A[3]. Then: A[l], A[2] , A[3] is sorted.
Pass N –1 :Find the position P of the smaller of the elements A[N –1), A[N], and then interchange A[P] and A[N–1]. Then: A[l], A[2], . . . , A[N] is sorted. Thus A is sorted after N –1 passes.
Example :
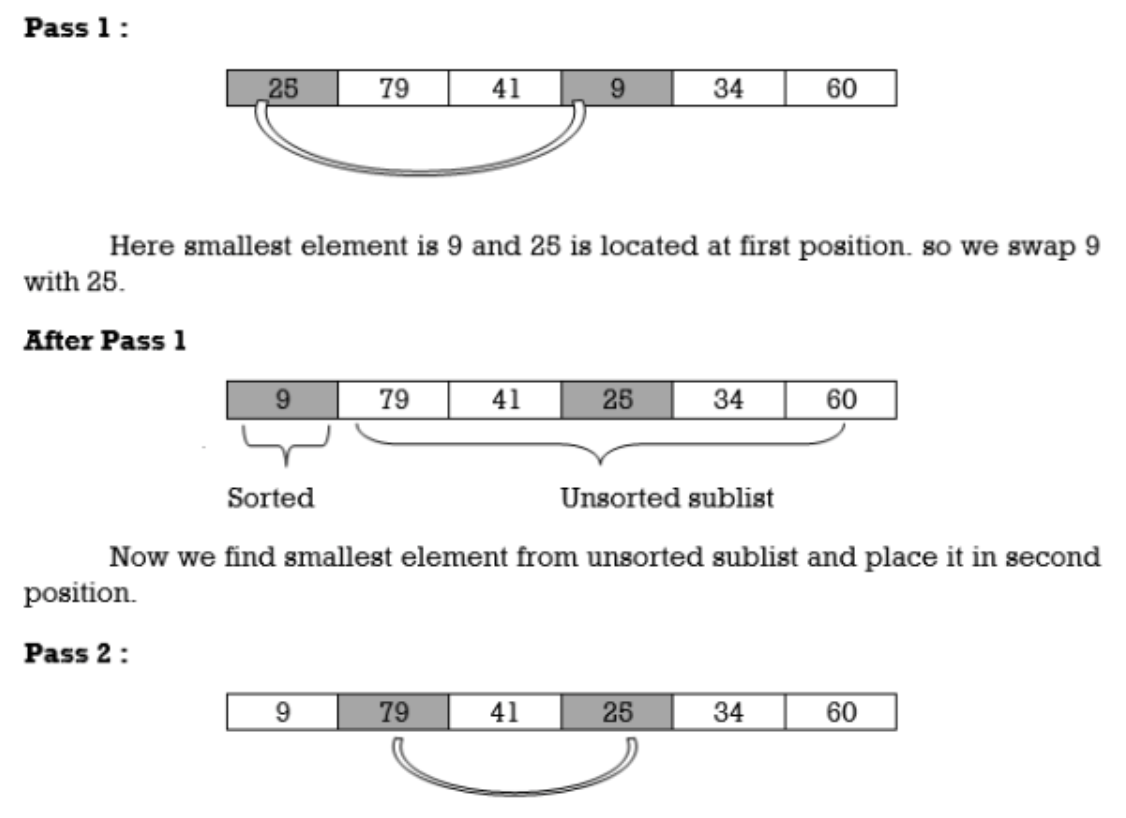
25 | 79 | 41 | 9 | 34 | 60 |
Fig 2: Original List
We will apply selection sort on this list.
|
Unsorted sublist has 25 as a smallest element and 79 is located at second position. Hence we swap 25 and 79.
|
|
After Pass 5 :
9 | 25 | 34 | 41 | 60 | 79 |
Thus the list is sorted.
Q.14) Write Concepts of time and space complexity ?
Ans : Concepts of time and space complexity
Time Complexity is a function that depicts the amount of time required for an algorithm to run before it is completed. The method you take in determining who has the book in the aforementioned scenario can be interpreted by time complexity. In computer science, however, this usually refers to how long the processes and data structures in our codebase / functions take to complete their task.
Time complexity, on the other hand, is a catch-all word for the various forms of time complexities that can be calculated. They are, in order of fastest to slowest:
● Worst case time complexity : The maximum number of times an operation must be performed before it is completed.
● Average case time complexity : The average number of times the algorithm / code would take to complete.
● Amortized Running Time : It is the number of times the process would take when performed repeatedly for a reasonable period of time, similar to average.
● Best case time complexity : The shortest time it takes for an operation to end.
Space complexity
Space Complexity is a feature that depicts the amount of space required for an algorithm to run until it is completed. In computer science, however, this usually refers to how much memory the processes and data structures in our codebase / functions use in order to achieve their target.
Importance of time and space complexity
Developers of real-world software are constrained by the physical memory of the systems they expect to operate on. This is where resource complexity comes into play, as we never want to run a feature or method that consumes more space than the system has available at any given time. On the other hand, we don't want our functions to take so long that they bog down and slow down our applications.