Unit - 2
Solution of First and Second order networks
Q1) For the circuit given below Find V0 (t) for t =o if capacitor is uncharged?

A1) Finding Req
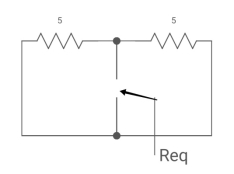
Fig. Circuit for Req
Req = R1R2 /R1+R2
V0(0) =0
V0 (infinity) = VR R2/R1+R2
V0 (t) = V0 (infinity) + [Vo (0) – V0 (infinity)] e-t/c
=VR R2/R1+R2 *[ 1- e+(R1+R2)/R1R2]
Q2) Find the value of V0(t) for circuit below?
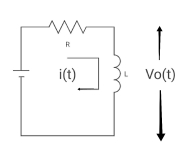
A2)
Time constant, c= L/Req = L/R
V(infinity) = 0
V (0) = VR
I(infinity) = VR/R, I (0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Q3) Find i(t) for the circuit below for t>0?
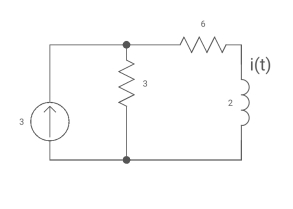
A3) The circuit for Req will be
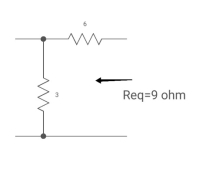
Fig. Circuit for Req
Req = 6+3
= 9ohm
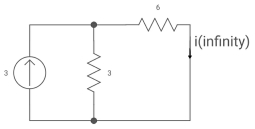
Fig. Circuit when inductor acts as short circuit
T= L/Req = 2/9 sec
I (0) =0
I(infinity) = 3*3/6+3 = 1A
i (+) = 1 [1-e4.51]
Q4) Capacitor is initially uncharged find Vc (t); t >0
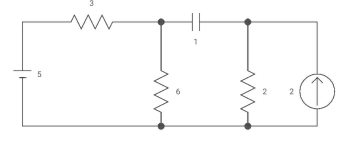
A4)
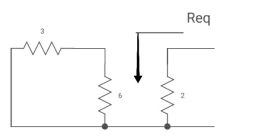
Fig. Circuit for Req
Req = (3116) +2
=2+2 = 4ohm
C= c Req
= 2 sec
Clearly Vc (0) =0
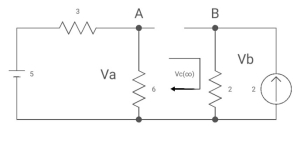
Fig. Circuit when capacitor acts as open circuit
By voltage divides, VA= 5*6/3+B = 30 v/9
Clearly by ohms low
VB = 2*2 = 4v
Apply KVL, VA-Vc-VB =0
Vc(infinity) = 30/9 – 4 = -2/3 V
Vc (t) = -2/3 [1- e0.5t]
CURVE:
:- 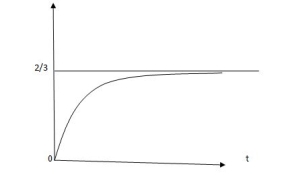
Vc(t) =2/3 [1-e-0.5t]

Fig. Response for above circuit
Vc(t) = -2/3 [1-e-0.5t]
Q5) Find i(t) for the given circuit below?
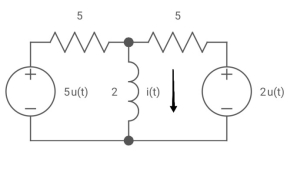
A5) We know i(t) = I (infinity) + [i (0)- i(infinity)] e-t/c
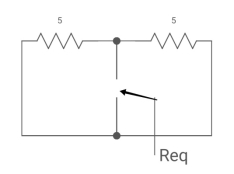
Fig. Circuit for Req
Req = 5*5/5+5 = 5?2 ohm
:. T=L/Req = 4/5 sec
Also, i (0) =0
i(infinity) = u(t) +2/5 u(t)
:. I(t) = 1.4 [1-e-5/4t)] u(t)
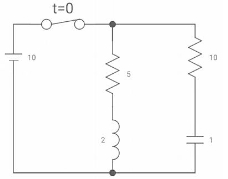
Q6) If switch ‘s’ closed at t= 0 find out the voltage across capacitor and current through capacitor at t= 0+?
A6) At t= 0- switch was open so,
:. There is no powntial so Vc (0-) = 0
At t= 0+, Vc (0-) = Vc (0+) = 0
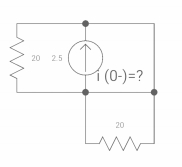
Isc = 10/5 = 2 A
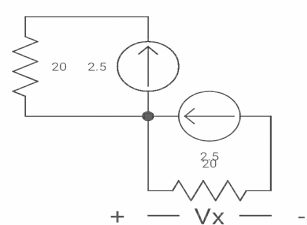
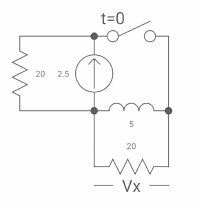
Q7) The switch was closed for long time before
Opening at t=0- find VX (0+)?
(a) 25V (b) 50 V (c)-50V (d) 0V
A7) At time t=0-
clearly, il (0-) = 2.5 A
at t= 0+, as inductor is initially charges
so il (0-) = il (0+)
-VX= 20/2.5 20*2.5
VX= -50A
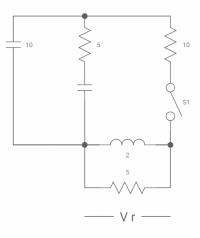
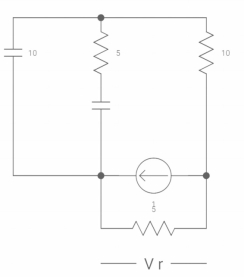
Q8) Find VR (0+) and dil/dt(t) = 0+ If switch is opened at t= 0?
A8)
At t=0-
Vc (0-) = 10V
IL (0-) = 10/10 = 1 A
Also, iL (0-) = iL (0+) = 1A
VR (0+) = 5V
Ldi(t)/dt = VL (t)
DiL(t)/dt = VL(t)/L
At t= 0+
d/dt iL (0+) = VL (0+)/L
-VL (0+)-VR =0
VL (0+) = -5V
dt(t) at t = ot = vl (ot)/L
=-5/2
dil/dt(o+) = 2.5 A/s
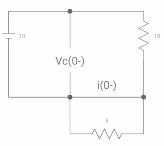
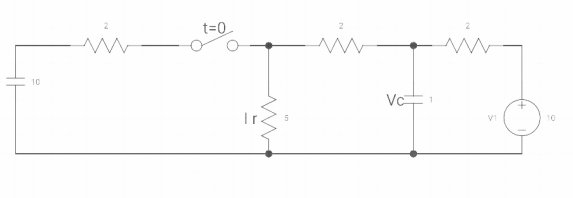
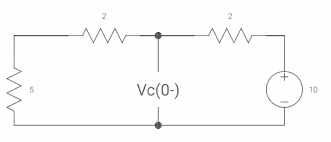
Vc(o+) and iR (o+) it switch ‘s’ is closed at t=0?
At t=0
As capacitor is fully charged so acts as
Vc (0-) = 7*10/7+2 = 70/9v
At t=0+
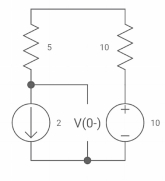
Vc (0+) = Vc (0) = 40/9v
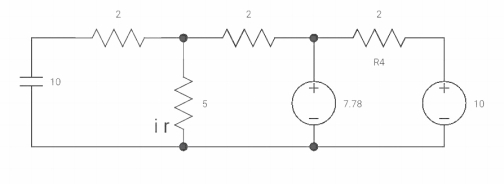
By applying kcl at A,
VA-10/2+ VA/5+VA-7019/2 =0
VA [1/5+! /2+1/2] = 5+35/9
Va [6/5] = 80/9
Va= 400/54v
IR (0+) = va/5 = 400/54*5 = 80/54 A
Q9) Derive the time constant for RC circuit?
A9) FOR RC Circuit
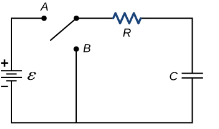
Fig. Series RC circuit
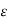 =V
=V
For t>0 applying KVL
Ri(t)+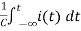 +V=0
+V=0
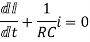
Hence general solution of above equation is calculated same as for RL circuit
i=k
i (0) =- 
Hence, particular solution for network is given as
i=-  for t≥0
for t≥0
= for t<0
for t<0
The time constant is given as 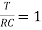
T=RC
Q10) Write the equation for complete solution of a differential equation?
A10) The complete or total response of network is the sum of the transient response and steady state response which is represented by general solution of differential equation.
First order homogenous differential equation.
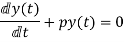

Integrating both sides
y(t)=k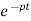
First order non homogenous differential equation
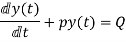

Integrating above equation we get
y(t) =∫ Q
=∫ Q 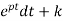
y(t)=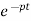 ∫ Q
∫ Q 
The first term of above solution is known as particular Integral and second is known as complementary function.