Unit - 4
Electrical Circuit Analysis Using Laplace Transforms
Q1) For given RL circuit find the differential equation for current i?
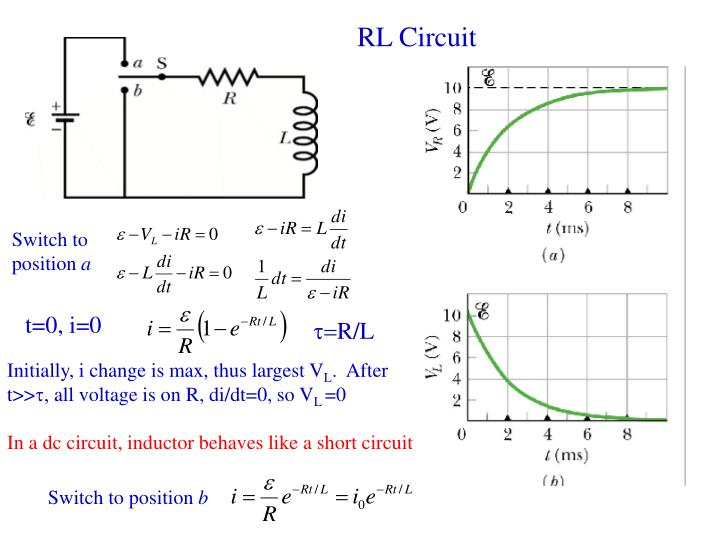
Fig1: Series RL circuit
A1) After switch is closed applying KVL
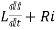 =0
=0
This is first order homogeneous differential equation so
 dt
dt
Integrating both sides
ln i=  t+K
t+K
taking antilog of both sides
i=k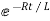
At t=0
i (0) = =I0
=I0
 =ke0
=ke0
The particular solution is given as
i= 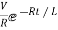 for t≥0
for t≥0
= for t<0
for t<0
Q2) Find IL (0) for the given circuit below
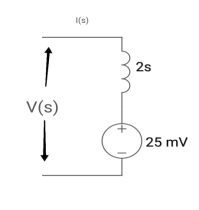
A2) From above circuit
L = 2H
LiL (0) = 25 mv
IL (0) = 12.5 m A
Q3) Find value across capacitor?
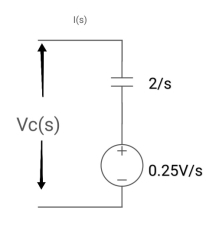
A3) From above circuit we can write
1/cs = 2/s
C=1/2f
Vc (0)/s = 0.25v/s
Vc (0) = .25v
Q4) Find voltage across capacitor?
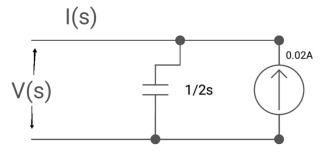
A4) 1/cs = 1/2S
C=2F
CVc (0) = 0.02
Vc (0) = 0.01V
Q5)
(a) switch is at before moving to position = at t= 0, at t= 0+, i1(t) is
(b) –V/2R (b) –V/R (c) – V/4R
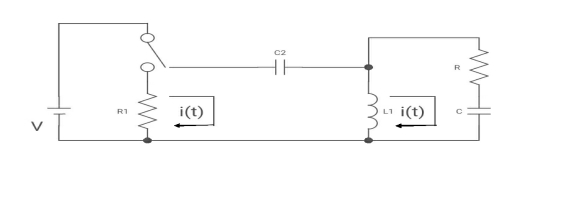
A5)
I1(t) L.T I1(s)
I2(t) L.T I2(s)
then express in form
[ I1(s)/I2(s)] [:] = [:]
Drawing the ckl at t = 0-
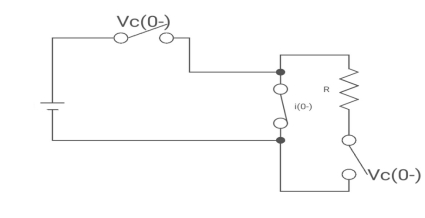
:. The capacitor is connected for long
Vc1(0-) = V
iL (0-) =0
Vc2(0-) =0
at t= 0+
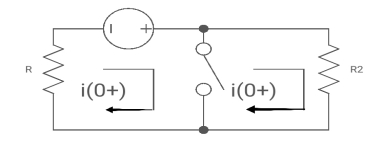
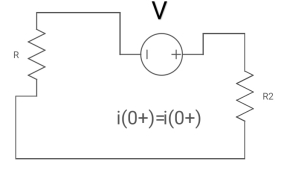
i1 (0+) = -V/2R
for t>0 the circuit is
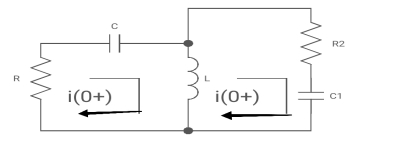
Apply KVL
-R i1(t) -1/c 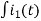 dt -L
dt -L =0
=0
Also, we can deduce i1(t)- i2 (t) = iL(t)
-Ri1(t) -1/c 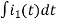 - L
- L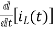 = 0
= 0
-RI1(s)-[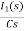 -
-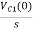 ]-L[sI1(s)-iL (0-)] =0
]-L[sI1(s)-iL (0-)] =0
- RI1(s)-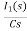 -
-  -s L I2(s)=0
-s L I2(s)=0
 - s L I2(s)= -
- s L I2(s)= -  (1)
(1)
Again
-Ri2(t)) -1/c 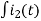 dt -L
dt -L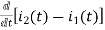 =0
=0
-Ri1(t) -1/c 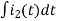 - L
- L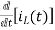 = 0
= 0
Taking Laplace Transform
-RI2(s)- [ -
-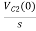 ]- L [s IL(s)- iL (0-)] =0
]- L [s IL(s)- iL (0-)] =0
-RI2(s)- 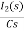 -
- Ls [ I1(s)- I2(s)] =0
Ls [ I1(s)- I2(s)] =0
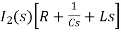 - s L I1(s)=0 (2)
- s L I1(s)=0 (2)
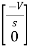
Hence in matrix representation

 =
= 
Q6) All initial conditions are zero i(t) L.T, I(s), then find I(s)?
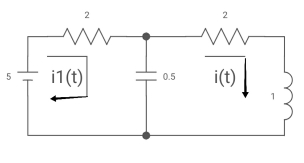
A6) Drawing Laplace circuit
(2+S) 11 2/S
Zeq = [(2+S)2/S]/[2+S+2/S] =[2(S+2)]/[S2+2s+2]
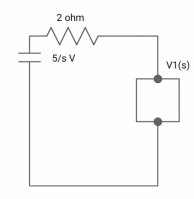
V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]
V1(s) = [5(S+2)/S]/ [S2+ 3S +4]
I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)
Q7) Write equation for given waveform
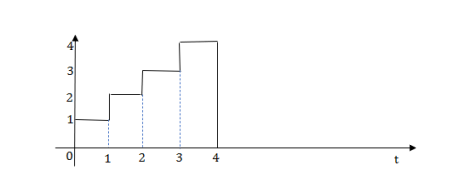
A7)

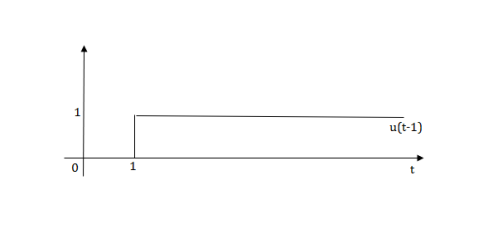


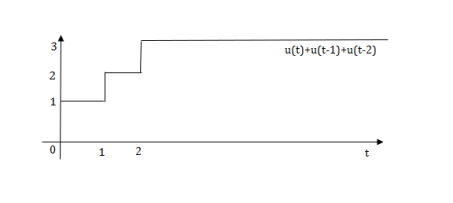

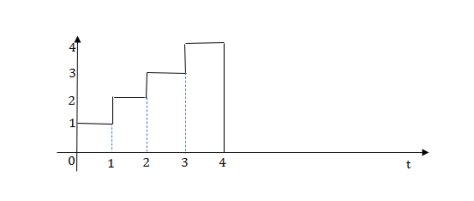
The final equation is=u(t)+u(t-1) +u(t-2) +u(t-3)-4u(t-4)
As the waveform is stopped at t=4 with amplitude 4, so we have to balance that using -4u(t-4).
Q8) Write the equation for the given waveform?

A8) Calculating slope of above waveform
Slope for (0,0) and (1,2)
a1 slope=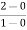 =2
=2
a2 slope=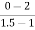 =-4
=-4

a3 slope =4 and a4= -2

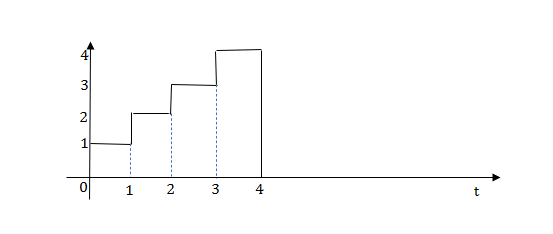
At t=1 slope changes from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.

At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4

At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence, we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as 2r(t)-6r(t-1.5) +8r(t-1.5)-6r(t-2) +2r(t-3)
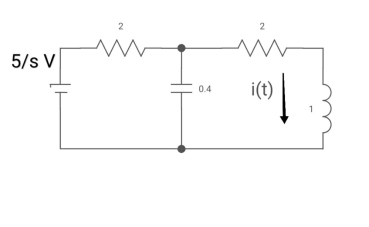
Q9) All initial conditions are zero i(t) I(s), then find I(s)?
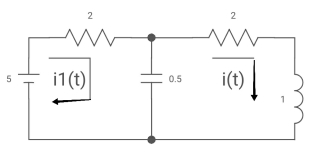
A9) Drawing Laplace circuit

(2+S) 11 2/S
Zeq = [(2+S)2/S]/[2+S+2/S] =[2(S+2)]/[S2+2s+2]
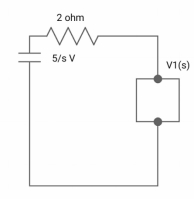
V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]
V1(s) = [5(S+2)/S]/ [S2+ 3S +4]
I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)
Q10) A series RL low-pass filter cut-off frequency is 2KHz. R=5KΩ Find the inductor value. Find |H(jω) | at 50 KHz?
A10) The cut-off frequency is 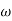 c = R/L
c = R/L
L= 5000/2000 =2.5Hz
|H(jω) | = 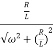
Substitute values in above equation for 50KHz we get
|H(jω) | = 0.0635
Q11) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
A11) The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 
= 3ohm
cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Q12) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
A12) R=V/I= 4.5/8 = 0.56ohm
At 25Hz, Z= V/I=24/8 =3ohms
XL = 
= 2.93ohm
XL = 2 fL = 2
fL = 2 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z =  = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Q13) A coil having inductance of 50mH an resistance 10ohmis connected in series with a 25 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
A13) f0= = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Q14) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
A14) XL = 2 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/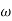 C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Q15) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
A15) For series Z =100/0.8 = 125ohm
cosφ = 
R = 0.3 x 125 = 37.5ohm
XL = 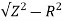 = 119.2ohm
= 119.2ohm
XL = 2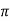 fL = 2
fL = 2 x 50x L
x 50x L
119.2 = 2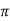 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2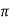 x50 = 0.417H
x50 = 0.417H