Unit - 5
Two Port Network and Network Functions
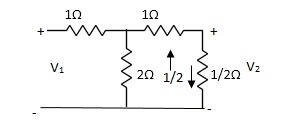
Q1) For the network shown below 1) show that with port 2) open the driving point input impedance 1π) b) find the voltage, ratio transfer function 1/2 for the two-port network.
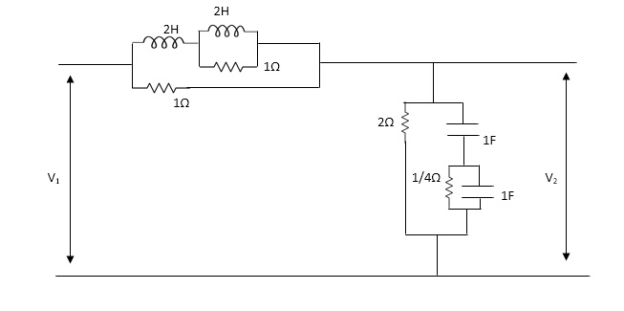
A1) From above network we take L.T
Fig 1 Laplace Transform for above circuit
Reducing we get,
Z1= (25+25*1 / 25+1) *1
25+25*1 / 25+1*1
Z1=4S2+45/452+65+1
Z2=(1/4S/1/4+1/5+1/5) *2=1/45/1/4+1/3+1/5+2
=2(5+5+4) / 5+5+4+25(5+4) = 2(25+4)/252+10S+4
Z2=25+4/252+10+4
Applying KVL, in the circuit
V1=I1Z1+I, Z2 -----------1
V2= I1Z2 ...............2
.: V1=I1Z1+V
V1 / I1= (Z1+Z2) (from----1)
Dividing equation 2 by 1
G12=Z 2 / Z1+Z2
calculating z11 we have,
Z11=Z1+Z2
Z11 = 4S2+4S / 4S2+6S+1 * 2S+4/S2+SS+2
=(4S2+4S) (S2+SS+2) +(2S+4) (4S2+6S+1) / (4S2+6S+1) (S2+SS+2)
Z11=4S4+20S3+8S2+4S3+20S2+8S+8S3+12S2+25+16S2+4 /(4S2+6S+1) (S2+SS+2)
= (4S4+32S3+5652+345+4 / (4S2+6S+1) (S2+SS+2)
G12= Z2 / Z1+Z2
= (2S+4) / (S2+SS+2) / (4S+32S3+56S2+34S+4) / (4S2+6S+1) (S2+SS+)
G12= (2S+4) (4S2+6S+1) / 4S4+32S3+56S2+34S+4
Q2) For the network shown, find driving point input impedance. plot the pole zero pattern for each as well
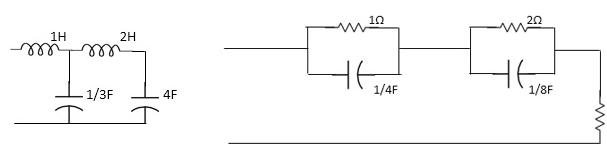
Fig 2 (1) Circuit Diagram Fig 2(2) Circuit Diagram
A2): From Fig 2(1) taking L.T we have
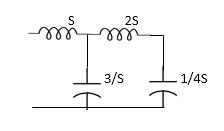
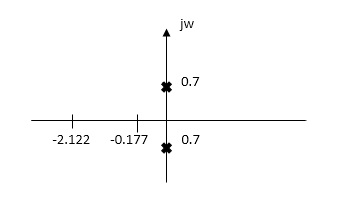
Fig 3 Laplace for Fig 2(1) with roots
Z11= 1+ 1 /S/3+1/25+1/1/4S
=1+ 1/ 5/3+1/6S
=1+ 18S/6S2+3
Z11=6S2+3+18S/ 6S2+3 =2S2+6S+2/2S2+1
Zeros of equations are taking lt. of circuit b)
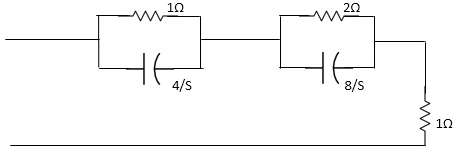
Fig 4 Laplace for Fig 2(2)
Z11= 1*4/5
=1+4/5+2.8/3/2+8/5+1
=4/5+4 + 16/ 25+8+1
= 4/5+4+8/5+4+1
=s+12+4/ (5+4)
Z11= S+16/(S+4)
For zeros of system
s+16=0
s=-16
for poles of system
s+4=0
s=-4
Q3) Find Z-parameter
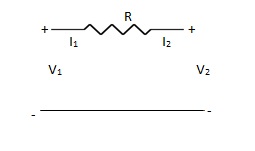
A3) I1 = -I2
Current dependent so Z-parameter doesn’t exist
Q4) Find z-parameter
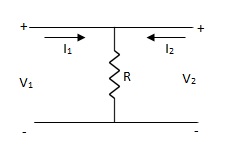
A4) V1 =R (I1 + I2)
V2 = R (I1 + I2)
Z11 = Z12 = Z21 = Z22 = R
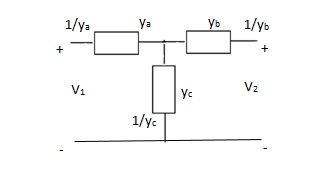
Q5) Find z-parameter?
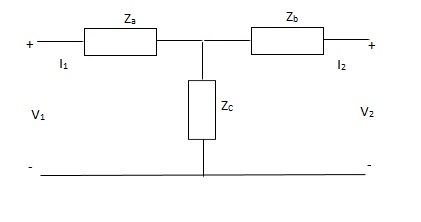
A5) V1 = I1Za + I1Zc + I2Zc
= (Za + Zc) I1 + ZcI2
V2 = I2Zb + I2Zc + I1Zc
= (Zb + Zc) I1 + ZcI1
Z11 = (Za + Zc)
Z12 = Zc = Z21
Z22 = (Zb + Zc)
Q6) Find z-parameter?
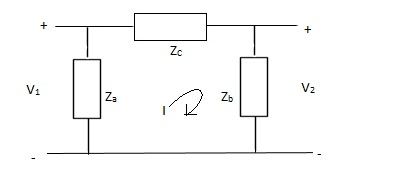
A6) V1 = Za (I1 - I)
(I - I1) Za+ IZc+ Zb (I + I2) = 0
I (Za + Zb + Zc) – I1Za + I2Zb = 0
I =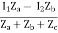 
V1 = ZaI1 - Za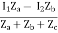
= 
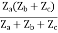I1 + I2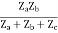 
V2 = Zb (I2 + I)
= ZbI2 + Zb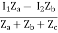
= 
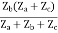I2 + I2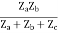 
Z11 =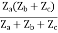 
Z12 = Z21 =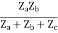 
Z22 = 
Q7) Find z parameter using conversion?
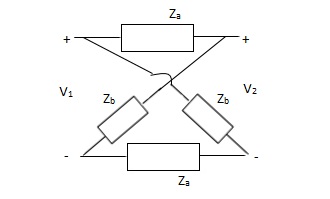
A7)
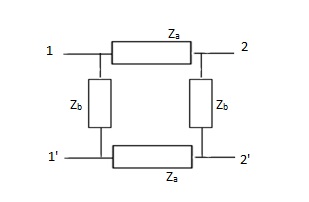
Z11 = 
I2=0
V1 -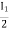 
(Za + Zb) = 0
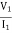= Z11 =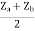 
Z21 = 
I2=0
V2 -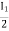 
Zb +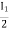
Za = 0
= 
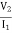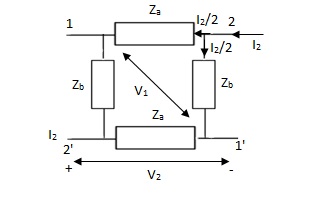
Z12 =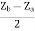 
Z22 =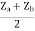 
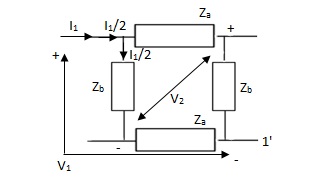
Q8) Find Z21?
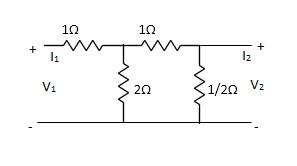
A8) Z21 =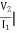 
I2=0
I1/2 =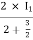 
= 
I1
V2 = 
I1/2
= 
× 
I1
= 
I1
Z21 =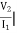 
I2 = 0 = 
I1 Ω
Q9) Find overall Y-parameter?
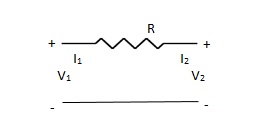
A9) V1 – I1R – V2 = 0
V1 – V2 = I1R
I1 = 
V1 - 
V2
V2 = I2R + V1
I2 = - 
V1 + 
V2
Y11 = 
Y12 = Y21 =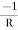 
Y22 = 
The over all Y parameter is given as 
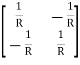
Q10) Find overall Y-parameter
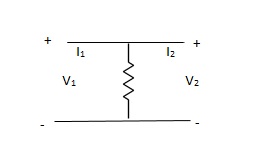
A10) Y-parameter does not exist as V1 = V2
Q11) Find overall Y-parameter?
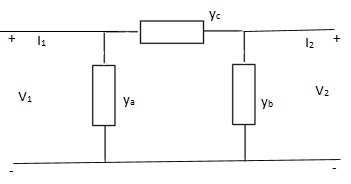
A11) I1 = V1Ya + (V1 – V2) Yc
I1 = (Ya + Yc) V1 - YcV2
I2 = V2Yb + (V2 – V1) Yc
I1 = (Yb + Yc) V2 - YcV1
Y11 = Yb + Yc
Y12 = Y21 = - Yc
Y22 = Yb + Yc
Q12) Find overall Y-parameter?
A12)
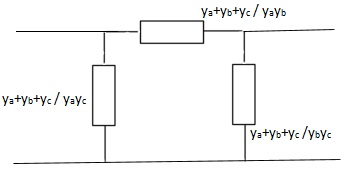
The overall y parameter is given by
Q13) Find all the Transmission parameters?
A13)
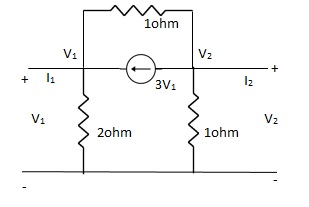
-3V1 – I1 +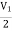 
+ 
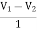= 0
+ 
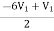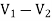= I1
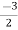V1 – V2 = I1
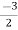V1 = V2 + I1
V1=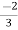
V2-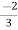 
I1----------------(1)
I2 = 3V1 + V2 + V2 – V1
I2 = 2V1 + 2V2
2V1 = I2 - 2V2
2V1 = - 2V2 + I2
V1 = -V2 + 
I2 ----------------(2)
A = -1
B = 
From (1) & (2)
-V2 + 
I2 = 
I1 - 
V2
V2 - V2 + 
I2 = 
I1
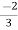I1 =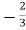 
V2 + V2 - 
I2
I1 = 
V2 - 
I2
C = 
D = 
Q14) Find all the Transmission parameters?
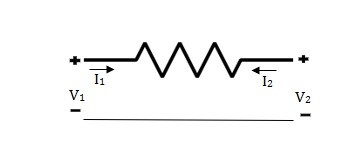
A14) V1 = RI1 + V2 ----------------(1)
I2R = V2 – V1
I2 = 
V2 - 
V1
I2R = V2 – V1
V1 = I2R - V2 --------------------(2)
A = 1
B = R
From (2) in (1)
V2 - I2R = V2 + RI1
I2 = -I1
C = 0
D = 1
Q15) Find all the Transmission parameters?
A15) V1 = R (I1 + I2)
V2 = R (I1 + I2)
V1 = V2 + 0I2
A = 1
B = 0
V2 = RI1 + RI2
RI1= V2 - RI2
I1 = 
V2 – I2
C = 
, D = 1
Q16) Find all h-parameter?
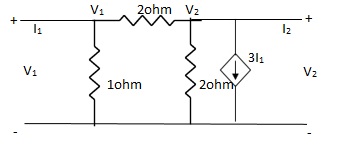
A16)
+ 
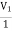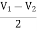= I1
V1 - 
= I1
V1 = 
+ I1
V1 =
+ 
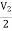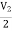I1
- 
+ 3I1 = I2
3I1 + V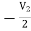2
= I2
From (1)
I2 = 3I1 + V2 – 
[
I1 + 
V2]
I2 = 
I1 + 
V2
h11 = 
h12 = 
h21 = 
h22 = 
Q17) Find out overall transmission parameter?
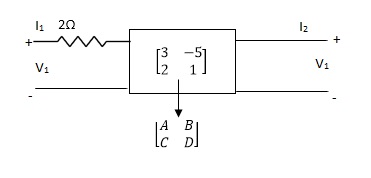
A17)
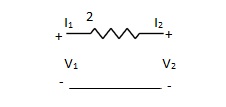
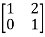
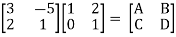
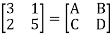
Q18) Find overall Y-parameter?
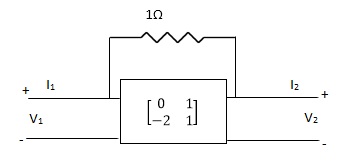
A18)
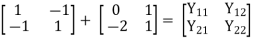
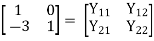
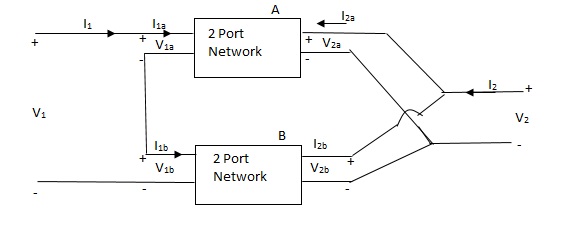
Q19) Explain the series parallel connection of two port network. Derive the equations of h-parameter for the network?
A19)
I1 = I1a = I1b
V1 = V1a +V1b
If two 2-ports are connected in series parallel then overall h-parameter is sum of individual h-parameter
= 
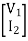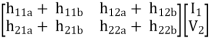
Q20) When the two-port network are connected in series which parameter is calculated. Derive and explain?
A20)
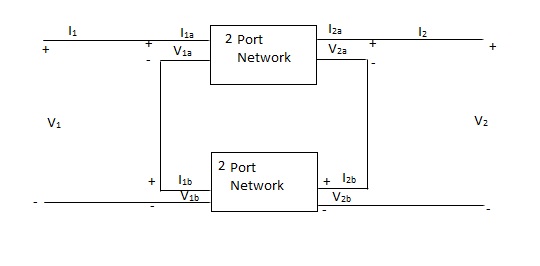
V1 = V1a +V1b
I1 = I1a = I1b
V2 = V2a +V2b
I2 = I2a = I2b
= 
= 
= 
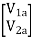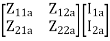
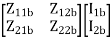
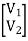