Unit - 1

Review of First and Second laws

Q1) Explain the First Law of Thermodynamics

A1) The first law makes use of the key concepts of internal energy, heat, and system work. It is used extensively in the discussion of heat engines. The standard unit for all these quantities would be the joule, although they are sometimes expressed in calories or BTUs.

It is typical for chemistry texts to write the first law as ΔU=Q+W. It is the same law, of course - the thermodynamic expression of the conservation of energy principle. It is just that W is defined as the work done on the system instead of work done by the system. In the context of physics, the common scenario is one of adding heat to a volume of gas and using the expansion of that gas to do work, as in the pushing down of a piston in an internal combustion engine. In the context of chemical reactions and processes, it may be more common to deal with situations where work is done on the system rather than by it.

∆U = Q – W

∆U = change in internal energy

Q = Heat add to system

W = work done by system

The second law of thermodynamic is a general principle which place constraints upon the direction of heat transfer and the attainable efficiencies of heat engines.in so doing it goes beyond the limitation implications may be visualized in terms of the waterfall analogy.

Q2) Explain the second Law of Thermodynamic

A2) The second law of thermodynamic is a general principle which place constraints upon the direction of heat transfer and the attainable efficiencies of heat engines.in so doing it goes beyond the limitation implications may be visualized in terms of the waterfall analogy.

Second Law of Thermodynamics: It is impossible to extract an amount of heat QH from a hot reservoir and use it all to do work W. Some amount of heat QC must be exhausted to a cold reservoir. This precludes a perfect heat engine.

This is sometimes called the "first form" of the second law, and is referred to as the Kelvin-Planck statement of the second law.

Q3) What is the Limitations of First Law of Thermodynamics

A13) First law of thermodynamics that - When a closed system undergoes a thermodynamic cycle, the net heat transfer is equal to the net work transfer. This statement does-not specify the direction of flow of heat and work (i.e., whether the heat flows from a hot body to a cold body or from a cold body to a hot body). It also does not give any condition under which these transfers take place.

 2 The heat energy and mechanical work are mutual!) convertible. Though the mechanical work can be fully converted into heat energy, but only a part of heat energy can be converted into mechanical work. This means that the heat energy and mechanical work are not fully mutually convertible. In other words, there is a limitation on the conversion of one form of energy into another form.

A machine which violates the first law of thermodynamics (i.e., energy can neither be created nor destroyed, but can be transformed from one form to another) is known as perpetual motion machine of the first kind (briefly written as PMM-I). It is defined as which produces work energy without consuming a machine of the first kind. equivalent of energy from other source. Such a machine, as shown in Fig. 1. 10, is impossible to obtain in actual practice, because no machine can produce energy of its own without consuming any other form of energy.

Q4) What is the Steady flow processes?

A4) Rates of flow of mass, energy is constant across the system boundary – e.g., Turbines, compressors, heat exchangers etc

Energy analysis of steady flow systems:  Several engineering devices can be approximated to operate as steady flow devices: turbine, compressors, nozzles etc.

• During a steady-flow process, no intensive or extensive properties within the control volume change with time.

• The boundary work is zero for steady-flow systems (since VCV =constant).

• The total mass or energy entering the control volume must be equal to the total mass or energy leaving it

Properties of steady flow processes

Q5) What is the Unsteady flow processes?

A5) In an unsteady flow process, mass and energy within the control volume vary continuously. The fluid flow into and out of the system.

Example: Filling or evacuation of a tank, (internal energy as well as mass of the tank changes with time), the condition of water in the cylinder jacket of an I.C. engine (is time dependant)

Q6) Explain the Analysis of unsteady flow system

A6) Consider the flow of a fluid through a pipe line into the cylinder. Let m1 be the mass of the fluid initially in the cylinder at pressure p1, temperature t1 and m2 the final mass in the cylinder at pressure p2, temperature t2. The mass that flows into the cylinder is thus (m2 – m1).

There are two ways for solving problems involving unsteady flow (i) Closed system analysis (ii) Control volume analysis

Since no mass crosses the boundary of the system, the boundary of the system is selected in such a way that it includes not only the cylinder but also that portion of the fluid in the pipe line which will be introduced eventually into the cylinder as shown in figure. That means the system has variable boundaries which at the final state will be the same as that of the cylinder. Initially energy of the system E1 is composed of the internal energy of the mass initially in the cylinder, m1u1 plus the energy of the fluid which will eventually flow the pipe line into the cylinder, (m2 – m1) where the subscript ‘p’ refers to the condition of the fluid in the pipe line. At the final state, energy E2 of the fluid in the system will be equal to m2u2.

Neglecting the change in PE, the change in energy is, the pipe line into the cylinder, (m2 – m1) where the subscript ‘p’ refers to the condition of the fluid in the pipe line. At the final state, energy E2 of the fluid in the system will be equal to m2u2.

Neglecting the change in PE, the change in energy is,

The cylinder itself is taken as the control volume as shown in figure. In this case, there is no work interaction. Using the general equation 1st law and considering no mass flows out of the control volume and neglecting the change in PE, as in the earlier case we have

If the tank would have been thermally insulated and initially empty, and substituting into equation (1) and simplifying, we get

Also, if KE in the pipe line is not appreciable, hp = u2 i.e., the specific enthalpy of the fluid in the pipe line is equal to the specific internal energy of the fluid in the cylinder at the final state.

Q7) A household gas cylinder initially evacuated is filled by 15 kg gas supply of enthalpy 625 kJ/kg. After filling, the gas in the cylinder has the following parameters: pressure 10 bar, enthalpy 750 kJ/kg and specific volume 0.0487 m3/kg. Evaluate the heat received by the cylinder from the surroundings.

A7)

Where is the specific volume of the fluid in the pipeline.

Applying 1st law thermodynamics,

But

Above equation becomes,

(ii) Control volume analysis:

Q8) Explain Mass and Energy Balance for Steady-flow Process

A8) The conservation of mass principle, which has been previously introduced, in rate format, is:

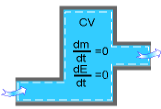
During a steady-flow process, the total amount of mass contained within a control volume does not change with time. That is,

dmsystem/dt = 0

Hence the conservation of mass principle gives the total amount of mass entering a control volume equal to the total amount of mass leaving it. In an equation format, it is

Mass and Energy balance for Steady-flow Process

(Total mass entering the control volume per unit time) =

(Total mass leaving the control volume per unit time)

Also, the energy balance for a process, which has been previously introduced, in rate format, is:

For a steady-flow process, the total energy content of a control volume remains constant. That is,

dEsystem/dt = 0

Thus, the amount of energy entering a control volume in all forms (heat, work, mass transfer) must be equal to the amount of energy leaving it for a steady-flow process. In an equation format, it is

(Rate of net energy transfer in by heat, work and mass) =

(Rate of net energy transfer out by heat, work and mass)

or,

 For a general steady-flow process, the energy balance can be written as

If the sign introduced previously for heat and work is used, the energy balance for a general steady-flow process can be rewritten as:

Q9) A line AB 60 mm long has its end 20 mm above HP and 30 mm in front of VP. The line is kept perpendicular to HP and parallel to VP. Draw its projections. Also mark the traces.

A9)

Given:

SFEE to filling process is

The cylinder is initially evacuated also

Q10) An insulated and rigid tank contains 5 m3 of air at 10 bar and 425 K. The air is then let off to atmosphere through a valve. Determine the work obtainable by utilizing the KE of the discharge air. Take Cp = 1 kJ/kg K, CV = 0.714 kJ/kg0-K atmosphere pressure = 1 bar.

A10)

The situation corresponds to emptying process, for which the energy balance equation is,

Insulated and rigid tank

Q11) Explain the Entropy

A11) In other words the integral remains the same no matter what the path is. It can be simply written as S 2-S1. The value depends only on the end states and not on the path followed. So, it is a state function or a property. ™ Like energy entropy (s) is also an extensive property. It will have the units of J/K. Similar to energy where we converted it into specific property, specific entropy (lower case s) will have units of J/kg K (same as specific heat)

∫2 δQ /T= S 2-S 1 or 1 ∫2 δq /T= s 2-s 1 ⏐ δq /T= δs or δq = T δs

Integrals under P-V plane give work interaction   ™Integrals under T-S plane give heat interactions