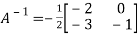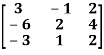UNIT-1

Matrices

Question-1: Find the rank of a matrix A by echelon form.

A =

Sol. Convert the matrix A into echelon form,

A =

Apply 

A =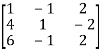

Apply 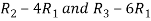   , we get

A =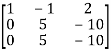

Apply 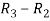, we get

A =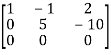

Apply ,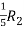

A =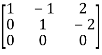

Apply  ,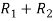

A =

Therefore the rank of the matrix will be 2.

Question-2: Find the rank of the following matrices by echelon form?

Let A =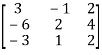

Applying

A 

Applying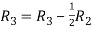

A 

Applying

A 

      Applying

A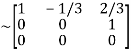 

It is  clear  that  minor  of order 3  vanishes but  minor  of order  2  exists  as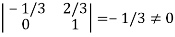 

Hence rank of a given matrix A is 2 denoted by 

2.    

Let  A  = 

Applying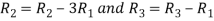

Applying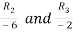

Applying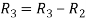

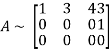
The minor of   order   3 vanishes but minor of order 2 non zero as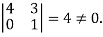 

Hence the rank of matrix A is 2 denoted by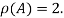

3.    

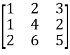
Let A =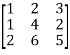

Apply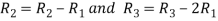

Apply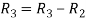

Apply

It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as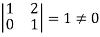 

Hence the rank of given matrix is 2 i.e.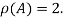

Question-3: Reduce the matrix A to its normal form and find rank as well.

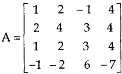
Sol.  We have,

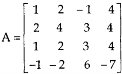
We will apply elementary row operation,

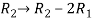
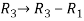
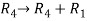
We get,

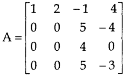
Now apply column transformation,

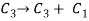
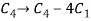
We get,

Apply

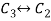  , we get,

Apply 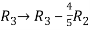  and

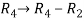
Apply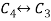 

Apply 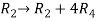  and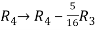

Apply 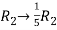  and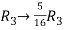

As we can see this is required normal form of matrix A.

Therefore the rank of matrix A is 3.

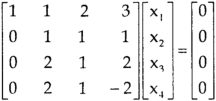
Question-4: Find the solution of the following homogeneous system of linear equations,

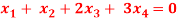
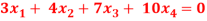
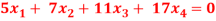
Sol. The given system of linear equations can be written in the form of matrix as follows,

Apply the elementary row transformation,

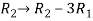
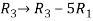
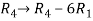  , we get,

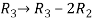
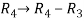    , we get

  Here r(A) = 4, so that it has trivial solution,

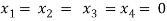
Question-5: : Check the consistency and find the values of x , y and z of the following system of linear equations.

2x + 3y + 4z = 11

X + 5y + 7z = 15

3x + 11y + 13z = 25

Sol. Re-write the system of equations in augmented matrix form.

                                  C = [A,B]

That will be,

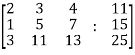
Apply 

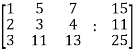
Now apply ,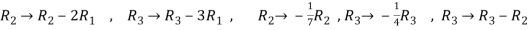

We get,

~~

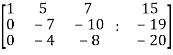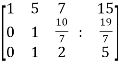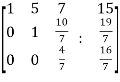
Here rank of A = 3

And rank of C = 3, so that the system of equations is consistent,

So that we can can solve the equations as below,

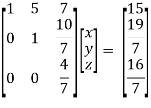
That gives,

x + 5y + 7z = 15  ……………..(1)

y + 10z/7 = 19/7 ………………(2)

4z/7 = 16/7 ………………….(3)

From eq. (3)

z = 4,

From 2,

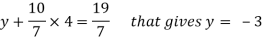
From eq.(1), we get

x + 5(-3) + 7(4) = 15

That gives,

x = 2

Therefore the values of x , y , z are    2 , -3 , 4  respectively.

Question-6: solve the following system of linear equations by using Guass seidel method-

6x + y + z = 105

4x + 8y + 3z = 155

5x + 4y  - 10z = 65

Sol. The above equations can be written as,

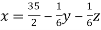   ………………(1)

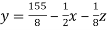………………………(2)

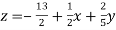   ………………………..(3)

Now put z = y = 0 in first eq.

We get

x = 35/2

Put x = 35/2 and z = 0 in eq. (2)

We have,

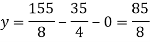
Put the values of x and y in eq. 3

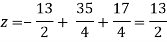
Again start from eq.(1)

By putting the values of y and z

y = 85/8 and z = 13/2

We get

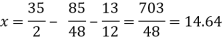
The process can be showed in the table format as below

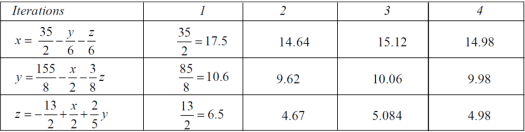
At the fourth iteration , we get the values of x = 14.98 , y = 9.98  , z = 4.98

Which are approximately equal to the actual values,

As x = 15  , y = 10 and  y = 5 ( which are the actual values)

Question-7: : check whether the following matrix A is symmetric or not?

A = 

Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.

So that, first we will find its transpose,

Transpose of matrix A ,

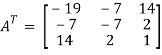
Here,

A =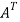

So that, the matrix A is symmetric.

Question-8: Are the vectors , , 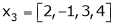linearly dependent. If so, express x1 as a linear combination of the others.

Solution:

Consider a vector equation,

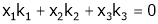
i.e.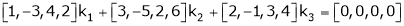

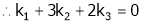
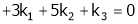
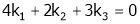
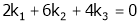
Which can be written in matrix form as,

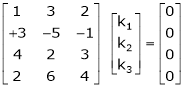
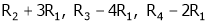
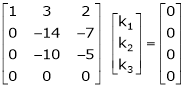
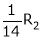
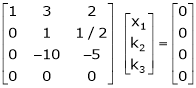
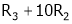
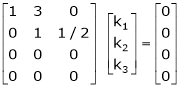
Here & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

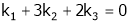
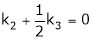
Put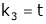

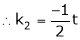and

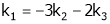
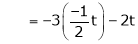
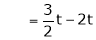
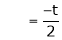
Thus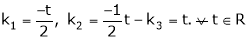

i.e.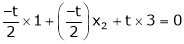

i.e.

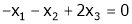
Since F11k2, k3 not all zero. Hence 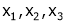are linearly dependent.

Question-9: Determine the Eigen values of Eigen vector of the matrix.

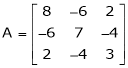
Solution:

Consider the characteristic equation as,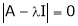

i.e.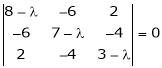

i.e.

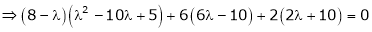
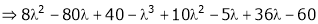
i.e.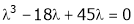

Which is the required characteristic equation.

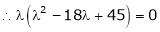
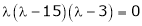
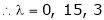are the required Eigen values.

Now consider the equation

… (1)

Case I:

If 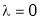Equation (1)becomes

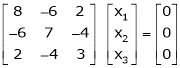
R1 + R2

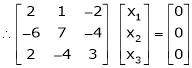
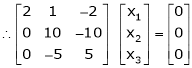
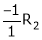
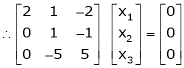
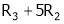
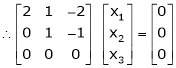
Thus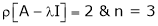

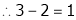independent variable.

Now rewrite equation as,

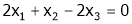
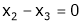
Put x3 = t

&

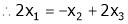
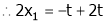
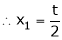
Thus .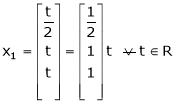

Is the eigen vector corresponding to .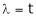

Case II:

If equation (1) becomes,

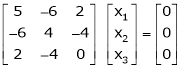
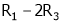
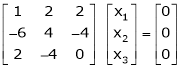
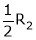
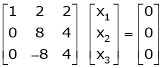
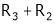
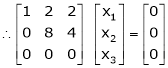
Here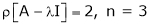

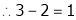Independent variables

Now rewrite the equations as,

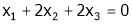
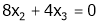
Put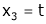

&

.

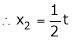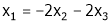
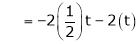
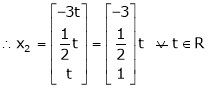Is the eigen vector corresponding to .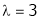

Case III:

If 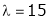equation (1) becomes,

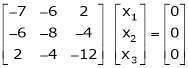
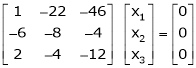
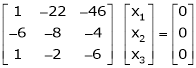
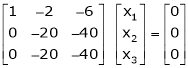
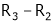
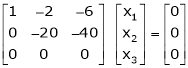
Here rank of

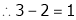independent variable.

Now rewrite the equations as,

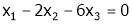
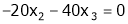
Put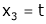

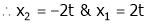
Thus .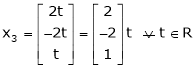

Is the eigen vector for .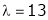

Question-10: Diagonalise the matrix

Let A=

The three Eigen vectors obtained are  (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .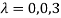

Then 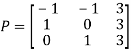   and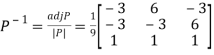

Also we know that    

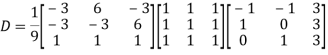
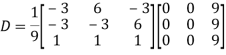
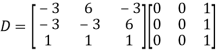
Question-11: Using Cayley-Hamilton theorem, find , if A = ?

Sol. Let A =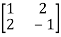

The characteristics equation of A is

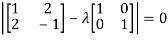
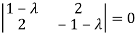
Or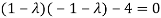

Or

By Cayley-Hamilton theorem   

L.H.S.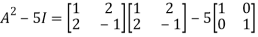

=

By Cayley-Hamilton theorem we have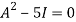   

            Multiply both side by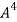

.

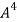
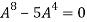
Or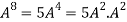 

=

=

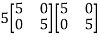
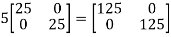
Question-12: Verify the Cayley-Hamilton theorem and find the inverse.

?

Sol.  Let A =

The characteristics equation of A is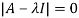

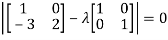
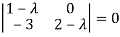
Or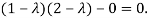

Or 

Or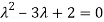 

By Cayley-Hamilton theorem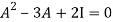 

                                   L.H.S: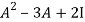

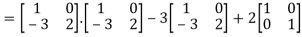
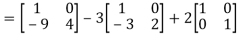
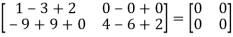                                                 =   =0=R.H.S

Multiply both side by 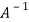on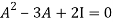 

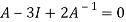
                                               Or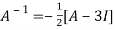

                                              Or [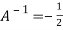

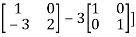
                                               Or