UNIT-4
UNIT-4
Partial differential equation: First order
Question-1: Find the differential equation of all circles touching the y-axis at the origin?
The equation of the circle that touches y-axis at the origin is
 ….(i)
….(i)
Differentiating (i) with respect to x, we get
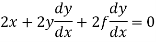
Or 
Or 
Or 
Or 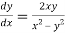
Or 
This is the required differential equation.
Question-2: Solve 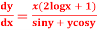
Solution. We have, 
Separating the variables we get
(sin y + y cos y )dy ={ x (2 log x +1} dx
Integrating both the sides we get 
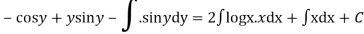

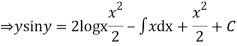
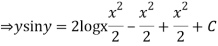
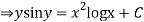
Question-3: Solve-
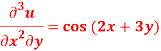
Sol.
Here we have-
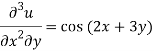
Integrate w.r.t. x, we get-
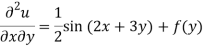
Integrate w.r.t. x, we get-
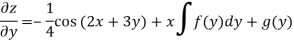
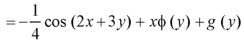
Integrate w.r.t. y, we get-
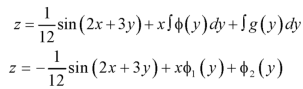
Question-4: Solve the differential equation-
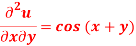
Given that  when y = 0, and u =
when y = 0, and u =  when x = 0.
when x = 0.
Sol.
We have-

Integrating partially w.r.t. y, we get-
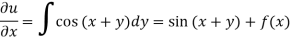
Now from the boundary conditions, 
Then-
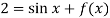
From which,
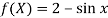
It means,
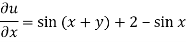
On integrating partially w.r.t. x givens-
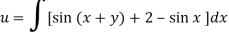
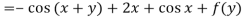
From the boundary conditions, u =  when x = 0
when x = 0

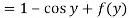
From which-

Therefore the solution of the given equation is-
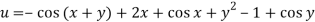
Question-5: Solve 
Solution. Rewriting the given equation as

The subsidiary equations are 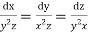
The first two fractions give 
Integrating we get 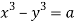 n (i)
n (i)
Again the first and third fraction give xdx = zdz
Integrating, we get 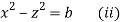
Hence from (i) and (ii), the complete solution is
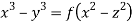
Question-6: Solve 
Solution. Here the subsidiary equations are 
Using multipliers x,y, and z we get each fraction = 
 which on integration gives
which on integration gives 
Again using multipliers l, m and n we get each fraction 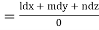
 which on integration gives lx +my +nz = b (ii)
which on integration gives lx +my +nz = b (ii)
Hence from (i) and (ii) the required solution is 
Question-7: Solve 
Solution. Here the subsidiary equations are 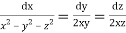
From the last two fractions, we have 
Which on integration gives log y = log z + log a or y/z=a (i)
Using multipliers x, y and z we have
Each fraction 
Which on integration gives 
Hence from (i) and (ii) the required solution is 
Question-8: Solve-
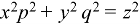
Sol.
This equation can be transformed as-

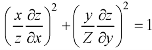
 ………. (1)
………. (1)
Let
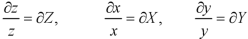
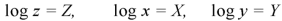
Equation (1) can be written as-
 ………… (2)
………… (2)
Let the required solution be-
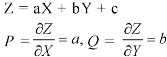
From (2) we have-

Question-9: Solve-
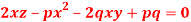
Sol.
Let
Charpit’s subsidiary equations are-
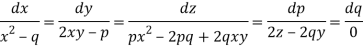
So that- dq = 0 or q = a
On putting q = a in (1) we get-
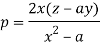
Such that-
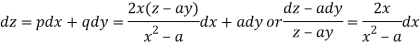
Integrating
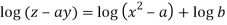
Or
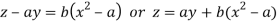
Which is the required solution.
Question-10: Solve-
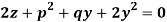
Sol.
Let

Charpit’s subsidiary equations are-

From the first and fourth ratios,
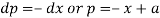
Substituting p = a – x in the given equation, we get-
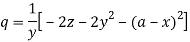
So that-
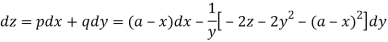
Multiply both sides by 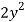 ,
,
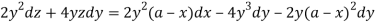
Integrating-
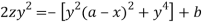
Or
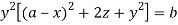
Which is the required solution.
UNIT-4
Partial differential equation: First order
Question-1: Find the differential equation of all circles touching the y-axis at the origin?
The equation of the circle that touches y-axis at the origin is
 ….(i)
….(i)
Differentiating (i) with respect to x, we get
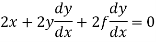
Or 
Or 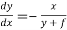
Or 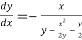
Or 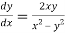
Or 
This is the required differential equation.
Question-2: Solve 
Solution. We have, 
Separating the variables we get
(sin y + y cos y )dy ={ x (2 log x +1} dx
Integrating both the sides we get 
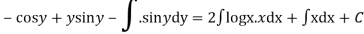
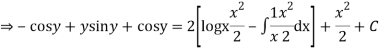

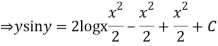
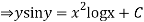
Question-3: Solve-
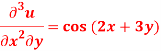
Sol.
Here we have-
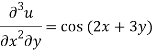
Integrate w.r.t. x, we get-

Integrate w.r.t. x, we get-
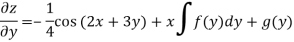
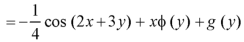
Integrate w.r.t. y, we get-
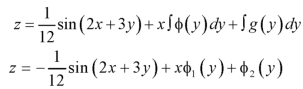
Question-4: Solve the differential equation-

Given that  when y = 0, and u =
when y = 0, and u =  when x = 0.
when x = 0.
Sol.
We have-

Integrating partially w.r.t. y, we get-
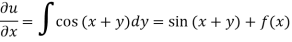
Now from the boundary conditions, 
Then-
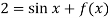
From which,

It means,
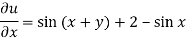
On integrating partially w.r.t. x givens-
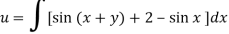
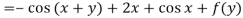
From the boundary conditions, u =  when x = 0
when x = 0

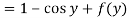
From which-
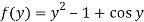
Therefore the solution of the given equation is-
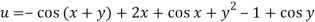
Question-5: Solve 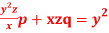
Solution. Rewriting the given equation as
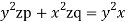
The subsidiary equations are 
The first two fractions give 
Integrating we get  n (i)
n (i)
Again the first and third fraction give xdx = zdz
Integrating, we get 
Hence from (i) and (ii), the complete solution is
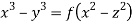
Question-6: Solve 
Solution. Here the subsidiary equations are 
Using multipliers x,y, and z we get each fraction = 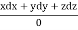
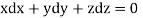 which on integration gives
which on integration gives 
Again using multipliers l, m and n we get each fraction 
 which on integration gives lx +my +nz = b (ii)
which on integration gives lx +my +nz = b (ii)
Hence from (i) and (ii) the required solution is 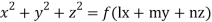
Question-7: Solve 
Solution. Here the subsidiary equations are 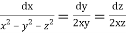
From the last two fractions, we have 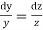
Which on integration gives log y = log z + log a or y/z=a (i)
Using multipliers x, y and z we have
Each fraction 
Which on integration gives 
Hence from (i) and (ii) the required solution is 
Question-8: Solve-

Sol.
This equation can be transformed as-
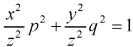
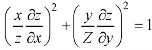
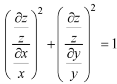 ………. (1)
………. (1)
Let
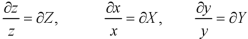
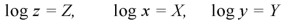
Equation (1) can be written as-
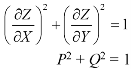 ………… (2)
………… (2)
Let the required solution be-
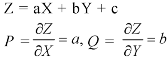
From (2) we have-
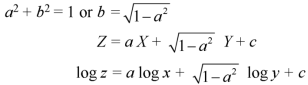
Question-9: Solve-
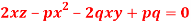
Sol.
Let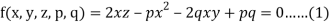
Charpit’s subsidiary equations are-
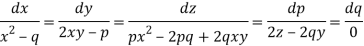
So that- dq = 0 or q = a
On putting q = a in (1) we get-
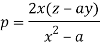
Such that-
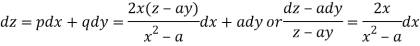
Integrating
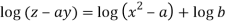
Or
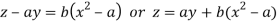
Which is the required solution.
Question-10: Solve-
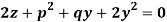
Sol.
Let
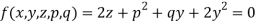
Charpit’s subsidiary equations are-

From the first and fourth ratios,
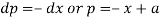
Substituting p = a – x in the given equation, we get-

So that-
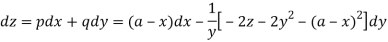
Multiply both sides by  ,
,
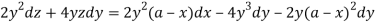
Integrating-
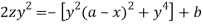
Or
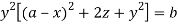
Which is the required solution.