Question Bank

UNIT 1

Introduction

Question 1) Comparison between Scalars and Vectors.

Answer:

Question 2) Given below is a list of quantities. Categorize each quantity as being either a vector or a scalar?

Answer:

Question 3) Aswan walks 10 m north, 12 m east, 3 m west and 5 m south and then stops to drink water. What is the magnitude of his displacement from his original point?

Answer: We know that displacement is a vector quantity hence the direction Aswan walks will either be positive or negative along an axis.

Now, to find the total distance travelled along the y-axis, let us consider the movement towards the north to be positive and the movement towards the south to be negative.

∑y=10m−5m=5m

He moved a net of 5 meters to the north along the y-axis.

Similarly, let us consider his movement towards the east to be positive and the movement towards the west to be negative.

∑y=−3m+12m=9m

He moved a net of 9 m to the east.

Using Pythagoras theorem, the resultant displacement can be found as follows:

D2= (∑x2)+(∑y2)

Substituting the values, we get

D2=(92)+(52) 

D2 = (106)2

√ D2 = √ (106)2

D=10.30m

Question 4) A laser beam is aimed 15.95° above the horizontal at a mirror 11,648 m away. It glances off the mirror and continues for an additional 8570. m at 11.44° above the horizon until it hits its target. What is the resultant displacement of the beam to the target?

Answer:

Let us break up the vector into their components –

Add vectors in the same direction with “ordinary” addition. –

Add vectors at right angles with a combination of pythagorean theorem for magnitude…

And tangent for direction.

Question 5) Draw the chart of fundamental units.

Answer:

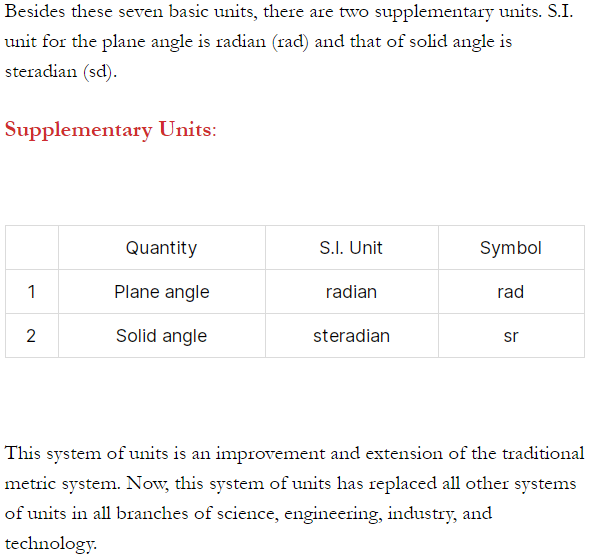
Question 6) Draw the chart of supplementary units?

Answer:

Question 7) Explain scalar and vectors.

Answer:

Scalars and vectors

In mechanics, as elsewhere, some quantities are scalar quantities and some are vector quantities. It is important to understand the difference between the two.

Scalars

Scalar quantities are quantities that only have a magnitude (size). Scalar quantities are useful, but for some quantities in mechanics we need more information; to this end we introduce vectors.

Vectors

Vector quantities are quantities that possess direction, as well as magnitude. Vectors are usually referred to in bold type

Question 8) Explain fundamental concept.

Answer:

Fundamental concept

Certain concepts and definitions are basic to the study of mechanics and they should be understood at the outset. The basic concepts in mechanics are space, time, mass and force. These concepts cannot be truly defined. They should be accepted on the basis of our intuition and experience, and used as a mental frame of reference for our study of mechanics.

In Newtonian mechanics, space, time and mass are absolute quantities, which mean that they are independent of each other (this is not true in RelativisticMechanics, where the time of an event depends upon its position and the mass of

a body varies with its velocity) and cannot be defined in terms of other quantities

Or in simpler terms. Force is a derived quantity.

Space: is the geometric region occupied by bodies whose positions are described by linear or angular measurements relative to a specific coordinate system. For three dimensional problems, three independent coordinates are needed. For two dimensional problems only two coordinates will be required.

Time: is a concept for measuring the succession and the duration of events. Time

Is not directly involved in the analysis of problems in Statics.

Mass: is a measure of the translational inertia of the body, which is its resistance

To a change in velocity. Mass can also be thought of as the quantity of matter in a

Body. The mass of a body affects the gravitational attraction force between it and other bodies. The concept of mass is used to characterize and compare two bodies on the basis of certain fundamental mechanical experiments depending on the definitions given above.

Question 9) Explain newton third law.

Answer:

Newton’s Third Law:

Each force (of “action”) has an equal and opposite force (of “reaction”)

Again, considering the boat of Fig. 2.1.3, the water exerts an upward buoyancy force on the boat, and the boat exerts an equal and opposite force on the water. This is illustrated

In Fig. 2.3d

.

Figure 2.1.4: Newton’s third law; (a) the water exerts a force on the

Boat, (b) the boat exerts an equal and opposite force on the water

Newton’s laws are used in the analysis of the most basic problems and in the analysis of the most advanced, complex, problems. They appear in many guises and sometimes they appear hidden, but they are always there in a Mechanics problem.

Question 10) Explain parallelogram law.

Answer:

1) The Parallelogram Law: Two vectors A and Btreated as free vectors, can be replaced by their equivalent R which is the diagonal of the parallelogram formed by A and B as its two sides, as shown. Ris called the resultant of A and B

Hence, the combined effect of two forces A and B (for example acting on a particle) is equivalent to the effect of their resultant.