Question Bank | unit 2 fundamental of statics

Back to Study material

Question Bank

UNIT 2

Fundamental of Static

Question 1)How much net force is required to accelerate a 1000 kg car at 4.00 m/s2?

Answer:

Solution:

Given,

a = 4.00 m/s2
m = 1000 kg

Therefore,

F = ma

= 1000 × 4

= 4000 N

Question 2) Aimee has a toy car of mass 2 kg. How much force should she apply on the car so that it should travel with the acceleration of 8 m/s2?

Answer:

Solution:

Known,

m (Mass of toy car) = 2 Kg,
a (Acceleration) = 8m/s2,

F is Force to be applied by aimmee = m × a

= 2 Kg × 8 m/s2 = 16 Kgm/s2 = 16 N.

Q.3) A hammer having a mass of 1 kg going with a speed of 6 m/s hits a wall and comes to rest in 0.1 sec. Compute the obstacle force that makes the hammer stop.

Answer:

Solution:

Given,

Mass of Hammer, m = 1 kg
Initial Velocity, u = 6 m/s
Final Velocity, v = 0 m/s
Time Taken, t = 0.1 s

The acceleration is: a = (v – u)/t

Therefore, a = -60 m/s2 [-ve sign indicates retardation]

Thus, the retarding Force, F = ma = 1 × 60 = 60 N

Question 4) What is the Line of Action of a Force?

Answer:

The line along which a force is acting on an object is called the line of action of the force. The point where the force is acting on an object is called the point of application of the force. The force which opposes the relative motion between the surfaces of two objects in contact and acts along the surfaces is called the force of friction.

Galileo experimentally proved that objects that are in motion move with constant speed when there is no force acting on it. He could note that when a sphere is rolling down an inclined plane, its speed increases because of the gravitational pull which is acting on it.

When all the forces acting on an object are balanced, the net force acting is zero. But, if all the forces acting on a body result in an unbalanced force, then the unbalanced force can accelerate the body, which means that a net force acting on a body can either change the magnitude of its velocity or change the direction of its velocity. For example, when many forces act on a body, and the body is found to be at rest, we can conclude that the net force acting on the body is zero.

Question 5) Two forces of 100 N & 150 N are acting simultaneously at a point. What is the resultant of these two forces, if the angle between them is 450.

Answer:

Given: P = 100 N

Q = 150 N

θ = 45o

R =? α=?

According to law of parallelogram of force,

R = √ P2 + Q2 + 2PQ Cos θ

R = √ 1002 + 1502 + 2 x 100 x 150 x Cos 450

R = 231.76 N

R ≈ 232 N - - - Ans - - - magnitude

Tanα = Q Sin θ / P + Q Cos θ

= 150 Sin 450 / 100 + 150 Cos 450

= 106.066 / 206.066

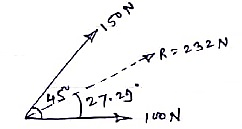Description: f1.jpg α = 27.290. . . . . Direction

Ans:

Question 6) The sum of two forces is 270 N & their resultant is 180 N. If Resultant is Perpendicular to P, find the two forces P & Q.

Answer:

Given:

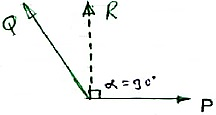Description: f1.jpg P + Q = 270 N

R = 180 N

α = 900

Soln:

Accr to law of parallelogram,

Tanα = Q Sin θ / P + Q Cos θ

Tan 90 = Q Sin θ / P + Q Cos θ

∞ = Q Sin θ / P + Q Cos θ

Here if P + Q Cos θ = 0, then only above term will become infinity.

Thus, P + Q Cosθ= 0

P = - Q Cos θ

-P = Q Cosθ . . . . (1)

Now, R2 = P2 + Q2 + 2PQ Cos θ

1802 = P2 + Q2 + 2P(-P) . . . from eqn (1)

1802 = P2 + Q2 + (-2P2)

1802 = P2 -2P2 + Q2

1802 = - P2 + Q2

1802 = Q2 - P2

1802 = (Q- P) (Q+ P)

= (Q- P) x 270

Q- P = 1802 / 270

Q- P = 120 . . . (ii)

& we know that

Q + P = 270 . . . (iii)

Solving (ii) & (iii) i.e. add eqn (ii) & (iii)

Q – P = 120

+ Q + P = 270

_______________

2Q + 0 = 390

2Q = 390

Q = 195 N & P = 75 N . . . Ans

Question 7)For two forces P & Q acting at a point. Maximum resultant is 2000 N and minimum magnitude of resultant is 800 N. Find values of P & Q.

Answer:

We know that,

R2 = P2 + Q2 + 2PQ Cos θ

For max value of R, Cos θ must be 1 i.e. Cos θ = 1

i.e. θ = 0, then only cosθ = 1

Rmax = √ P2 + Q2 + 2PQ Cos θ

= √ P2 + Q2 + 2PQ Cos 0

= √ P2 + Q2 + 2PQ

2000 = √ P2 + 2PQ + Q2

= √ (P + Q)2

2000 = P + Q . . . .Eqn (1)

Now for minimum value of R,

θ = 1800

Rmin= √ P2 + Q2 + 2PQ Cos θ

= √ P2 + Q2 + 2PQ Cos θ

= √ P2 + Q2 - 2PQ

= √ P2 - 2PQ+ Q2

= √ (P – Q)2

800 = P – Q . . . . . Eqn (ii)

Solving eqn (i) &eqn (ii) we get,

i.e. Add eqn (i) & (ii),

P + Q = 2000

- P - Q = 800

_______________

2P + 0 = 2800

P = 2800 / 2

P = 1400 N ….Ans

&P + Q = 2000

1400 + Q = 2000

Q = 600 N . . . Ans

Ans P = 1400 N

Q = 600 N

Question 8)The angle between the two forces P & Q is θ. If Q is doubled then new resultant is perpendicular to P. Prove that Q = R.

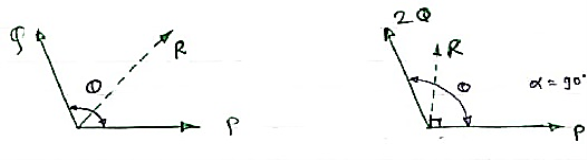
Answer:

R2 = P2 + Q2 + 2PQ Cos θ . . . (1)

Also tan 90 = Q Sin θ / P + Q Cos θ

∞ = 2Q Sin θ / P + (2Q) Cos θ= Q

If P + (2Q) Cos θ = 0 then only above term will be infinity.

P + (2Q) Cos θ = 0

-P = (2Q) Cos θ-- put in eqn (I)

R2 = P2 + Q2 + (P x (-P))

= P2 + Q2 - P2

R2 = P2

Taking sq. Root

R = P -- -Proved

Question 9)The angle betn the two concurrent forces is 900 & their resultant is 2500 N. The resultant makes an angle of 460 with one force. Determine magnitude of each force. PU – many 14 – 4m

Description: f1.jpg Answer:

By using, R2 = P2 + Q2 + 2PQ Cos θ

25002 = P2 + Q2 + 2PQ Cos 90

As cos 90 = 0 then

25002 = P2 + Q2 . . . (1)

Now,

Tanα = Q Sin θ / P + Q Cos θ = Q Sin 90 / P + Q Cos 90

Tanα = Q / P

Tan46 = Q / P

Q = 1.0355 P - - substitute in eqn (1)

25002 = P2 + [(1.0355)2 P2]

P2 = 3017537.93

P = 1737 N Q = 1798 N

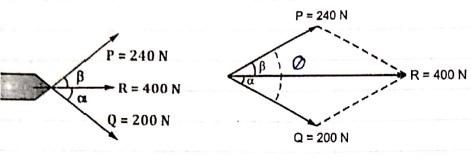Description: f1.jpg Question 10)Resultant force R = 400 N has two component forces P = 240 N and Q = 200 N as shown. Determine direction of component forces i.e. α and β w.r.t. Resultant force.