Unit – 2
Unit – 2
Partial differentiation
Q 1:
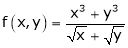
Solution: Consider 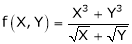
Put 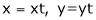
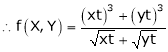

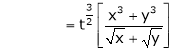
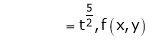 .
.
Thus degree of f(x, y) is 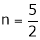
Note that
If  be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
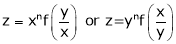
Q 2: Differentiate y = cos x2
Solution:
Given,
y = cos x2
Let u = x2, so that y = cos u
Therefore: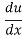 =2x
=2x
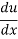 = -sin u
= -sin u
And so, the chain rule says:
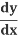 =
=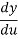 .
.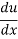
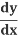 = -sin u × 2x
= -sin u × 2x
= -2x sin x2
Q 3:
Differentiate f(x)=(1+x2)5.
Solution:
Using the Chain rule,
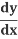 =
= 
Let us take y = u5 and u = 1+x2
Then 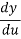 =
=  (u5) = 5u4
(u5) = 5u4
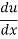 =
= 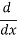 (1 + x2 )= 2x.
(1 + x2 )= 2x.
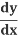 = 5u4⋅2x = 5(1+x2)4⋅2x
= 5u4⋅2x = 5(1+x2)4⋅2x
= 10x(1+x4)
Q 4: x2 + y2 = r2
Differentiate with respect to x:
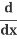 (x2) +
(x2) +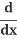 (y2) =
(y2) =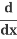 (r2)
(r2)
Let's solve each term:
Use the Power Rule: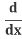 (x2) = 2x
(x2) = 2x
Use the Chain Rule (explained below): 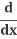 (y2) = 2y
(y2) = 2y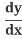
r2 is a constant, so its derivative is 0:d/dx(r2) = 0
Which gives us:
2x + 2y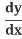 = 0
= 0
Collect all the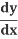 on one side
on one side
Y 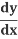 = −x
= −x
Solve for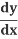 :
:
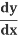 =-
=- 
The Chain Rule Using 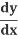 :
:
Let's look more closely at how 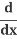 (y2) becomes 2y
(y2) becomes 2y 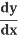
The Chain Rule says:
 =
=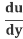 .
.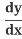
Substitute in u = y2:
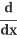 (y2) =
(y2) =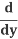 (y2) .
(y2) .
And then:
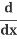 (y2) = 2y
(y2) = 2y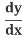
Basically, all we did was differentiate with respect to y and multiply by dy/dx
Example 2:
The following problems require the use of implicit differentiation. Implicit differentiation is nothing more than a special case of the well-known chain rule for derivatives. The majority of differentiation problems in first-year calculus involve functions y written EXPLICITLY as functions of x. For example, if
 ,
,
Then the derivative of y is
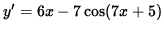 .
.
However, some functions y is written IMPLICITLY as functions of x. A familiar example of this is the equation
x2 + y2 = 25,
Which represents a circle of radius five cantered at the origin. Suppose that we wish to find the slope of the line tangent to the graph of this equation at the point (3, -4) .
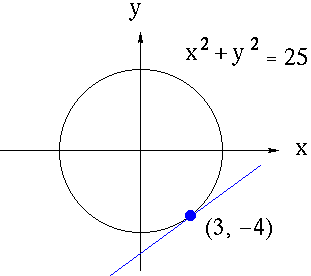
How could we find the derivative of y in this instance? One way is to first write y explicitly as a function of x. Thus,
x2 + y2 = 25,
y2 = 25 - x2,
And
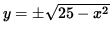 ,
,
Where the positive square root represents the top semi-circle and the negative square root represents the bottom semi-circle. Since the point
(3, -4) lies on the bottom semi-circle given by
 ,
,
The derivative of y is
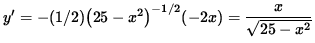 ,
,
i.e.,
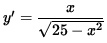 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
 .
.
Unfortunately, not every equation involving x and y can be solved explicitly for y . For the sake of illustration we will find the derivative of y WITHOUT writing y explicitly as a function of x . Recall that the derivative (D) of a function of x squared, (f(x))2 , can be found using the chain rule :
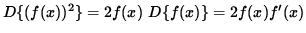 .
.
Since y symbolically represents a function of x, the derivative of y2 can be found in the same fashion :
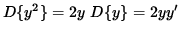 .
.
Now begin with
x2 + y2 = 25 .
Differentiate both sides of the equation, getting
D ( x2 + y2 ) = D ( 25 ) ,
D ( x2 ) + D ( y2 ) = D ( 25 ) ,
And
2x + 2 y y' = 0 ,
So that
2 y y' = - 2x ,
And
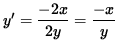 ,
,
i.e.,
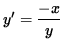 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
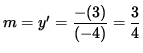
Q 5: Find the total differential of w=x3yz + x y +z +3 at (1,2,3)
Solution: The total differential at the point (x0, y0, z0) is
Dw = wx (x0, y0, z0). Dx +wy( x0,y0,z0).dy + wz ( x0,y0,z0).dz
In our case,
wx=3x2yz+y wy=x3z+x wz=x3y+1
Substituting in the point (1,2,3) we get
wx(1,2,3) =20
wy(1,2,3) =4
wz(1,2,3) =3
Thus, the total differential is.,
Dw = 20dx+4dy+3dz.
Unit – 2
Unit – 2
Partial differentiation
Q 1:
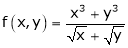
Solution: Consider 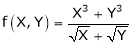
Put 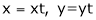

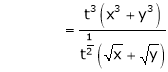
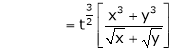
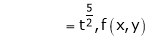 .
.
Thus degree of f(x, y) is 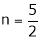
Note that
If 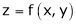 be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
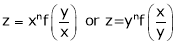
Q 2: Differentiate y = cos x2
Solution:
Given,
y = cos x2
Let u = x2, so that y = cos u
Therefore: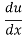 =2x
=2x
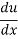 = -sin u
= -sin u
And so, the chain rule says:
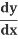 =
=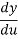 .
.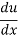
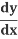 = -sin u × 2x
= -sin u × 2x
= -2x sin x2
Q 3:
Differentiate f(x)=(1+x2)5.
Solution:
Using the Chain rule,
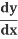 =
= 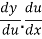
Let us take y = u5 and u = 1+x2
Then 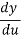 =
= 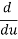 (u5) = 5u4
(u5) = 5u4
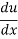 =
=  (1 + x2 )= 2x.
(1 + x2 )= 2x.
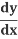 = 5u4⋅2x = 5(1+x2)4⋅2x
= 5u4⋅2x = 5(1+x2)4⋅2x
= 10x(1+x4)
Q 4: x2 + y2 = r2
Differentiate with respect to x:
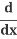 (x2) +
(x2) +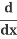 (y2) =
(y2) =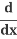 (r2)
(r2)
Let's solve each term:
Use the Power Rule: (x2) = 2x
(x2) = 2x
Use the Chain Rule (explained below): 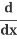 (y2) = 2y
(y2) = 2y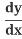
r2 is a constant, so its derivative is 0:d/dx(r2) = 0
Which gives us:
2x + 2y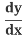 = 0
= 0
Collect all the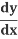 on one side
on one side
Y 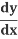 = −x
= −x
Solve for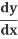 :
:
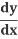 =-
=- 
The Chain Rule Using 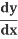 :
:
Let's look more closely at how 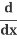 (y2) becomes 2y
(y2) becomes 2y 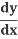
The Chain Rule says:
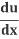 =
= .
.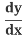
Substitute in u = y2:
 (y2) =
(y2) =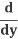 (y2) .
(y2) .
And then:
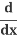 (y2) = 2y
(y2) = 2y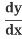
Basically, all we did was differentiate with respect to y and multiply by dy/dx
Example 2:
The following problems require the use of implicit differentiation. Implicit differentiation is nothing more than a special case of the well-known chain rule for derivatives. The majority of differentiation problems in first-year calculus involve functions y written EXPLICITLY as functions of x. For example, if
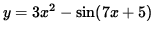 ,
,
Then the derivative of y is
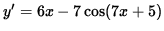 .
.
However, some functions y is written IMPLICITLY as functions of x. A familiar example of this is the equation
x2 + y2 = 25,
Which represents a circle of radius five cantered at the origin. Suppose that we wish to find the slope of the line tangent to the graph of this equation at the point (3, -4) .

How could we find the derivative of y in this instance? One way is to first write y explicitly as a function of x. Thus,
x2 + y2 = 25,
y2 = 25 - x2,
And
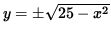 ,
,
Where the positive square root represents the top semi-circle and the negative square root represents the bottom semi-circle. Since the point
(3, -4) lies on the bottom semi-circle given by
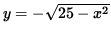 ,
,
The derivative of y is
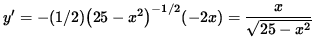 ,
,
i.e.,
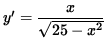 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
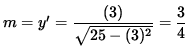 .
.
Unfortunately, not every equation involving x and y can be solved explicitly for y . For the sake of illustration we will find the derivative of y WITHOUT writing y explicitly as a function of x . Recall that the derivative (D) of a function of x squared, (f(x))2 , can be found using the chain rule :
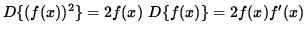 .
.
Since y symbolically represents a function of x, the derivative of y2 can be found in the same fashion :
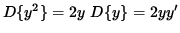 .
.
Now begin with
x2 + y2 = 25 .
Differentiate both sides of the equation, getting
D ( x2 + y2 ) = D ( 25 ) ,
D ( x2 ) + D ( y2 ) = D ( 25 ) ,
And
2x + 2 y y' = 0 ,
So that
2 y y' = - 2x ,
And
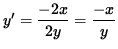 ,
,
i.e.,
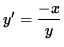 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
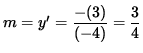
Q 5: Find the total differential of w=x3yz + x y +z +3 at (1,2,3)
Solution: The total differential at the point (x0, y0, z0) is
Dw = wx (x0, y0, z0). Dx +wy( x0,y0,z0).dy + wz ( x0,y0,z0).dz
In our case,
wx=3x2yz+y wy=x3z+x wz=x3y+1
Substituting in the point (1,2,3) we get
wx(1,2,3) =20
wy(1,2,3) =4
wz(1,2,3) =3
Thus, the total differential is.,
Dw = 20dx+4dy+3dz.