Question Bank

Unit - 2

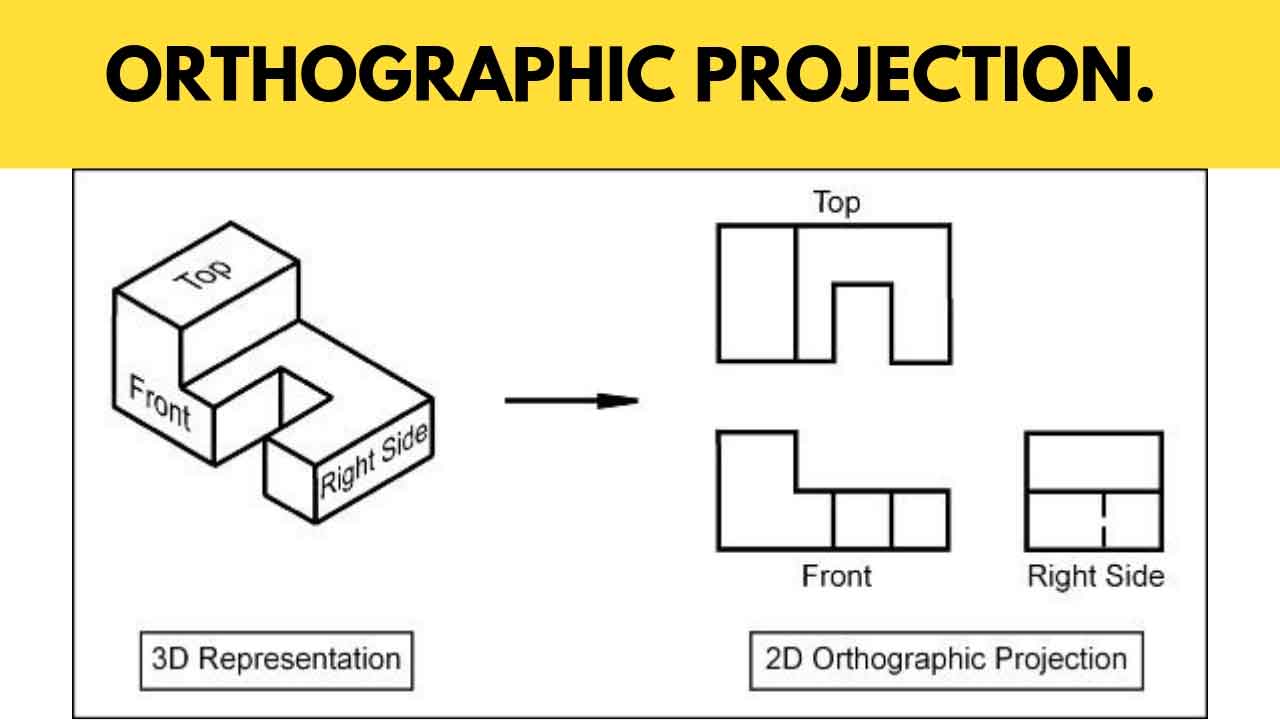
1. Explain first angle projection method.

Ans:

If the object to be situated in front of the V.P. And above the H.P. i.e. in the first quadrant and then projected on to the planes. This method of projection is known as first-angle projection method. The object lies between the observer and the plane of projection. In this method, when the views are drawn in their relative positions, the top view comes below the front view. In other words, the view seen from above is placed on the other side of (i.e. below) the front view. Each projection shows the view of that surface (of the object) which is remote from the plane on which it is projected, and which is nearest to the observer.

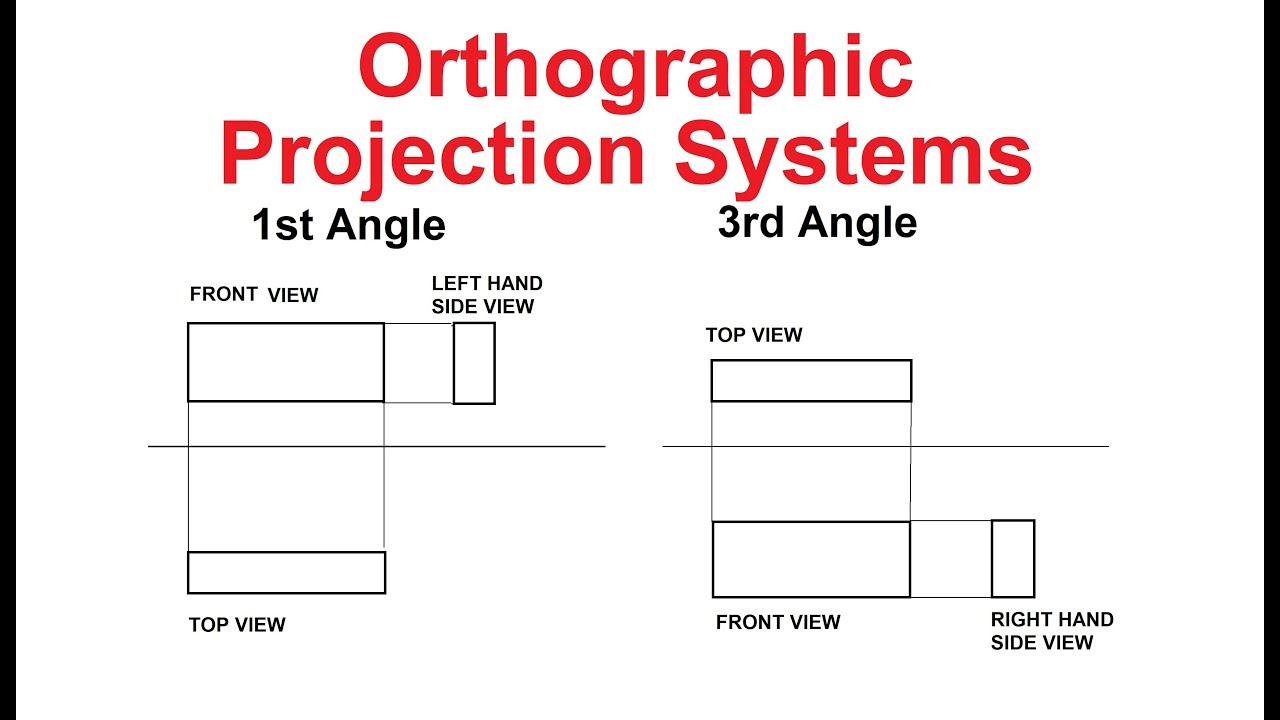
2.     Explain Third angle projection method.

Ans:

In this method of projection, the object is assumed to be situated in the third quadrant [fig.]. The planes of projection are assumed to be transparent. They lie between the object and the observer. When the observer views the object from the front, the rays of sight intersect the V.P. The figure formed by joining the points of intersection in correct sequence is the front view of the object. The top view is obtained in a similar manner by looking from above. When the two planes are brought in line with each other, the views will be shown in fig. The top view in this case comes above the front view.

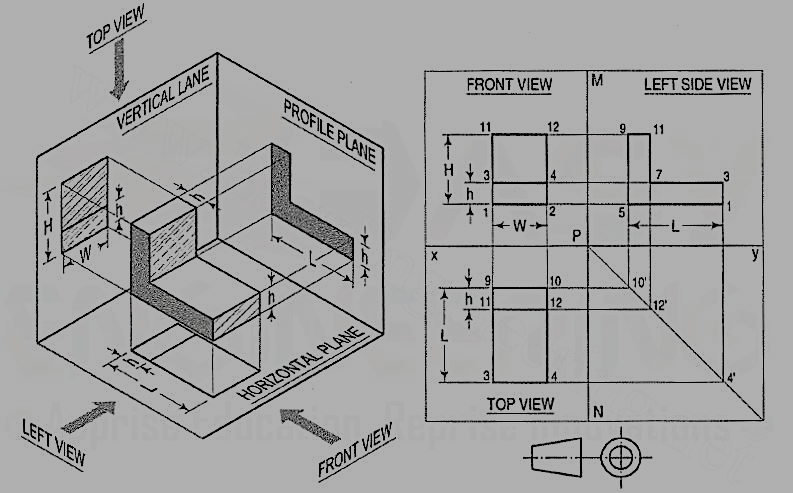
3.     A L-shaped solid object having dimensions of length (L), width (W) and height (H). If this object is lying in the first quadrant. Draw its front view, top view and side view.

Steps:

(i) Mark the visible corners of the given block as shown front view: Assume that you are viewing the object in the direction of the arrow towards the imaginary V.P. What you will see is a rectangle of height (H) and width (W) on V.P. This will be the front view. To draw this view:

(ii) Draw a reference line xy, which represents the intersecting line of the planes V.P. And H.P. Draw a rectangle as shown W and H, above xy make sure that the width is parallel to the Iinexy. The rectangle is the front orthogonal view of the object.

(iii) Draw a line parallel to and thickness of h to the line 1-2. The rectangle 1-2-4-3 is the front view of the horizontal L-shaped stem of the object.

4.     Explain projection of lines parallel to one or both planes.

Ans -

Line Parallel to one or both the planes:

(a) Line AB is parallel to the H.P.

a and b are the top views of the ends A and B respectively. It can beclearly seen that the figure ABba is a rectangle. Hence, the top view ab isequal to AB.a'b' is the front view of AB and is parallel to xy.

(b) Line CD is parallel to the V.P.

The line c'd' is the front view and is equal to CD; the top view cd isparallel to xy.

(c) Line ff is parallel to the H.P. And the V.P.

Ef is the top view and e'f' is the front view; both are equal to ff andparallel to xy.

Hence, when a line is parallel to a plane, its projection on that plane is equal to itstrue length, while its projection on the other plane is parallel to the reference line.

5.     Explain line inclined to both the planes.

Ans –

(a) A line AB (fig. 4) is inclined at θ to the H.P. And is parallel to the V.P. The end A is in the H.P. AB is shown as the hypotenuse of a right-angled triangle, making the angle θ with the base.

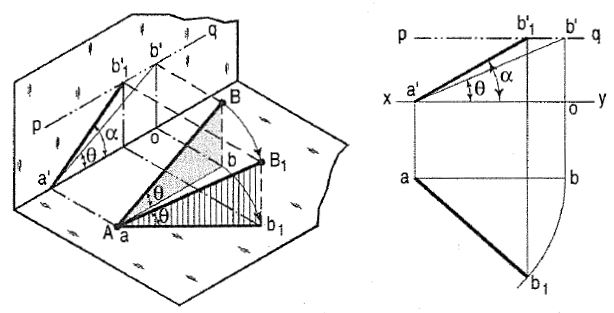
Figure 4

The top view ab is shorter than AB and parallel to xy. The front view a'b' is equal to AB and makes the angle θ with xy.

Keeping the end, A fixed and the angle θ with the H.P. Constant, if the end B is moved to any position, say B1, the line becomes inclined to the V.P. Also.

In the top view, b will move along an arc, drawn with a as centre and ab as radius, to a position b1. The new top view ab1 is equal to ab but shorter than AB.

In the front view, b' will move to a point b'1 keeping its distance from xy constant and equal to b'o; i.e. it will move along the line pq, drawn through b' and parallel to xy. This line pq is the locus or path of the end 8 in the front view. b'1 will lie on the projector through b1• The new front view a'b'1 is shorter than a'b' (i.e. AB) and makes an angle a with xy. A is greater than θ.

Thus, if the inclination θ of AB with the H.P. Is constant, even when it is inclined to the V.P.

(i) its length in the top view, viz. Ab remains constant; and

(ii) the distance between the paths of its ends in the front view, viz. b'o remains constant.

(b) The same line AB (fig. 5) is inclined at θ to the V.P. And is parallel to the H.P. Its end A is in the V.P. AB is shown as the hypotenuse of a right-angled triangle making the angle θ with the base.

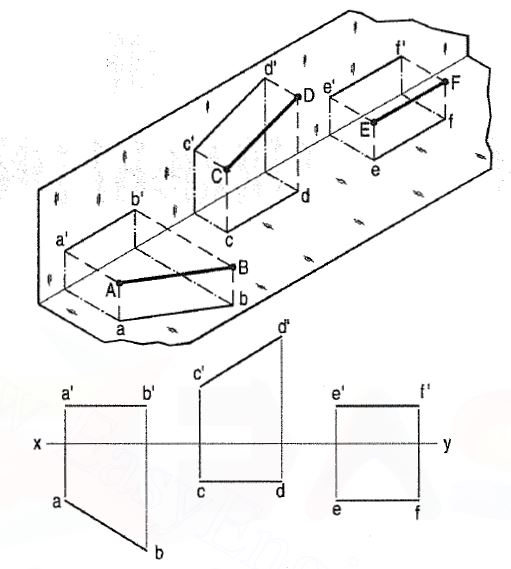
Figure 5