Question Bank
Unit - 8
- What are various methods of development of surfaces?
Ans:
1. Parallel-line development:
It is employed in case ofprisms and cylinders in whichstretch-out-line principle isused. Lines A-A and A1-A1in fig.2 are called thestretch-out Iines.
2. Radial-line development:
Itis used for pyramids andcones in which the truelength of the slant edge orthe generator is used as radius.
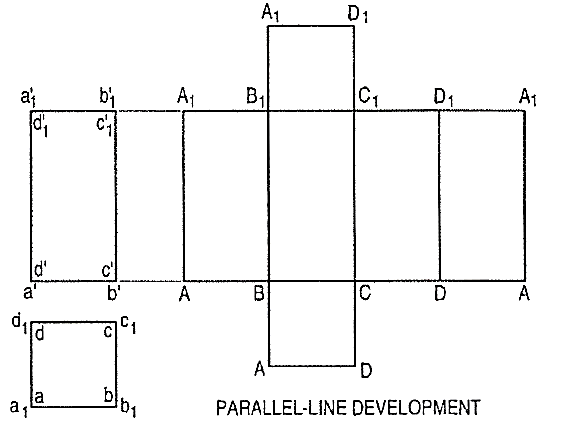
Figure 2
3. Triangulation development:
This is used to develop transition pieces. This is simply a method of dividing a surface into many triangles and transferring them into the development.
4. Approximate method:
It is used to develop objects of double curved orwarped surfaces as sphere, paraboloid, ellipsoid, hyperboloid and helicoid.
2. Draw the development of the surface of the part P of the cube,the front view of which is shown in fig. 3(i).Name all the corners of the cube and the points at which the edges are cut.
(i) Draw the stretch-out lines A-A and E-E directly in line with the front view, andassuming the cube to be whole, draw four squares for the vertical faces, onesquare for the top and another for the bottom as shown in fig. 3(ii).
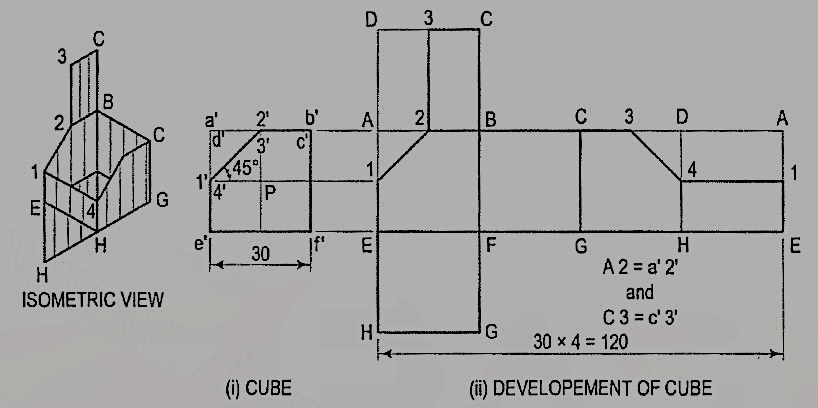
Figure 3
(ii) Name all the corners. Draw a horizontal line through 1' to cut AE at 1 andDH at 4. a' b' is the true length of the edge. Hence, mark a point 2 onAB and 3 on CD such that A 2 = a' 2' and C 3 = c' 3'. Mark the point3 on CD in the top square also.
(iii) Draw lines 1-2, 2-3, 3-4 and 4-1, and complete the development as shown.Keep lines for the removed portion, viz. A1, A2, 3D, D4 and DA thin and fainter.
3. Draw the development of the lateral surface of the part P of the pentagonal prism shown in fig. 3 (i).

Figure 5
Name the corners of the prism and the points at which the edges are cut.
(i) Draw the development assuming the prism to be whole [fig. 5(ii)].It is made up of five equal rectangles.
(ii) Draw horizontal lines through points 1’, 2’ etc. to cut the lines for the corresponding edges in the development at points 1, 2 etc.
(iii)Draw lines joining these points and complete the development as shown.
4. Draw the development of the lateral surface of the part P of the hexagonal prism shown in fig. 6 (i).
Name the points at which the edges are cut and draw the developmentassuming the prism to be whole [fig. 6(ii)].
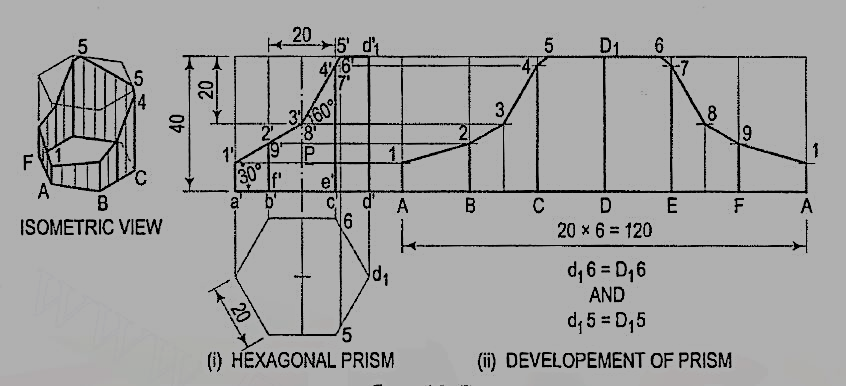
Figure 6
(i) Obtain all the points except 5 and 6 by drawing horizontal lines. Note thatpoints 3 and 8 lie on vertical lines drawn through the mid-points of BC and EF.
(ii) Mark points 5 and 6 such that SD1 = 5d1 and D16 = d16.
(iii) Draw lines joining points 1, 2, 3 etc. in correct sequence and complete therequired development as shown.
5. Draw the development of the lateral surface of the part P ofthe triangular pyramid shown in fig. 8 (i). The line o'1' in the front view is thetrue length of the slant edge because it is parallel to xy in the lop view. The truelength of the side of the base is seen in the top view.
(i) Draw the development of the lateral surface of the whole pyramid [fig. 8(ii)]as explained above. On 01 mark a point A such that OA = o'a'. o'2' (withwhich o'3' coincides) is not the true length of the slant edge.
(ii) Hence, through b', draw a line parallel to the base and cutting o' a' at b".o'b" is the true length of o'b' as well as o'c'. Mark a point B in 02 andC in 03 such that OB = OC = o'b".
(iii) Draw lines AB, BC and CA and complete the required development as shown.Keep the arc and the lines for the removed part fainter.

Figure 8
6. Draw the development of the lateral surface of the frustum ofthe square pyramid shown in fig. 9 (i).
(i) Determine the position of the apex. None of the lines in the front viewshow’s the true length of the slant edge. Therefore, draw the top view andmake any one line (for the slant edge) horizontal, i.e. parallel to xy anddetermine the true length o'1 '1. Through a', draw a line parallel to the baseand obtain the true length o'a".
(ii) With O as centre and radius o'1 '1, draw an arc and obtain the developmentof the lateral surface of the whole pyramid [fig. 9(ii)].
(iii) With centre O and radius o' a", draw an arc cutting O1, O2 etc. at pointsA, B etc. respectively.
(iv) Draw lines AB, BC, CD and DA and complete the required development.Note that these lines are respectively parallel to lines 1-2, 2-3 etc.
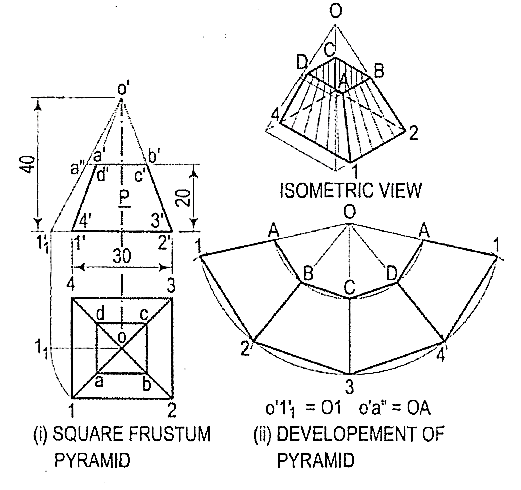
Figure 9
7. Draw the development of the lateral surface of the truncatedcone shown in fig. 11 (i).
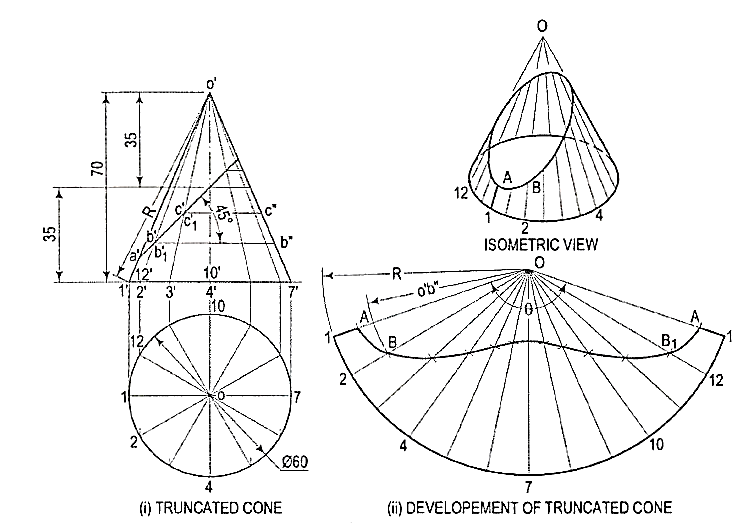
Figure 11
Assuming the cone to be whole, let us draw its development.
(i) Draw the base-circle in the top view and divide it into twelve equal parts.
(ii) With any point O as centre and radius equal to o'1' or o'7', draw an arcof the circle [fig. 15-24(ii)]. The length of this arc should be equal to thecircumference of the base circle. This can be determined in two ways.
(iii) Calculate the subtended angle θ by the formula,
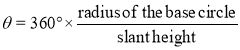
Cut-off the arc so that it subtends the angle θ at the center and divide itinto twelve equal parts.
(iv) Step-off with a bow-divider, twelve equal divisions on the arc, each equalto one of the divisions of the base-circle.
(This will give an approximate length of the circumference. Note thatthe base-circle should not be divided into less than twelve equal parts.)
(v) Join the division-points with 0, thus completing the development of thewhole cone with twelve generators shown in it [fig. ,11(ii)].
(vi) The truncated portion of the cone may be deducted from this development bymarking the positions of points at which generators are cut and then drawinga curve through them. For example, generators o'2' and o'12' in the front vieware cut at points b' and b'1 which coincide with each other. The true length ofo' b' may be obtained by drawing a line through b', parallel to the base andcutting o'7' at b". Then o'b" is the true length of o'b'.
(vii) Mark points B and 81 on generators 02 and 0-12 respectively, such thatOB = 0B1 = o' b". Locate all points in the same way and draw a smoothcurve through them. The figure enclosed this curve and the arc is thedevelopment of the truncated cone.
8. In air-conditioning system a rectangular duct of 100 mm x 50 mmconnects another rectangular duct of 50 mm x 25 mm through the transition pieceas shown in fig. 14(i). Neglecting thickness of a metal sheet, develop the lateralsurface of the transition piece as shown in fig. 14(ii).
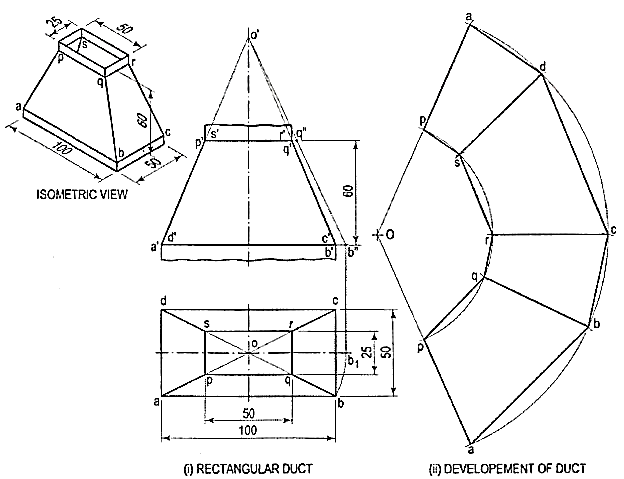
Figure 14
The transition piece is a frustum of a rectangular pyramid.
(i) Determine the position of the apex of the pyramid by extending a'p' and b'q'as shown. None of the lines in the front view shows the true length of theslant edge. Therefore, draw the top view and make any slant line parallel toxy and determine its true length o'b".
(ii) With O as centre and radius o'b", draw an arc and obtain the development ofa whole pyramid as shown.
(iii) With Oascentre and radius o'q", draw an arc cutting oa, ob, oc at points p, q, etc.respectively. Join them in sequence and complete the development as shown.