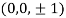Unit – 3
Unit – 3
Applications of Partial differentiation
Q 1: Find the equation of the tangent to the curve 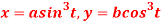 at the point
at the point  ?
?
Solution: Given Curve 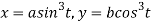
Differentiating both side with respect to t.
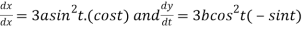
By Chain Rule 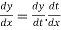
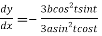
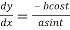
Therefore, the equation of the tangent
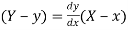
Or  …(i)
…(i)
At the point 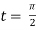
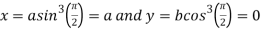
Also 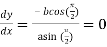
Substituting all these values in (i) we get

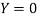
Hence the equation of the tangent is  .
.
Q 2: At what point is the tangent to the curve  parallel to the chord joining the points (0,0) and (0,1).
parallel to the chord joining the points (0,0) and (0,1).
Solution: Given curve is 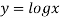
Equation of the chord joining the points (0,0) and (0,1) is
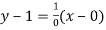
Or 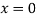 i.e. Parallel toY-axis …(i)
i.e. Parallel toY-axis …(i)
Given curve is 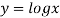
Differentiating both side with respect to x.
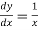
Equation of tangent parallel to Y-axis is 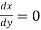
Or 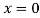 (as above)
(as above)
Since curve is 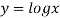
At 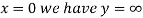 (ii)
(ii)
From (i) and (ii) we conclude that the point tangent parallel to the chord is 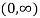 .
.
Hence the point tangent parallel to the chord is  .
.
Q 3: Prove that 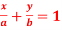 touches the curve
touches the curve  at the point where the curve crosses the axis of y.
at the point where the curve crosses the axis of y.
Solution: Given curve is 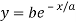
It will cross the y-axis at x=0, we get
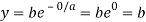
Hence the point of the curve on the Y-axis is 
Since curve is 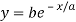
Differentiating both side with respect to x, we get
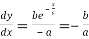
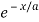 .
.
At point (0, b) we have 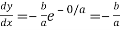 …(i)
…(i)
Again given 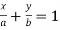
Differentiating both side with respect to x, we get
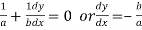
Again at the point (0, b) we have 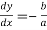 …..(ii)
…..(ii)
As we know that two curve touches each other then they have Same Lope at the point of intersection.
From (i) and (ii) we conclude that both the curve touches each other on Y-axis.
Q 4: Find the equation of the normal of the curve 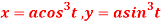 at
at .
.
Solution: Given curve 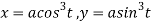
Differentiating both side with respect to t.
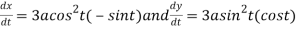
By Chain Rule 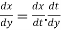
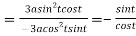
At the point 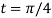 ,
,
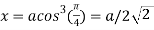

Also 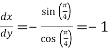
Therefore, equation of the normal at 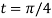

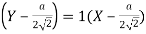
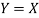
Hence the equation of the normal at 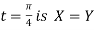 .
.
Q 5: Prove that the curve 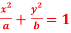 and
and  will cut orthogonally if
will cut orthogonally if 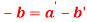 ?
?
Solution: Given curves 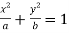 …(i)
…(i)
And  …(ii)
…(ii)
Let 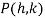 be a intersection point of curve (i) and (ii)
be a intersection point of curve (i) and (ii)
Then 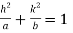
And 
On solving we get
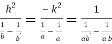
Or 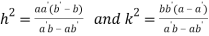 …(iii)
…(iii)
Differentiating (i) with respect to x.
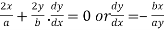
At the point 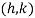 slope of (i) is given by
slope of (i) is given by 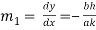
Differentiating (ii) with respect to x.
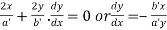
At the point  slope of (ii) is given by
slope of (ii) is given by 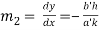
For orthogonal intersection, we have 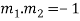
Substituting the values of slopes we get,
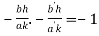
Or 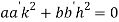
Putting values from (iii) we get
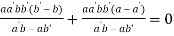
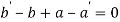
Or 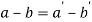
Hence proved.
Q 6: Find the lengths of the tangent, normal, sub tangent and subnormal for the cycloid:
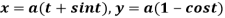
Solution: The equation of the cycloid 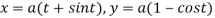
Differentiating both with respect to t .

By Chain Rule
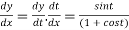
Length of tangent is 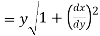
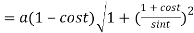
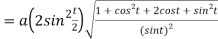
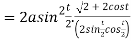

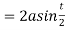
Length of normal is 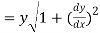
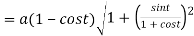
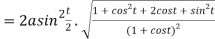
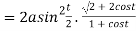
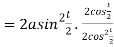

Length of sub tangent =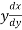
=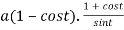
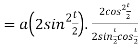
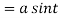
Length of sub normal =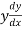
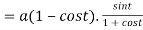
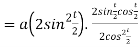
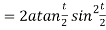
Q 7: Find out the maxima and minima of the function
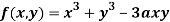
Solution: Given 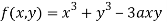 …(i)
…(i)
Partially differentiating (i) with respect to x we get
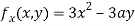 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
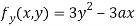 ….(iii)
….(iii)
Now, form the equations 
Using (ii) and (iii) we get
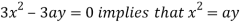
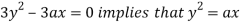
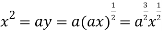 using above two equations
using above two equations
Squaring both side we get
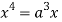
Or 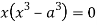
This show that 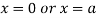
Also we get 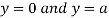
Thus we get the pair of value as 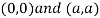
Now, we calculate
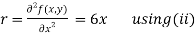
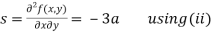

Putting above values in
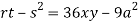
At point (0,0) we get

So, the point (0,0) is a saddle point.
At point 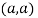 we get
we get
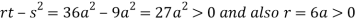
So the point 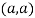 is the minimum point where
is the minimum point where 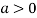
In case 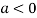
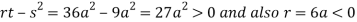
So the point 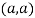 is the maximum point where
is the maximum point where 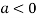
Q 8: Find the maximum and minimum point of the function
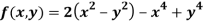
Solution: Partially differentiating given equation with respect to and x and y then equate them to zero
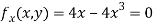
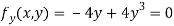
On solving above we get 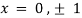
Also 
Thus, we get the pair of values (0,0), (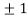 ,0) and (0,
,0) and (0,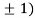
Now, we calculate

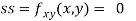
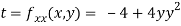
At the point (0,0)
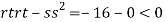
So function has saddle point at (0,0).
At the point (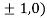
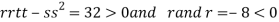
So the function has maxima at this point (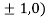 .
.
At the point (0,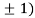
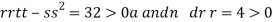
So the function has minima at this point (0,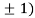 .
.
At the point (
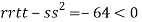
So the function has an saddle point at (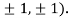
Q 9: Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Solution: Let first number be x, second be y and third be z.
According to the question
Let the given function be f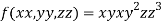
And the relation 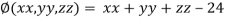
By Lagrange’s Method
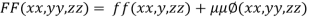
 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
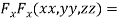
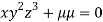 ….(ii)
….(ii)
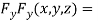
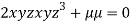 ….(iii)
….(iii)
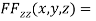
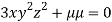 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
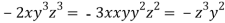
On solving
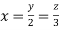
Putting it in given relation we get
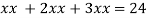
Or 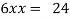
Or 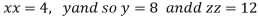
Thus, the first number is 4 second is 8 and third is 12
Q 10: The temperature T at any point 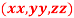 in space is
in space is 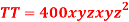 .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Solution: Given function is 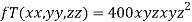
On the surface of unit sphere given 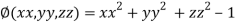 [
[ is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
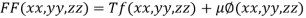
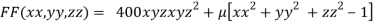 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
 or
or 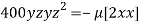 …(ii)
…(ii)
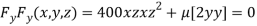 or
or 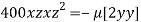 …(iii)
…(iii)
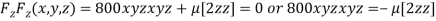 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get

Using given relation 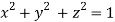
Or 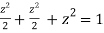
Or 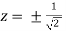
So that 
Or 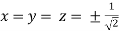
Thus, points are 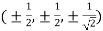
The maximum temperature is 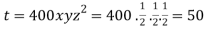
Q 11: If 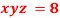 ,Find the value of x and y for which
,Find the value of x and y for which 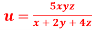 is maximum.
is maximum.
Solution: Given function is 
And relation is 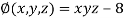
By Lagrange’s Method
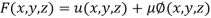
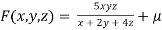 [
[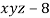 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
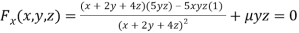
Or 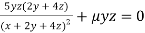 …(ii)
…(ii)
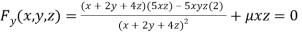
Or  …(iii)
…(iii)
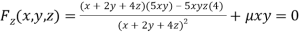
Or 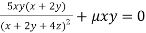 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
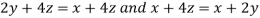
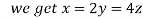
Using the given relation we get 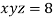
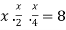
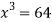
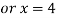
So that 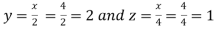
Thus, the point for the maximum value of the given function is 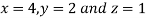
Q 12: Find the points on the surface 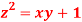 nearest to the origin.
nearest to the origin.
Solution: Let 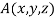 be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin 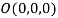 is
is
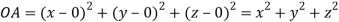
Thus, the given equation will be
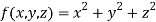
And relation is 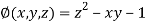
By Lagrange’s Method
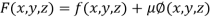
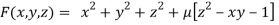 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
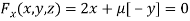
Or 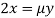 …(ii)
…(ii)
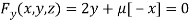
Or 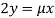 …(iii)
…(iii)
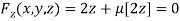
Or 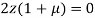
Or 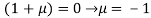
On solving equation (ii) by (iii) we get
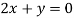
And 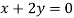
On subtracting we get 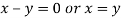
Putting in above 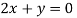
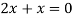
Or 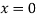
Thus 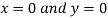
Using the given relation, we get
 = 0.0 +1=1
= 0.0 +1=1
Or 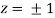
Thus, point on the surface nearest to the origin is